|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bourbaki N. — Algebra I: Chapters 1-3 |
|
|
 |
| Предметный указатель |
Direct decomposition of a ring I § no.
Direct factor I §4 no.
Direct limit Limit direct
Direct product I § no.
Direct product, internal I § no.
Direct sum I § no.
Direct system System direct
Direction of an affine linear variety II § no.
Direction parameters of an affine line II § no.
Direction vector of an affine line II § no.
Discriminant ideal of an algebra III § no.
Discriminant of a finite sequence in an algebra III § no.
Distributive (mapping) with respect to an index I § no.
Distributive action I § no.
Distributive, left distributive, right distributive, law I § no.
Distributivity of one law of composition with respect to another I § no.
Divisor of zero, left, right I § no.
Divisor, left, right I § no.
Domain, integral, domain of integrity I § no.
Double coset with respect to two subgroups I § no.
Dual bases II § nos.
Dual numbers, algebra of III § no.
Dual of a module II § no.
Dual, graded, of a graded module II § no.
Element centralizing a subset I § no.
Element derived from an element of the free algebra by substituting elements for indeterminates III § no.
Element derived from an element of the free associative algebra by substituting elements for indeterminates III § no.
Element invariant under an operator I § no.
Element normalizing a subset i § no.
Element resulting from substituting elements for indeterminates in a free group I § no.
Element, central I § no.
Element, free, of a module II § no.
Element, homogeneous (homogeneous of degree n), of a graded group II §11 no.
Element, identity I § no.
Element, isobaric, of a graded group II § no.
Element, left cancellable, right cancellable, cancellable I § no.
Element, left invertible, right invertible, invertible I § no.
Element, left regular, right regular, regular I § no.
Element, p-regular I § Exercise
Element, p-unipotent I § Exercise
Element, primitive, in a free group I § Exercise
Element, primitive, of a graded bigebra III § no.
Element, s-neighbouring I § Exercise
Element, torsion, of a module II § no.
Element, unit I §2 no.
Element, unit, of an algebra III § no.
Element, zero I § no.
Elements congruent modulo an ideal I § no.
Elements, conjugate, in a group I § no.
Elements, conjugate, under the operation of a group I § no.
Elements, diagonal, of a square matrix II § no.
Elements, linearly dependent (linearly independent) in a module II § no.
Elements, orthogonal II § no.
Elements, permutable, elements which commute I § no.
Empty matrix II § no.
Endomorphism I § no.
Endomorphism of a module II § no.
Endomorphism of a ring I § no.
Endomorphism, unimodular III § no.
Endomorphisms, equivalent, similar III § Exercise
Ends, number of ends I § Exercise
Envelope, injective, of a module II § no.
Equation of a hyperplane II § no.
Equation, linear, homogeneous linear equation, homogeneous linear equation associated with a linear equation II § no.
Equation, scalar linear II §2 no.
Equations (system of) of a vector subspace II § no.
Equations, linear (system of) II § no.
Equivalent composition series I § no.
Equivalent endomorphisms III §8 Exercise
Equivalent matrices II § no.
Even permutation I § no.
Exact diagram II § no.
Exact sequence II § no.
Expansion by a column III § no.
Expansion by a row III § no.
Expansion, Laplace III § no.
Extension of laws of operation I § no.
Extension of one group by another I § no.
Extension of one module by another II § no.
Extension of scalars (algebra obtained by) III § no.
Extension of scalars (module obtained by) II § no.
Extension, Cayley, of an algebra III § no.
Extension, central I § no.
Extension, essential, of a module II § Exercise
Extension, trivial I § no.
Extension, trivial, of a module II § no.
Exterior algebra of a module III § no.
Exterior power, p-th, of a matrix III § no.
Exterior power, p-th, of a module III § no.
Exterior power, p-th, of an endomorphism III § no.
Exterior product of p-vector and a q-vector III § no.
External law of composition I § no.
Factor of a product I § no.
Factor, direct, of a group I § no.
Factor, direct, of a module II § no.
Factors, system of III § Exercise
Faithful module III § no.
Faithfully (monoid operating) I § no.
Family, affinely free, affinely related, of points in an affine space II §9 no.
Family, basic, free, generating, in a group I § no.
Family, free, related, of elements of a module II § no.
Family, generating, of an algebra III § no.
Family, orthogonal, of projectors II § no.
Family, projectively free, projectively related, of points in a projective space II § no.
Fibre product I § no.
Field I §9 no.
Field of fractions of an integral domain I § no.
Field of left fractions I § Exercise
Field of rational numbers I § no.
Field, commutative, skew field I § no.
Field, projective II § no.
Finer composition series I § no.
Finite group I § no.
Finitely generated group I § Exercise
Finitely generated module II § no.
Fixer of a subset of a set I § no.
Fixing a subset of a set (operator, set of operators) I § no.
Form, canonical bilinear II § no.
Form, coordinate II § no.
Form, linear II § no.
Form, n-linear II § no.
Formula, binomial I § no.
Formula, Leibniz III § no.
Formulae of change of coordinates II § no.
Formulae, Cramer's III § no.
Formulae, transitivity, of norms and traces III §9 no.
Fractions (field of) of an integral domain I § no.
Fractions, group of, of a monoid I § no.
Fractions, monoid of, with denominators in S I § no.
Fractions, ring of, with denominators in S I § no.
Fractions, total ring of I § no.
Free algebra of a module III § Exercise
Free algebra, associative algebra, associative and commutative algebra III § no.
Free commutative group I § no.
Free commutative monoid I § no.
Free element, family, module, subset, system II § no. § no.
Free family in a group I § no.
Free group I § no.
Free magma I § no.
Free monoid I § no.
Free product of algebras III § Exercise
Free product of groups I § no.
Free vector in an affine space II § no.
Freely, group operating I § no.
Function, linearly affine, affine function II § no.
G-mean I § Exercise
G-set, homogeneous (G a group of operators) I § no.
G-set, homogeneous principal, homogeneous principal set under G I § no.
G-sets, weakly equivalent I § Exercise
Generated by a family of ordered pairs (equivalent relation) I § no.
| Generated by a subset (ideal) I § no. and § no.
Generated by a subset (stable subgroup) I § no.
Generated by a subset (stable subset) I § no.
Generated by a subset (subalgebra) III § no.
Generated by a subset (subfield) I § no.
Generated by a subset (submagma) I § no.
Generated by a subset (subring) I § no.
Generated by a subset (unital submagma, submonoid) I § no.
Generating family of a group I § no.
Generating family of an algebra III § no.
Generating set, system, of a field I § no.
Generating set, system, of a magma I § no.
Generating set, system, of a module II § no.
Generating set, system, of a ring I § no.
Generating set, system, of a stable subgroup I § no.
Generating set, system, of a stable subset I § no.
Generating set, system, of a unital submagma, of a submonoid I § no.
Generating set, system, of an ideal I § no.
Generators of a presentation I § no.
Graded algebra over a graded ring III § no.
Graded bigebra III § no.
Graded bigebra, skew III § no.
Graded cogebra III § no.
Graded group, module, ring II § nos.
Graded homomorphism II § no.
Graded subalgebra III § no.
Graded subring, submodule, ideal II § no.
Graded tensor product of type 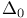 III § no. III § no.
Graduation compatible with a coproduct III § no.
Graduation compatible with an algebra structure III § no.
Graduation induced, quotient graduation II § no.
Graduation of type A II § no.
Graduation, partial, total graduation II § nos.
Graduation, trivial II § no.
Grassmann relations III § no.
Grassmannian III §11 no.
Greatest common divisor (g.c.d.) of two integers I §8 no.
Group I § no.
Group commutator I § no.
Group defined by generators and relations I § no.
Group of differences, group of fractions I § no.
Group of exponential type I § Exercise
Group operating faithfully I § no.
Group operating freely I § no.
Group operating simply transitively I § no.
Group operating transitively I § no.
Group with operators I § no.
Group with operators, Abelian, commutative I § no.
Group with operators, product I § no.
Group with operators, product (or internal product), of a family of quotient groups I § no.
Group with operators, quotient I § no.
Group with operators, simple I § no.
Group, additive, of a ring I § no.
Group, affine I § no.
Group, alternating I § no.
Group, bicyclic I § Exercise
Group, bigraded II § no.
Group, concidence, of two homomorphisms I § no.
Group, cyclic I §4 no.
Group, derived I § no.
Group, dihedral I § Exercise
Group, finite, infinite group I § no.
Group, finitely generated I § Exercise
Group, finitely presented I § Exercise
Group, free commutative, over a set I § no. § no.
Group, free, over a set I § no.
Group, graded II § no.
Group, linear II § no.
Group, minimal simple I § Exercise
Group, monogenous I § no.
Group, multiplicative, of a ring I § no.
Group, nilpotent, nilpotent group of class n I § no.
Group, projective II § no.
Group, residually finite I § Exercise
Group, solvable, solvable group of class n I § no.
Group, special linear III § no.
Group, supersolvable I § Exercise
Group, symmetric I § no.
Group, unimodular III § no.
Groupoid I § Exercise
Hall's theorem I § Exercise
Hamel basis II § no.
Hamiltonian quaternions III § no.
Homogeneous element in a graded group II § no.
Homogeneous G-set I § no.
Homogeneous linear equation, linear system II § no.
Homogeneous subset of degree p in a formal power series III § no.
Homogeneous subset of degree p with respect to certain indeterminates in a formal power series III § no.
Homomorphism for two laws of composition I § no.
Homomorphism of groups with operators I § no.
Homomorphism, A-module, A-homomorphism II § no.
Homomorphism, algebra III § no.
Homomorphism, central ring II § no.
Homomorphism, crossed I § Exercise
Homomorphism, essential II § Exercise
Homomorphism, graded II § no.
Homomorphism, graded algebra III § no.
Homomorphism, group I § no.
Homomorphism, M-set I § no.
Homomorphism, monoid I § no.
Homomorphism, multimodule II § no.
Homomorphism, projection I §4 no.
Homomorphism, ring I § no.
Homomorphism, trivial I § no.
Homomorphism, unital I § no.
Homomorphism, unital algebra III § no.
Homothety I § no. § no.
Homothety, central II § no. § Exercise
Hyperplane at infinity II § no.
Hyperplane passing through 0 in a vector space II § no.
Hyperplane, affine II §9 no.
Hyperplane, projective II § no.
Hyperplane, projective, taken as hyperplane at infinity II § no.
Ideal of relators III § no.
Ideal, discriminant III §9 no.
Ideal, graded II § no. § no.
Ideal, irreducible two-sided I § Exercise
Ideal, left, right ideal, two-sided ideal in a ring I § no.
Ideal, left, right ideal, two-sided ideal in an algebra III § no.
Ideal, maximal I § no.
Ideal, prime I § no.
Ideal, principal I § no.
Ideal, zero I § no.
Idempotent I § no.
Identities, Jacobi, between minors of a determinant III § Exercise
Identities, polynomials III § no.
Identity element I § no.
Identity, Jacobi III § no 6
Identity, Redei III § Exercise
Image (inverse image) of a projective linear variety under a projective mapping II § no.
Image of a homomorphism II § no.
Indeterminate, indeterminate of index a I § no. § no.
Index of a subgroup I § no.
Induced 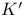 -structure II § no. -structure II § no.
Induced action I § no.
Induced graduation II § no.
Induced law I § no.
Infinity, hyperplane at II § no.
Infinity, points at II § no.
Inner automorphism of a group I § no.
Inner automorphism of a ring I § no.
Inner product, left, right III § nos.
Integer, negative, positive, strictly negative, strictly positive I § no.
Integer, rational I § no.
Integers, rational, modulo a (ring of) I § no.
Integers, relatively prime I § no.
Integral domain I § no.
Integrity, domain of I § no.
Internal direct product, restricted sum I § no.
Invariant element I § no.
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



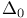
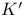 -structure
-structure