|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| McConnell J.C., Robson J.C. — Noncommutative Noetherian Rings |
|
|
 |
| Предметный указатель |
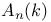 , , 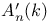 see “Weyl algebra” see “Weyl algebra”
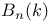 see “Weyl algebra” see “Weyl algebra”
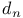 6.6.18 (see also “Weyl algebra”) 6.6.18 (see also “Weyl algebra”)
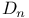 , polynomials over 9.6.12 , polynomials over 9.6.12
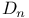 , subfields of 6.6.18 , subfields of 6.6.18
 -group see “Grothendieck group” -group see “Grothendieck group”
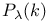 , , 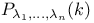 1.8.7 1.8.7
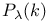 , , 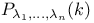 , being Dedekind domain 5.2.11 7.11.3 , being Dedekind domain 5.2.11 7.11.3
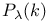 , , 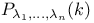 , being simple Noetherian 1.8.7 , being simple Noetherian 1.8.7
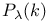 , , 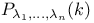 , global dimension of 7.5.4 , global dimension of 7.5.4
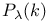 , , 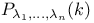 , global dimension of overrings of 9.1.13 , global dimension of overrings of 9.1.13
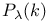 , , 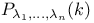 , Krull dimension of 6.5.4 6.6.12 , Krull dimension of 6.5.4 6.6.12
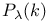 , , 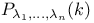 , Krull dimension of overrings of 9.1.13 , Krull dimension of overrings of 9.1.13
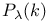 , , 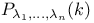 , matrices over 7.11.7 , matrices over 7.11.7
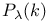 , , 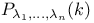 , skew group ring over 7.8.14 12.7.16 , skew group ring over 7.8.14 12.7.16
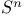 see “Coordinate ring” see “Coordinate ring”
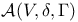 14.8.1 ff 14.8.1 ff
a.c.c 0.1.2
Additive function 12.1.7
Additive reduced rank being 4.1.2
Additivity 4.5.1 ff
Additivity, principle 4.5.9 14.0.0
Adjoint representation 14.1.2
Ado and Iwasawa’s Theorem 1.7.1
Affiliated chain 4.4.6
Affiliated prime 4.3.4
Affiliated sequence 4.4.6
Affine algebra 8.1.9
Affine PI algebra 13.10.1 ff
Algebra, affine 8.1.9
Algebra, almost commutative 8.4.2
Algebraic Lie algebra 14.7.2
Almost centralizing, derivation ring being 15.1.20
Almost centralizing, extension 8.6.6
Almost commutative algebra 8.4.2
Almost commutative algebra, not 14.3.9
Almost normalizing extension 1.6.10
Almost normalizing extension, generic flatness of 9.4.11
Almost normalizing extension, Noetherian 1.6.14
Amitsur — Levitzki theorem 13.3.3
Annihilator 2.1.10
Annihilator, ideal 2.2.15
Annihilator, maximal 2.3.2
Antichain 6.1.1
AR ring 4.2.3
Arithmetic of ideals 5.2.9
Artin radical 4.1.7
Artin — Procesi theorem 13.7.14 13.11.7
Artin — Rees property 4.1.10 4.2.3
Artin — Rees property, and localization 4.2.9 ff 6.8.21
Artin — Tate lemma 13.9.10
Artin — Wedderburn theory 0.1.9
Artinian quotient ring, additivity and 4.5.9
Artinian quotient ring, affiliated primes and 4.4.10
Artinian quotient ring, and largest stable ideal 6.9.10
Artinian quotient ring, existence of 4.1.4
Artinian quotient ring, FBN and 6.8.16
Artinian quotient ring, hereditary ring has 5.4.2
Artinian quotient ring, ideal invariance and 6.8.15
Artinian quotient ring, Krull dimension and 6.8.1 ff
Artinian, module 0.1.2
Artinian, ring 0.1.6
Asano prime ring 5.2.7
Asano prime ring, PI 13.9.15
Associated graded ring (of filtered ring) 1.6.1 ff
Associated graded ring (of filtered ring),  of 12.1.10 12.3.5 12.6.1 of 12.1.10 12.3.5 12.6.1
Associated graded ring (of filtered ring), being generically flat 9.4.9
Associated graded ring (of filtered ring), being integral domain 1.6.6
Associated graded ring (of filtered ring), being Noetherian 1.6.9
Associated graded ring (of filtered ring), being non-Noetherian 8.3.9
Associated graded ring (of filtered ring), being prime 1.6.6
Associated graded ring (of filtered ring), GK dimension of 8.1.14 8.3.20 8.6.1 8.7.6
Associated graded ring (of filtered ring), global dimension of 7.6.18
Associated graded ring (of filtered ring), Krull dimension of 6.5.6
Associated graded ring (of filtered ring), module theory of 7.6.1 ff
Associated graded ring (of filtered ring), of derivation ring 15.4.5 ff
Associated graded ring (of filtered ring), of enveloping algebra 1.7.5
Associated graded ring (of filtered ring), of filtered ring 1.6.4
Associated prime 4.3.9 4.4.2 4.4.4
Augmentation ideal of enveloping algebra 14.3.8
Augmentation ideal of graded ring 12.2.3
Augmentation ideal of symmetric algebra 15.1.18
Augmentation map 14.3.8
Automorphism, inner 1.8.2
Automorphism, outer 7.8.12
Automorphism, X-inner 10.3.10 10.6.15
Azumaya 13.7.6 13.7.13
Azumaya algebra 13.7.6 13.7.13
Azumaya,  -symmetric 14.8.3 -symmetric 14.8.3
Azumaya, central separable 13.7.8
Azumaya, central simple 5.3.4
Azumaya, constructible 9.4.12
Azumaya, exterior 13.4.5
Azumaya, filtered 9.4.9
Azumaya, of group 10.3.13 10.4.6
Azumaya, somewhat commutative 8.6.9
Azumaya, symmetric 15.1.18
Basic, composition series 11.6.2
Basic, dimension 11.6.2 11.8.6
Basic, element 11.8.7
Bass’ theorem 11.7.4 11.7.13
Bernstein number 8.4.7
Bimodule, condition 4.5.7
Bimodule, prime 4.3.4
Bimodule, question 6.4.11
Bound 10.1.7
Bounded 6.4.7
Bounded, fully 6.4.7
Bracket product 1.7.1
Brandt groupoid 5.2.14
c-integral 5.3.2
Cancellation of modules 11.4.1 ff 11.7.1 11.8.7
Cancellation, rank 11.5.20
Capelli polynomial 13.5.5
Category, admissible 12.4.2
Category, equivalence 3.5.7 3.7.5
Category, Grothendieck group of 12.4.3
Catenary property 13.10.13
Catenary property in U(g) 14.10.2
Central extension 13.1.11
Central polynomial 13.5.2 13.6.1
Central separable algebra 13.7.8
Central simple algebra 5.3.4 13.3.1
Central simple algebra, having central polynomial 13.6.3
centralizer 3.2.6 10.3.8
Centralizing sequence 4.1.13
Centralizing sequence, in enveloping algebra 14.3.4
Characteristic, closure 13.9.2
Characteristic, ideal 8.7.6
Class group, ideal 12.1.6
Class group, projective 12.1.5
Classical order 5.3.5
Classical order, having central polynomial 13.6.3
CLIQUE 4.3.7
Closed centrally 10.3.13
Closed G 10.3.13
Closed normally 10.3.13
Closure, central 10.3.13
Closure, G 10.3.13
Closure, normal 10.3.13
Codeviation 6.1.8
Common multiple property 2.2.5
Complement 2.2.3
Completely faithful module 5.7.3
Completely faithful module and stable range 6.7.7
Completely integrally closed 5.1.3
Completely integrally closed, characterization of 5.3.3
Completely prime ideal 0.2.2
Completely prime ideal in enveloping algebra 14.2.11
Completely solvable 7.5.7 14.1.8
| Compressible 6.9.3
Constructive algebra 9.4.12
Constructive algebra, derivation ring being 15.1.22
Context, equivalent 3.6.4
Context, Morita 1.1.6
Context, prime 3.6.5
Coordinate ring of 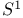 , ,  of 12.1.6 of 12.1.6
Coordinate ring of 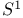 , ,  of derivation ring of 15.4.8 of derivation ring of 15.4.8
Coordinate ring of 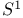 , derivations of 15.3.13 , derivations of 15.3.13
Coordinate ring of 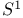 , is Dedekind domain 7.8.14 , is Dedekind domain 7.8.14
Coordinate ring of 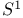 , overling of 12.7.8 , overling of 12.7.8
Coordinate ring of 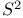 , Der - is not free 15.3.15 , Der - is not free 15.3.15
Coordinate ring of 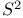 , has stably free module 11.2.3 , has stably free module 11.2.3
Coordinate ring of 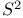 , ranks of 11.5.4 , ranks of 11.5.4
Coordinate ring of algebraic variety 15.0.0
Coordinate ring of cusp 15.3.12 15.4.10
Critical 6.2.9
Critical, composition series 6.2.19
Critical, for dimension function 6.8.25
Critical, ideal 6.3.4
Crossed product 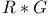 see “Group ring” see “Group ring”
Crossed product, 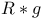 1.9.9 1.9.9
Crossed product, 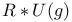 see “Enveloping algebra” see “Enveloping algebra”
Cusp see “Coordinate ring”
Cutting down 10.2.4
Cutting down in enveloping algebra 14.2.5 14.5.4
Cutting down in fixed ring 10.5.15
Cutting down in group ring 10.5.6
d.c.c 0.1.2
Dedekind domain/prime ring 5.2.10
Dedekind domain/prime ring, 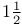 generators in 5.7.12 generators in 5.7.12
Dedekind domain/prime ring, commutative 5.2.8 5.7.18
Dedekind domain/prime ring, module theory of 5.7.1 ff 7.11.4 11.7.14 11.8.7
Dedekind domain/prime ring, PI 13.9.14
Dedekind domain/prime ring, simple 7.11.1 ff
Degree of function 8.1.7
Degree of ordinal 6.1.9
Degree of polynomial 1.2.8 9.6.6
Degree of polynomial element 6.9.17
Degree of polynomial identity 13.1.2
Degree, in filtered module 7.6.7
Degree, minimal 13.2.2
Degree, PI 13.3.6 13.6.7
Degree, total 9.4.15
Degree, transcendence 8.2.14 13.10.5
Denominator set 2.1.13
Dense, right ideal 10.3.4
Dense, subring 0.3.5
Density theorem 0.3.6
Derivation ring 15.1.4 ff
Derivation ring, associated graded ring of 15.4.5 ff
Derivation(s) and localization 14.2.2
Derivation(s) and prime ideals 14.2.3
Derivation(s), 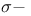 1.2.1 1.2.1
Derivation(s), inner 1.8.2
Derivation(s), k- 1.7.10 15.1.2
Derivation(s), k-, to module 15.1.7
Derivation(s), locally nilpotent 14.6.4
Derivation(s), universal 15.1.8
Derivation(s), universal bimodule of 8.7.3
Deviation 6.1.2
Differential operator(s) see also “Derivation ring”
Differential operator(s), asymmetry of 15.6.5
Differential operator(s), order of 15.4.11 15.5.2
Differential operator(s), ring of 15.0.0 ff 15.5.1 15.6.5
Differentials (Kahler) 15.1.8 15.6.1
Differentials (Kahler) of regular ring 15.2.12
Dimension, basic 11.6.2 11.8.6
Dimension, classical Krull 6.4.4
Dimension, exact function 6.8.4
Dimension, flat 7.1.4
Dimension, function 6.8.4
Dimension, Gabriel 6.10.0
Dimension, Gelfand — Kirillov 8.1.11 8.1.16
Dimension, GK 8.1.11 8.1.16
Dimension, global 7.1.8
Dimension, Goldie 2.2.10
Dimension, injective 7.1.3
Dimension, Kronecker 11.5.9
Dimension, Krull 6.2.2
Dimension, projective 7.1.2
Dimension, uniform 2.2.10
Dimension, weak 7.1.4
Dimension, weak global 7.1.9
Discriminant 13.8.11
Dual basis lemma 3.5.2
Dual module 3.4.4
Eigen, ring 1.1.11
Eigen, value 14.1.16
Eigen, vector 14.1.15
Eisenbud — Evans theorem 11.7.4
Element, automorphic 10.1.3
Element, c-integral 5.3.2
Element, centralizes 10.1.3
Element, homogeneous 1.6.3 7.6.3 10.6.7
Element, integral 5.3.2
Element, minimal 9.4.18
Element, nilpotent 0.2.5
Element, normal 4.1.10
Element, normalizes 10.1.3
Element, regular 2.1.2
Element, strongly nilpotent 0.2.5
Elementary group 11.3.5
Elementary range 11.3.9
Elementary rank 11.3.10
Endomorphism property over k 9.1.4
Endomorphism property, over K 9.2.3
Endomorphism ring, algebraic 9.1.4 ff
Endomorphism ring, and matrices 8.2.8
Endomorphism ring, finite dimensional 9.5.1 ff
Endomorphism ring, of uniform ideal 3.3.5
Endomorphism ring, over PI ring 13.4.9
Endomorphism ring, over semiprime ring 3.4.1 ff
Enveloping algebra (skew, crossed product) 1.7.1 ff 14.0.0
Enveloping algebra (skew, crossed product),  of 12.6.14 of 12.6.14
Enveloping algebra (skew, crossed product), associated graded ring of 1.7.5
Enveloping algebra (skew, crossed product), being .almost commutative 8.4.1 ff
Enveloping algebra (skew, crossed product), being almost centralizing 8.6.6
Enveloping algebra (skew, crossed product), being almost normalizing 1.7.14
Enveloping algebra (skew, crossed product), being constructible 9.4.12
Enveloping algebra (skew, crossed product), being integral domain 1.7.5 1.7.14
Enveloping algebra (skew, crossed product), being maximal order 5.1.6
Enveloping algebra (skew, crossed product), being Noetherian 1.7.4 1.7.14
Enveloping algebra (skew, crossed product), being prime 1.7.14
Enveloping algebra (skew, crossed product), being regular 7.7.5
Enveloping algebra (skew, crossed product), being somewhat commutative 8.6.10
Enveloping algebra (skew, crossed product), crossed product 1.7.12
Enveloping algebra (skew, crossed product), crossed product construction 1.9.7 1.9.9
Enveloping algebra (skew, crossed product), example of 15.3.14
Enveloping algebra (skew, crossed product), GK dimension of 8.1.15 8.2.10
Enveloping algebra (skew, crossed product), global dimension of 7.5.7 7.6.10
Enveloping algebra (skew, crossed product), having finite endomorphism ring 9.5.5
Enveloping algebra (skew, crossed product), having projectives stably free 12.3.3
Enveloping algebra (skew, crossed product), Krull dimension of 6.5.7 6.6.2
Enveloping algebra (skew, crossed product), not simple 1.7.5
Enveloping algebra (skew, crossed product), Nullstellensatz for overrings of 9.4.22
Enveloping algebra (skew, crossed product), Nullstellensatz in 9.1.8 14.4.1
Enveloping algebra (skew, crossed product), of sl(2, k) 8.5.12
Enveloping algebra (skew, crossed product), of solvable Lie algebra 14.1.1 ff
Enveloping algebra (skew, crossed product), Poincare — Birkhoff — Witt theorem for 1.7.5 1.9.7 1.9.9
Enveloping algebra (skew, crossed product), prime ideals in 14.2.1 ff 14.3.1
Enveloping algebra (skew, crossed product), primitive ideals in 14.4.1 ff
Enveloping algebra (skew, crossed product), second layer condition in 4.3.14
Enveloping algebra (skew, crossed product), semicentre of 14.4.6
Enveloping algebra (skew, crossed product), simple 1.8.3
Enveloping algebra (skew, crossed product), skew 1.7.10
Enveloping algebra (skew, crossed product), smash product 1.9.7
Enveloping algebra (skew, crossed product), stably free ideals of 11.2.14
Enveloping algebra (skew, crossed product), standard monomials in 1.7.5
Enveloping algebra (skew, crossed product), universal property of 1.7.2
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



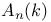 ,
, 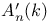
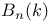
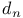
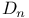 , polynomials over
, polynomials over  -group
-group 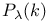 ,
, 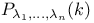
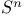
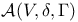
 -symmetric
-symmetric 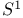 ,
, 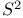 , Der - is not free
, Der - is not free 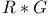
 generators in
generators in