|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| McConnell J.C., Robson J.C. — Noncommutative Noetherian Rings |
|
|
 |
| Предметный указатель |
Equivalent, orders 3.1.9
Equivalent, right orders 5.6.5
Essential right ideal 2.2.1
Essential right ideal, contains regular element 2.3.5
Essential right ideal, has regular generators 3.3.7
Essential submodule 2.2.1
Essentiality 10.2.11
Evaluation 13.5.2
Exponential growth 8.1.8
Ext 7.1.12
Extension 1.6.2
Extension, almost centralizing 8.6.6
Extension, almost normalizing 1.6.10
Extension, automorphic 10.1.3
Extension, c-integral 5.3.2
Extension, central 13.1.11
Extension, centralizing 10.1.3
Extension, essential 2.2.1
Extension, finite 10.1.2
Extension, integral 5.3.2 10.7.0 13.8.1
Extension, normalizing 10.1.3
Extension, Ore 1.9.2
Faith — Utumi theorem 3.2.6
Faithful module 0.3.2
Faithful module, completely 5.7.3
FBN 6.4.7
FBN, Artinian quotient ring of 6.8.16 ff
FBN, characterization of 6.10.4
FBN, Jacobson conjecture for 6.4.15
FBN, PI ring 13.6.6
FBN, second layer condition for 4.3.14
Filtered homomorphism 7.6.8
Filtered K-algebra 9.4.9
Filtered module 7.6.8
Filtered ring see “Associated graded ring”
Filtration(s), equivalent 8.6.12
Filtration(s), finite dimensional 8.1.9
Filtration(s), good 8.6.3
Filtration(s), having bounded difference 8.6.12
Filtration(s), of derivation ring 15.1.19
Filtration(s), of module 7.6.7
Filtration(s), of ring 1.6.1
Filtration(s), standard 1.6.2 7.6.7 8.1.9
Filtration(s), translate of 8.6.14
Fitting’s Lemma 2.3.2
Fixed ring 7.8.1 ff 10.5.1
Flat, (n, m)-generically 9.3.12 9.3.16
Flat, dimension 7.1.4
Flat, faithfully 7.2.3 15.2.13
Flat, generically 9.3.2
Flat, module 7.1.4
Flat, resolution 7.1.4
Forster — Swan theorem 11.7.4
Fractional ideal 3.1.11
Fractional ideal, order of 3.1.12
Fractional ideal, reflexive 5.1.8
Free filtered 7.6.15
Free graded 7.6.5
G-domain 9.3.9
G-ideal 9.3.9
G-ring 13.9.12 14.5.6
Gabriel dimension 6.10.0
Gabriel H-condition 6.10.4
Gelfand — Kirillov dimension 8.0.0 ff 8.1.11 8.1.16
Gelfand — Kirillov dimension and transcendence degree 8.2.14
Gelfand — Kirillov dimension of  15.4.7 15.4.7
Gelfand — Kirillov dimension of  14.8.13 14.8.13
Gelfand — Kirillov dimension of derivation ring 14.3.2 14.3.6
Gelfand — Kirillov dimension of modules over 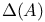 15.4.1 ff 15.4.1 ff
Gelfand — Kirillov dimension of PI ring 13.10.6
General linear group 11.1.11
General linear range 11.1.12
General linear rank 11.1.14
Generating subspace for module 8.1.9
Generating subspace for ring 8.1.9
Generative 5.5.3
Generator 3.5.3
Generic flatness 9.3.1 ff
Generic regularity 4.6.11
GK dimension see “Gelfand — Kirillov dimension”
Global dimension 7.0.0 ff 7.1.8
Global dimension of  15.4.7 15.4.7
Global dimension of  14.8.13 14.8.13
Global dimension of commutative rings 7.1.15 15.2.8
Global dimension of derivation ring 15.3.2 15.3.7
Global dimension, weak 7.1.9
Going down in fixed ring 10.5.15
Going down in group ring 10.5.12
Going down in PI ring 13.8.13
Going up in fixed ring 10.5.15
Going up in normalizing extension 10.2.10
Going up in PI ring 13.8.14
Goldie, dimension 2.2.10
Goldie, normalizing extension being 10.1.11
Goldie, rank 14.0.0
Goldie, rank polynomial 14.0.0
Goldie, ring 2.3.1
Goldie, Theorem 2.3.6
Goldie, Theorem\l 3.1.7
Graded division ring 10.3.19
Graded homomorphism 7.6.3 12.2.3
Graded ring 1.6.3 (see also “Associated graded ring”)
Graded ring element, degree of 1.6.4
Graded ring element, homogeneous 1.6.3 10.3.19
Graded ring element, homogeneous component of 1.6.7
Graded ring element, leading term of 1.6.4
Graded ring,  of 12.1.10 of 12.1.10
Graded ring,  12.4.10 12.4.10
Graded ring, graded right ideal of 1.6.7
Graded ring, group 10.3.18
Graded simple 10.3.19
Grading 7.6.2
Grading, product 12.2.5
Grading, translate of 7.6.2
Grading, trivial 12.2.2
Grothendieck group ( ) 12.0.0 ff ) 12.0.0 ff
Grothendieck group ( ) of category 12.4.3 ) of category 12.4.3
Grothendieck group ( ) of derivation ring 15.4.8 ) of derivation ring 15.4.8
Grothendieck group ( ) of filtered ring 12.3.5 12.6.13 ) of filtered ring 12.3.5 12.6.13
Grothendieck group ( ) of graded ring 12.1.10 ) of graded ring 12.1.10
Grothendieck group ( ) of ring 12.1.2 ) of ring 12.1.2
Group ring (skew, crossed product) 1.5.1 ff
Group ring (skew, crossed product),  of 12.5.1 ff 12.7.1 of 12.5.1 ff 12.7.1
Group ring (skew, crossed product), being constructive 9.4.12
Group ring (skew, crossed product), being Noetherian 1.5.11 1.5.12
Group ring (skew, crossed product), being normalizing extension 10.1.4
Group ring (skew, crossed product), being regular 7.7.5
Group ring (skew, crossed product), being simple 1.8.3 7.8.12
Group ring (skew, crossed product), crossed product 1.5.8
Group ring (skew, crossed product), fixed ring of 7.8.1 ff 10.5.1
Group ring (skew, crossed product), GK dimension of 8.2.9 8.2.18
Group ring (skew, crossed product), global dimension of 7.5.6 7.8.1
Group ring (skew, crossed product), having finite endomorphism ring 9.5.5
Group ring (skew, crossed product), having projectives stably free 12.3.3
Group ring (skew, crossed product), Krull dimension of 6.5.5 6.6.1
Group ring (skew, crossed product), Nullstellensatz for 9.1.8 9.4.22
Group ring (skew, crossed product), poly cyclic by finite 1.5.12
Group ring (skew, crossed product), prime ideals in 10.5.1 ff
Group ring (skew, crossed product), second layer condition in 4.3.14
Group ring (skew, crossed product), skew 1.5.4
Group ring (skew, crossed product), stably free ideals of 11.2.8
Group ring (skew, crossed product), twisted 1.5.8
Group ring (skew, crossed product), universal property of 1.5.2 1.5.6
Heisenberg group 1.5.3 1.5.10 8.2.17
Heisenberg Lie algebra 1.7.7
Hereditary ring(s) 5.2.2
Hereditary ring(s), and idealizers 5.6.1 ff
Hereditary ring(s), and idempotents 7.8.9
Hereditary ring(s), being simple 7.11.1 ff
Hereditary ring(s), examples of 7.8.14
| Hereditary ring(s), fixed ring of 7.8.8
Hereditary ring(s), Krull dimension of 6.2.8
Hereditary ring(s), prime PI 13.9.16
Hereditary ring(s), structure of 5.4.1 ff
Hilbert polynomial 8.4.6
Hilbert polynomial in somewhat commutative algebra 8.6.19
Hirsch number 6.5.5
Holonomic module 8.5.8
Holonomic module over derivation ring 15.6.4
Homogeneous, component 1.6.7 7.6.3
Homogeneous, element 1.6.3 7.6.3 10.6.7
Homogeneous, module w.r.t. dimension function 6.8.8
Homomorphism, filtered 7.6.7
Homomorphism, graded of modules 7.6.3
Homomorphism, graded of rings 12.2.3
Homomorphism, strict filtered 7.6.12
Hopkins’ theorem 0.1.13
Ideal invariance 6.4.16 6.8.13
Ideal invariance, and GK dimension 8.3.16
Ideal(s) (right, left), annihilator 2.1.10 2.2.15
Ideal(s) (right, left), augmentation 12.2.3 14.3.8 15.1.18
Ideal(s) (right, left), characteristic 8.7.6
Ideal(s) (right, left), class group 12.1.6
Ideal(s) (right, left), completely prime 0.2.2
Ideal(s) (right, left), critical 6.3.4
Ideal(s) (right, left), dense 10.3.4
Ideal(s) (right, left), essential 2.2.1
Ideal(s) (right, left), fractional 3.1.11
Ideal(s) (right, left), G-stable 10.5.4
Ideal(s) (right, left), generative 5.5.3
Ideal(s) (right, left), graded 1.6.7 10.3.19
Ideal(s) (right, left), integral 3.1.13
Ideal(s) (right, left), invariant 6.8.13
Ideal(s) (right, left), invertible 4.2.5 5.2.5
Ideal(s) (right, left), isomaximal 5.5.2
Ideal(s) (right, left), localizable 4.0.0
Ideal(s) (right, left), nilpotent 0.1.11
Ideal(s) (right, left), prime 0.2.3
Ideal(s) (right, left), primitive 0.3.4
Ideal(s) (right, left), semimaximal 5.8.5
Ideal(s) (right, left), semiprime 0.2.7
Ideal(s) (right, left), semiprimitive 0.3.9
Ideal(s) (right, left), stable 1.8.2
Ideal(s) (right, left), subisomorphic 3.3.4
Ideal(s) (right, left), T 13.1.4
Ideal(s) (right, left), trace 10.5.16
Idealizer ring 1.1.11 5.5.1
Idealizer ring, and differential operators 15.5.13
Idealizer ring, chain conditions of 1.1.12
Idealizer ring, example (in Weyl algebra) of 1.3.10
Idealizer ring, global dimension of 7.5.11 ff
Idealizer ring, Krull dimension of 6.5.2
Idealizer ring, multiple 5.8.5
Identity, algebra polynomial 13.1.15
Identity, alternating 13.1.12
Identity, monic 13.1.2
Identity, multilinear 13.1.8
Identity, polynomial 13.1.2
Identity, stable 13.1.16
Identity, standard 13.1.3
Incoihparability 10.2.13 10.4.1
Incoihparability in enveloping algebra 14.2.8
Incoihparability in PI ring 13.8.14
Incoihparability in skew polynomial ring 10.6.6 14.2.9
Incoihparability, theorem 10.4.15
Index of nilpotency 3.2.7
Injective, dimension 7.1.3
Injective, envelope 4.3.2
Injective, resolution 7.1.3
Integral, c- 5.3.2
Integral, domain 0.2.2
Integral, element 5.3.2
Integral, extension 10.7.0 13.8.1
Integral, ideal 3.1.13
Integrally closed 5.3.3
Integrally closed, completely 5.1.3
Intersection condition 4.3.17
Invariant(s), basis property 11.1.2
Invariant(s), ideal 6.8.13
Invariant(s), ideal, ring 6.8.13
Invariant(s), in enveloping algebra 14.1.15
Invariant(s), ring of see “Fixed ring”
Invariant(s), weakly, ideal 6.8.13
Invertible ideal 4.2.5 5.2.5
Irreducible module 0.1.2
Irreducible ring 6.8.17
Isomaximal 5.5.2
Isotypic 0.1.2
Jacobi identity 1.7.1
Jacobson conjecture 6.10.4
Jacobson conjecture, example of 4.3.20 4.7.3
Jacobson conjecture, for FBN rings 6.4.15
Jacobson, derivation ring being 15.1.22
Jacobson, PI ring 13.10.3
Jacobson, radical 0.3.8
Jacobson, ring 9.1.2 ff 9.7.1
Jordan — Holder, theorem 0.1.3
Jordan — Holder, weights 14.4.10
Kaplansky’s Theorem 13.3.8
Koszul resolution and global dimension 7.3.16
Koszul resolution and Krull dimension 6.5.9
Kothe conjecture 0.2.9
Kothe conjecture for PI rings 13.2.5
Krull dimension 6.0.0 ff
Krull dimension, and GK dimension 8.3.18
Krull dimension, and monic localization 7.9.4
Krull dimension, classical 6.4.4
Krull dimension, of  15.4.7 15.4.7
Krull dimension, of  14.8.13 14.8.13
Krull dimension, of derivation ring 15.3.7
Krull dimension, of enveloping algebra 14.7.6
Krull dimension, of fixed rings 7.8.8
Krull dimension, of module 6.2.2
Krull dimension, of normalizing extension 10.1.10
Krull dimension, of ring 6.2.2 6.3.1
Krull dimension, of simple rings 7.11.1 ff
Krull dimension, of U(sl(2, k)) 8.5.12 ff
Krull dimension, symmetry of 6.4.10 14.10.8
Krull socle 6.2.14
Krull, domain 5.1.10
Krull, ring 5.8.1
Kurosch problem 13.8.9
Leading coefficient of polynomial 1.2.8 7.9.5 9.6.6
Leading right ideal 1.2.9 1.8.5 9.4.16
Length in skew Laurent polynomial ring 6.9.14 10.6.7
Length of chain Notation
Lie algebra(s) 1.7.1
Lie algebra(s), abelian 14.1.5
Lie algebra(s), acting locally nilpotently 14.1.13
Lie algebra(s), acting nilpotently 14.1.13
Lie algebra(s), acting semisimply 14.1.12
Lie algebra(s), adjoint representation of 14.1.2
Lie algebra(s), algebraic 14.7.2
Lie algebra(s), completely solvable 7.5.7 14.1.8
Lie algebra(s), eigenvalue of 14.1.16
Lie algebra(s), eigenvector of 14.1.15
Lie algebra(s), Heisenberg 1.7.7
Lie algebra(s), ideal of 14.1.2
Lie algebra(s), invariant of 14.1.16
Lie algebra(s), module over 14.1.3
Lie algebra(s), nilpotent 14.1.6
Lie algebra(s), over ring 1.7.8
Lie algebra(s), representation of 1.7.1
Lie algebra(s), semi-invariant of 14.1.15
Lie algebra(s), semidirect product of 1.7.11
Lie algebra(s), semisimple 14.1.12
Lie algebra(s), solvable 6.6.2 14.1.7
Lie algebra(s), triangular module over 14.1.3
Lie algebra(s), universal enveloping algebra of 1.7.2
Lie product 1.7.1
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте





 of
of 