|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rencher A.C., Barnett V., Bradley R.A. (Ed) Ч Multivariate Statistical Inference and Applications |
|
|
 |
| ѕредметный указатель |
 -tests 60Ч120 -tests 60Ч120
 -tests and discriminant function 74 92 109 -tests and discriminant function 74 92 109
 -tests and F-distribution 67 -tests and F-distribution 67
 -tests and multivariate quality control 114Ч115 -tests and multivariate quality control 114Ч115
 -tests and quality control 114Ч115 -tests and quality control 114Ч115
 -tests for elliptically contoured distributions 112Ч113 -tests for elliptically contoured distributions 112Ч113
 -tests on a sub vector 108Ч112 -tests on a sub vector 108Ч112
 -tests on a sub vector, covariates 110 -tests on a sub vector, covariates 110
 -tests, additional information, test for 108Ч112 -tests, additional information, test for 108Ч112
 -tests, approximate tests, nonparametric tests 113 -tests, approximate tests, nonparametric tests 113
 -tests, approximate tests, when -tests, approximate tests, when 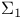 , , 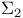 99Ч104 99Ч104
 -tests, Behrens Ч Fisher problem 99Ч104 -tests, Behrens Ч Fisher problem 99Ч104
 -tests, Behrens Ч Fisher problem, multivariate 100Ч104 -tests, Behrens Ч Fisher problem, multivariate 100Ч104
 -tests, Behrens Ч Fisher problem, univariate 99Ч100 -tests, Behrens Ч Fisher problem, univariate 99Ч100
 -tests, degrees of freedom 65 -tests, degrees of freedom 65
 -tests, effect of each variable 67Ч70 87Ч91 -tests, effect of each variable 67Ч70 87Ч91
 -tests, formal definition of -tests, formal definition of  66 66
 -tests, likelihood ratio test 71Ч72 91Ч92 -tests, likelihood ratio test 71Ч72 91Ч92
 -tests, matched pairs 97Ч99 -tests, matched pairs 97Ч99
 -tests, one mean vector, -tests, one mean vector,  known 60Ч61 known 60Ч61
 -tests, one mean vector, -tests, one mean vector,  unknown 65Ч74 unknown 65Ч74
 -tests, paired observation test 97Ч99 -tests, paired observation test 97Ч99
 -tests, power 104Ч108 -tests, power 104Ч108
 -tests, power, tables 106 423Ч426 -tests, power, tables 106 423Ч426
 -tests, properties of 70 91 -tests, properties of 70 91
 -tests, robust versions of -tests, robust versions of  -ests 114 -ests 114
 -tests, robustness of -tests, robustness of  -tests to nonnormality 96Ч97 -tests to nonnormality 96Ч97
 -tests, robustness of -tests, robustness of  -tests to unequal covariance matrices 96 -tests to unequal covariance matrices 96
 -tests, selection of variables 111 -tests, selection of variables 111
 -tests, stepdown test 110Ч111 -tests, stepdown test 110Ч111
 -tests, table of critical values 419Ч420 -tests, table of critical values 419Ч420
 -tests, transformation to F 67 -tests, transformation to F 67
 -tests, two mean vectors, -tests, two mean vectors, 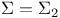 85Ч92 85Ч92
 -tests, two mean vectors, -tests, two mean vectors,  100Ч104 100Ч104
 -tests, union-intersection test 72Ч74 92 -tests, union-intersection test 72Ч74 92
Additional information, test on see УTests of hypotheses on
Analysis of covariance 110 178Ч194
Analysis of covariance, multivariate 187Ч194
Analysis of covariance, multivariate and canonical correlations 190
Analysis of covariance, multivariate, one-way model 187
Analysis of covariance, multivariate, two-way model 188
Analysis of covariance, univariate 178Ч187
Analysis of covariance, univariate, assumptions 178Ч179
Analysis of covariance, univariate, one-way model 179Ч183
Analysis of covariance, univariate, two-way model 183Ч186 191
Analysis of covariance, univariate, unbalanced model 186Ч187
Analysis of variance, multivariate see УMultivariate analysis of varianceФ
Analysis of variance, univariate (ANOVA), contrasts 142Ч145
Analysis of variance, univariate (ANOVA), contrasts, Bonferroni procedure 144
Analysis of variance, univariate (ANOVA), contrasts, orthogonal 144
Analysis of variance, univariate (ANOVA), contrasts, Scheffe procedure 144Ч145
Analysis of variance, univariate (ANOVA), unbalanced data 152Ч155 160Ч168
Analysis of variance, univariate (ANOVA), unbalanced data, cell means model 152 160Ч161
Analysis of variance, univariate (ANOVA), unbalanced data, contrasts 153Ч155 163Ч165
Analysis of variance, univariate (ANOVA), unbalanced data, one-way model 153Ч155
Analysis of variance, univariate (ANOVA), unbalanced data, two-way model 160Ч168
Analysis of variance, univariate (ANOVA), unbalanced data, two-way model, constrained model 165Ч168
anova see УAnalysis of variance univariateФ
Apparent error rate see УError rate(s)Ф
Apple data 197
Association, measures of 289
Beetle data 118
Behrens Ч Fisher problem 99Ч104
Behrens Ч Fisher problem, multivariate 100Ч104
Behrens Ч Fisher problem, univariate 99Ч100
Biochemical data, full 199
Biochemical data, partial 192
Bonferroni critical values 78 144
Bonferroni critical values, table 421Ч422
Calcium data 69
Canonical correlation(s) 190 312Ч336
Canonical correlation(s) and discriminant analysis 312
Canonical correlation(s) and eigenvalues 314Ч316 323
Canonical correlation(s) and MANOVA 312 333
Canonical correlation(s) and measures of association 289
Canonical correlation(s) and multiple correlation 314 319
Canonical correlation(s), canonical variates see УCanonical variatesФ
Canonical correlation(s), definition of 313
Canonical correlation(s), influence 333
Canonical correlation(s), properties of 317Ч320
Canonical correlation(s), redundancy analysis 331Ч333
Canonical correlation(s), redundancy analysis, robust estimators 333
Canonical correlation(s), singular value decomposition 315Ч316
Canonical correlation(s), tests of significance 320Ч326
Canonical correlation(s), tests of significance and test of overall regression 321 323
Canonical correlation(s), tests of significance, Lawley Ч Hotelling test 323
Canonical correlation(s), tests of significance, likelihood ratio test (WilksТ A) 321Ч323
Canonical correlation(s), tests of significance, PillaiТs test 323
Canonical correlation(s), tests of significance, RoyТs test 323
Canonical correlation(s), tests of significance, subset of canonical correlations 324Ч326
Canonical correlation(s), tests of significance, test of independence 320Ч321
Canonical correlation(s), tests of significance, union-intersection test (RoyТs) 324
Canonical correlation(s), validation 326Ч327
Canonical correlation(s), validation, cross validation 326Ч327
Canonical correlation(s), validation, jackknife 327
Canonical variates 313 317Ч320 326Ч333
Canonical variates and eigenvectors 313Ч320 327
Canonical variates, canonical ridge weights 327
Canonical variates, common canonical variates 333
Canonical variates, definition of 313
Canonical variates, influence 333
Canonical variates, interpretation 328Ч331
Canonical variates, interpretation, correlations (structure coefficients) 329Ч331
Canonical variates, interpretation, rotation 328
Canonical variates, interpretation, standardized coefficients 328
Canonical variates, nonlinear canonical variates 333
Canonical variates, properties of 320
Canonical variates, redundancy analysis 331Ч333
Canonical variates, robust estimators 333
Canonical variates, scaling 317
Canonical variates, standardized coefficients 319
categorical data 255 262 266 306Ч307
Centering matrix 9Ч10
Central Limit Theorem (Multivariate) 53
Characteristic roots see УEigenvaluesФ
Chi-square distribution 48Ч49 53Ч54 60
Cholesky decomposition 42 408
Classification analysis (allocation) 230Ч265
Classification analysis (allocation) and discriminant analysis 201
Classification analysis (allocation) for categorical data 262
Classification analysis (allocation), assigning a sampling unit to a group 230
Classification analysis (allocation), assumptions 234
Classification analysis (allocation), assumptions, robustness to departures from 234
Classification analysis (allocation), correct classification rates 240
Classification analysis (allocation), costs of misclassification 233
Classification analysis (allocation), density estimation 263
Classification analysis (allocation), discriminant functions used in classification 232 239
Classification analysis (allocation), error rates 240Ч247 (see also УError rate(s)Ф)
Classification analysis (allocation), influence of individual observations 262
Classification analysis (allocation), logistic classification 254Ч259
Classification analysis (allocation), logistic classification for several groups 258
Classification analysis (allocation), logistic classification, comparison with linear classification 256Ч257
Classification analysis (allocation), logistic classification, quadratic logistic classification 258
Classification analysis (allocation), missing data 262Ч263
Classification analysis (allocation), nearest neighbor method 263
Classification analysis (allocation), posterior probabilities 234 236Ч237
Classification analysis (allocation), prior probabilities 230 236 238
Classification analysis (allocation), probit classification 259Ч261
Classification analysis (allocation), ridge classification 261
Classification analysis (allocation), robust classifications procedures 235
Classification analysis (allocation), several groups 236Ч239
Classification analysis (allocation), several groups, asymptotic optimality 236
Classification analysis (allocation), several groups, comparison of linear and quadratic rules 238Ч239
Classification analysis (allocation), several groups, linear classification function 236
Classification analysis (allocation), several groups, maximum likelihood rule 236
Classification analysis (allocation), several groups, optimal classification rule 236
Classification analysis (allocation), several groups, quadratic classification function 237Ч238
Classification analysis (allocation), several groups, regularized discriminant (classification) analysis 239
Classification analysis (allocation), subset selection 247Ч251
Classification analysis (allocation), subset selection with unequal covariance matrices 250Ч251
| Classification analysis (allocation), subset selection, using error rates 249Ч250
Classification analysis (allocation), subset selection, using stepwise discriminant analysis 247Ч249
Classification analysis (allocation), subset selection, using stepwise discriminant analysis, bias 251Ч254
Classification analysis (allocation), two groups 230Ч235
Classification analysis (allocation), two groups, asymptotic optimality 232
Classification analysis (allocation), two groups, linear classification rule 231Ч232
Classification analysis (allocation), two groups, maximum likelihood rule 230
Classification analysis (allocation), two groups, optimal classification rule 230
Classification analysis (allocation), two groups, quadratic classification rule 232Ч233
Coefficient of determination see У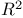 Ф Ф
Communality see УFactor analysis communalityФ
Condition number 20
Confidence interval(s) 74Ч79
Confidence interval(s) for linear combination(s) 74 92Ч94
Confidence interval(s) for regression coefficients 273Ч274
Confidence interval(s), Bonferroni intervals 77Ч79 94
Confidence interval(s), simultaneous intervals 75Ч76 93Ч95
Confidence region for  74 74
Confidence region for  93 93
Constant density ellipsoid 40Ч41
Contaminated normal 28
Contour Plot 40Ч42
Contrast matrix 84 163 166 169Ч170
Contrast(s) 84 95 142Ч148 150Ч151 153Ч160
Contrast(s) with unbalanced data 153Ч160
Contrast(s), Bonferroni procedure 144
Contrast(s), orthogonal 144 154
Contrast(s), Scheffe procedure 144Ч145
Contrast(s), simultaneous 150
Correct classification rate 240
Correlation matrix and factor analysis 379Ч380 383 385Ч386 389 392
Correlation matrix and principal components 342 344Ч347 349 351 353Ч359 364 367Ч370
Correlation matrix as standardized covariance matrix 1
Correlation matrix of linear combinations of variables 16
Correlation matrix, bias 12
Correlation matrix, population 11Ч12
Correlation matrix, relationship to covariance matrix 11Ч12
Correlation matrix, sample 11
Correlation matrix, test comparing two covariance matrices 138Ч140
Correlation of two linear combinations 15
Correlation of two random variables 6
Correlation, bias 6
Correlation, canonical see УCanonical correlation(s)Ф
Correspondence analysis 2 373
Covariance matrix (matrices) for one random vector 8Ч10
Covariance matrix (matrices) for two random vectors, 113
Covariance matrix (matrices), partitioned 12Ч13
Covariance matrix (matrices), pooled 87
Covariance matrix (matrices), population 10
Covariance matrix (matrices), positive definite 9Ч10
Covariance matrix (matrices), relationship to correlation matrix 11Ч12
Covariance matrix (matrices), sample 8Ч9
Covariance matrix (matrices), sample, distribution of 55
Covariance matrix (matrices), sample, unbiased 11
Covariance matrix (matrices), test for equality of 138Ч140
Covariance matrix (matrices), test for equality of table of critical values 446Ч447
Covariance of two linear combinations 15
Covariance of two random variables 5Ч6
Cross validation 244 326Ч327
Data matrix (Y) 7
Data, continuous 2
Data, discrete 2
Data, missing 23Ч27 (see also УMissing dataФ)
Density estimation 263
Density function 37Ч39
Determinant 409
Diabetes data 17
Diagonal matrix 11 400
Discriminant analysis (descriptive) 201Ч229 (see also УDiscriminant function(s)Ф)
Discriminant analysis (descriptive) and canonical correlation 312
Discriminant analysis (descriptive) and classification analysis 201
Discriminant analysis (descriptive) for two-way designs 210
Discriminant analysis (descriptive), assumptions 205Ч206
Discriminant analysis (descriptive), influence 206
Discriminant analysis (descriptive), ridge discriminant analysis 221Ч222
Discriminant analysis (descriptive), robust discriminant analysis 223Ч227
Discriminant analysis (descriptive), several groups 202Ч206
Discriminant analysis (descriptive), subset selection in higher order designs 218Ч219
Discriminant analysis (descriptive), subset selection, all possible subsets 218
Discriminant analysis (descriptive), subset selection, bias 219Ч221
Discriminant analysis (descriptive), subset selection, stepwise discriminant analysis 217Ч221
Discriminant analysis (descriptive), subset selection, using discriminant functions 217
Discriminant analysis (descriptive), tests of significance 207Ч210
Discriminant analysis (descriptive), two groups 201Ч202
Discriminant analysis (predictive) see УClassification analysisФ
Discriminant function(s) (descriptive) see also УDiscriminant analysis (descriptive)Ф
Discriminant function(s) (descriptive) for one group 74
Discriminant function(s) (descriptive) for two groups 92 201Ч202
Discriminant function(s) (descriptive) for two groups, effect of each variable 206Ч207
Discriminant function(s) (descriptive) for two groups, other estimators when  is near singular 221Ч222 is near singular 221Ч222
Discriminant function(s) (descriptive) for unbalanced data 157
Discriminant function(s) (descriptive), confidence intervals for 216
Discriminant function(s) (descriptive), interpretation of 210Ч215
Discriminant function(s) (descriptive), interpretation of correlations (structure coefficients) 211Ч215
Discriminant function(s) (descriptive), interpretation of partial F-tests 211
Discriminant function(s) (descriptive), interpretation of standardized coefficients 211
Discriminant function(s) (descriptive), invariance of 202
Discriminant function(s) (descriptive), plotting 216
Discriminant function(s) (descriptive), ridge estimator 221Ч222
Discriminant function(s) (descriptive), robust discriminant functions 223Ч227
Discriminant function(s) (descriptive), robust discriminant functions, for several groups (MANOVA) 128 151 202Ч206
Discriminant function(s) (descriptive), robust discriminant functions, other estimators when  is near singular 222 is near singular 222
Discriminant function(s) (descriptive), robust discriminant functions, properties 203
Discriminant function(s) (descriptive), standardized coefficients 206Ч207
Dispersion matrix see УCovariance matrixФ
Distance between two vectors (Mahalanobis) 22Ч23
E matrix 122 203
Eigenvalues 411Ч414
Eigenvalues and canonical correlations 314Ч316 323
Eigenvalues and discriminant functions 128 203Ч205 209 212Ч215 222Ч226
Eigenvalues and factor analysis 381Ч383
Eigenvalues and MANOVA 111
Eigenvalues and principal components 338 341
Eigenvectors 411Ч414
Eigenvectors and discriminant functions 203Ч204 210 212Ч213 222Ч225
Eigenvectors and factor analysis 381
Eigenvectors and principal components 338
Ellipsoid, constant density 40Ч41
Elliptically contoured distributions 56 112Ч113
EM algorithm 25Ч26
Error rate(s) 240Ч247
Error rate(s), actual error rate 240
Error rate(s), apparent correct classification rate 243Ч245
Error rate(s), apparent error rate 243Ч245
Error rate(s), apparent error rate, bias, correction for 244Ч247
Error rate(s), apparent error rate, bootstrap estimator 245
Error rate(s), apparent error rate, comparison of methods 245Ч247
Error rate(s), apparent error rate, cross validation 244
Error rate(s), apparent error rate, holdout method 244
Error rate(s), apparent error rate, leaving-one-out-method 244
Error rate(s), conditional error rate 240
Error rate(s), expected actual error rate 240
Error rate(s), experimentwise 2 82 95
Error rate(s), maximum likelihood estimator of 242
Error rate(s), optimum error rate 240Ч242
Error rate(s), plug-in estimator of error rate 240Ч243
Error rate(s), resubstitution 243
Error rate(s), true error rate 240
Estimation, least squares 267Ч268 281Ч282
Estimation, likelihood function 49
Estimation, maximum likelihood 49Ч52
Estimator, least squares 267Ч268 281Ч282
Estimator, maximum likelihood 49Ч52
Estimator, unbiased 2Ч3
Expected value of random matrix 10
Expected value of random vector [E(y)] 8
Expected value of sample covariance ![$[E(s_{xy})]$](/math_tex/8b27e7ed2d06922d73d127c04b4cefdc82.gif) 6 6
Expected value of sample covariance matrix [F(S)] 11
Expected value of sample mean ![$[E(\bar{y})]$](/math_tex/7c1e20782f974ca87f65e8521acd732582.gif) 2 2
Expected value of sample mean vector ![$[E(\bar{y})]$](/math_tex/7c1e20782f974ca87f65e8521acd732582.gif) 8 8
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -tests
-tests 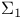 ,
, 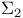
 known
known 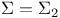

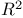 Ф
Ф

![$[E(s_{xy})]$](/math_tex/8b27e7ed2d06922d73d127c04b4cefdc82.gif)
![$[E(\bar{y})]$](/math_tex/7c1e20782f974ca87f65e8521acd732582.gif)