|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heath T.L. (ed.) Ч Thirteen Books of Euclid's Elements, Vol. 3 |
|
|
 |
| ѕредметный указатель |
"Abthiniathus" (or "Anthisathus") I. 203
"Anthisathus" (or "Abthiniathus") I. 203
"Aqaton" I. 88
"Axiom of Archimedes" III. 15Ч16
"Axiom of Archimedes", already used by Eudoxus III. 15
"Axiom of Archimedes", already used by Eudoxus, and mentioned by Aristotle III. 16
"Axiom of Archimedes", relation of, to Eucl. X. 1 III. 15Ч16
"Cause", cause = middle term (Aristotle) I. 149
"Cause", consideration of, omitted by commentators I. 19 45
"Cause", definition should state cause (Aristotle) I. 149
"Cause", question whether geometry should investigate cause (Geminus) I. 45 150n.
"Chance equimultiples" in phrase "other, chance, equimultiples" II. 143Ч144
"Composite to one another" (of numbers) II. 286Ч287
"Diagonal" numbers see ""Side-" and "diagonal-" numbers"
"Dissimilarly ordered" proportion in Archimedes = "perturbed proportion" II. 136
"Gnomon-wise", old name for perpendicular I. 36 181 272
"GooseТs foot" (pes anseris), name for Eucl. III. 7 I. 99
"Heavy and Light" tract on I. 18
"Heromides" I. 158
"Herundes" I. 156
"Iflaton" I. 88
"Mixed" (lines) I. 161Ч162
"Mixed" (lines), (surfaces) I. 162 170
"Mixed" (lines), different meanings of "mixed" I. 162
"Ordered" proportion, interpolated definition of II. 137
"Parallelepipedal" = with parallel planes or faces, "parallelepipedal solid" (not "solid parallelepiped") or "parallelepiped" III. 326
"Parallelepipedal" = with parallel planes or faces, "parallelepipedal" (solid) numbers in Nicomachus have two of sides differing by unity II. 290
"Parallelepipedal" = with parallel planes or faces, generally has six faces but sometimes more ("parallelepipedal prism") III. 401 404
"Peacock's tail", name for Eucl. III. 8 I. 99
"Perfect" (of a class of numbers) II. 293Ч294 421Ч425 III.
"Perfect" (of a class of numbers), 3 also called "perfect" II. 294
"Perfect" (of a class of numbers), Pythagoreans applied term to 10 II. 294
"Plane loci" I. 329Ч330
"Plane loci", Plane Loci of Apollonius I. 14 259 330 II.
"Plane problems" I. 329
"Platonic" figures I. 2 III.
"Platonic" figures, scholium on III. 438
"Quindecagon" (fifteen-angled figure), useful for astronomy II. 111
"Rule of three" Eucl. VI. 12 equivalent to II. 215
"Side of a medial minus a medial area" (in Euclid "that which produces with a medial area a medial whole"), a compound irrational straight line, biquadratic of which it is a root III. 7
"Side of a medial minus a medial area" (in Euclid "that which produces with a medial area a medial whole"), a compound irrational straight line, defined III. 165Ч166
"Side of a medial minus a medial area" (in Euclid "that which produces with a medial area a medial whole"), a compound irrational straight line, equivalent to square root of sixth apotome III. 209Ч211
"Side of a medial minus a medial area" (in Euclid "that which produces with a medial area a medial whole"), a compound irrational straight line, uniquely formed III. 174Ч177
"Side of a medial minus a rational area" (in Euclid "that which produces with a rational area a medial whole"), a compound irrational straight line, biquadratic of which it is a root III. 7
"Side of a medial minus a rational area" (in Euclid "that which produces with a rational area a medial whole"), a compound irrational straight line, defined III. 164
"Side of a medial minus a rational area" (in Euclid "that which produces with a rational area a medial whole"), a compound irrational straight line, equivalent to square root of fifth apotome III. 206Ч208
"Side of a medial minus a rational area" (in Euclid "that which produces with a rational area a medial whole"), a compound irrational straight line, uniquely formed III. 173Ч174
"Side of a rational plus a medial area," a compound irrational straight line, biquadratic equation of which it is a root III. 7
"Side of a rational plus a medial area," a compound irrational straight line, defined III. 88Ч89
"Side of a rational plus a medial area," a compound irrational straight line, equivalent to square root of fifth binomial III. 84 128Ч129
"Side of a rational plus a medial area," a compound irrational straight line, uniquely divided III. 99
"Side of the sum of two medial areas," a compound irrational straight line, biquadratic of which it is a root III. 7
"Side of the sum of two medial areas," a compound irrational straight line, defined III. 89Ч91
"Side of the sum of two medial areas," a compound irrational straight line, equivalent to square root of sixth binomial III. 84 130Ч131
"Side of the sum of two medial areas," a compound irrational straight line, uniquely divided III. 99Ч101
"Side" used in translation of Book X., "side of a square equal to (the area)" III. 13 119
"Side-"and "diagonal-" numbers, described I. 398Ч400
"Side-"and "diagonal-" numbers, described, connexion with Eucl. II. 9, 10 I. 398Ч400
"Side-"and "diagonal-" numbers, described, due to Pythagoreans I. 400 III. 20
"Side-"and "diagonal-" numbers, described, use for approximation to 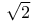 I. 399 I. 399
"Similar" (=equal) angles I. 182 252
"Similarly inclined" (of planes) III. 260 265
"Solid loci" I. 329 330
"Solid loci", Solid Loci of Aristaeus I. 16 329
"Solid problems" I. 329 330
'Ali b. Ahmad Abu 'l Qasim al-Antaki I. 86
Abu 'Abdallah Muh. b. Mu'adh al-Jayyani I. 90
Abu 'Ali al-Basri I. 88
Abu 'Ali al-Hasan b. al-Hasan b. al-Haitham I. 88 89
Abu 'I 'Abbas al-Fadl b. Hatim see "an-Nairizi"
Abu 'l Wafa al-Buzjani I. 77 85 86
Abu 'Uthman ad-Dimashqi I. 25 77
Abu Da'ud Sulaiman b. 'Uqba I. 85 90
Abu Ja'far al-Khazin I. 77 85
Abu Ja'far Muh. b. Muh. b. al-Hasan Nasiraddin at-Tusi see "Nasiraddin"
Abu Muh. al-Hasan b. 'Ubaidallah b. Sulaiman b. Wahb I. 87
Abu Muh. b. AbdalbaqI al-Bagdadi al-Faradi I. 8n. 90
Abu Nasr Gars al-Na'ma I. 90
Abu Nasr Mansur b. 'Ali b. 'Iraq I. 90
Abu Nasr Muh. b. Muh. b. Tarkhan b. Uzlag al-Farabi I. 88
Abu Sa'id Sinan b. Thabit b. Qurra I. 88
Abu Sahl Wijan b. Rustam al-Kuhi I. 88
Abu Yusuf Ya'qub b. Ishaq b. as-Sabbah al-Kindi I. 86
Abu Yusuf Ya'qub b. Muh. ar-Razi I. 86
Adjacent, meaning I. 181
Adrastus II. 292
Aenaeas (or Aigeias) of Hierapolis I. 28 311
Aganis I. 27Ч28 191
Ahmad b. 'Umar al-Karabisi I. 85
Ahmad b. al-Husain al-Ahwazi al-Katib I. 89
Aigeias (?Aenaeas) of Hierapolis I. 28 311
al-'Abbas b. Sa'id al-Jauhari I. 85
al-Ahwazi I. 89
al-Antaki I. 86
al-Arjani, Ibn Rahawaihi I. 86
Al-Biruni I. 90
al-Faradi I. 8n. 90
al-Haitham I. 88 89
al-Hajjaj b. Yusuf b. Matar, translator of the Elements I. 22 75 76 79 80 83 84
al-Hasan b. 'Ubaidallah b. Sulaiman b. Wahb I. 87
al-Jauhari, al-'Abbas b. Sa'id I. 85
al-Jayyani I. 90
al-KarabisI I. 85
al-Khazin, Abu Ja'far I. 77 85
al-Kindi I. 5n. 86
al-Kuhi I. 88
al-Ma'mun, Caliph I. 75
Al-Mahani I. 85
al-Mansur, Caliph I. 75
al-Musta'sim, Caliph I. 90
al-Mutawakkil, Caliph I. 75
al-Qifti I. 4n. 94
Alcinous II. 98
Alexander Aphrodisiensis I. 7n. 29 II.
Algebra, geometrical I. 372Ч374
Algebra, geometrical, algebraical equivalents of propositions in Book II. I. 372Ч373
Algebra, geometrical, classical method was that of Eucl. II. I. 373 see
Algebra, geometrical, equivalents in Book X. of propositions in algebra, 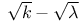 cannot be equal to k' III. 58Ч60 cannot be equal to k' III. 58Ч60
Algebra, geometrical, geometrical equivalents of algebraical operations I. 374
Algebra, geometrical, if 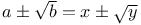 , then a=x, b=y III. 93Ч94 167Ч168 , then a=x, b=y III. 93Ч94 167Ч168
Algebra, geometrical, preferable to semi-algebraical method I. 377Ч378
Algebra, geometrical, semi-algebraical method due to Heron I. 373
Algebra, geometrical, semi-algebraical method due to Heron, and favoured by Pappus I. 373
Allman, G.J. I. 135n. 318 352 III. 439
Alternate, (of angles) I. 308
Alternate, (of ratios), alternately II. 134
Alternative proofs, interpolated I. 58 59 II. 23Ч24 III. 10
Amaldi, Ugo I. 175 179Ч180 193 201 313 328 II. 126
Ambiguous case I. 306Ч307
Ambiguous case in VI. 7 II. 208Ч209
Amphinomus I. 125 128 150n.
Amyclas of Heraclea I. 117
An-Nairizi, Abu 'l 'Abbas al-Fadl b. Hatim I. 21Ч24 85 184 190 191 195 223 232 258 270 285 299 303 326 364 367 369 373 405 408 II. 16 28 34 36 44 47 302 320 383
Analysis (and synthesis) I. 18
Analysis (and synthesis), analysis and synthesis of problems I. 140Ч142
Analysis (and synthesis), analysis should also reveal conditions of possibility I. 142
Analysis (and synthesis), definitions of, interpolated I. 138 III.
Analysis (and synthesis), described by Pappus I. 138Ч139
Analysis (and synthesis), example from Pappus I. 141Ч142
Analysis (and synthesis), interpolated alternative proofs of XIII. 1-5 by analysis and synthesis I. 137 III.
Analysis (and synthesis), method of analysis and precautions necessary to I. 139Ч140
Analysis (and synthesis), modern studies of Greek analysis I. 139
Analysis (and synthesis), mystery of Greek analysis III. 246
Analysis (and synthesis), theoretical and problematical analysis I. 138
Analysis (and synthesis), Treasury of Analysis I. 8 10 11 138
Analysis (and synthesis), two parts of analysis (a) transformation, (b) resolution, and two parts of synthesis, (a) construction, (b) demonstration I. 141
Analytical method I. 36
Analytical method, supposed discovery of, by Plato I. 134 137
Anaximander I. 370 II.
Anaximenes II. 111
| Anchor-ring I. 163
Andron I. 126
Angle, adjacent angles I. 181
Angle, alternate I. 308
Angle, angle as cluster of straight lines or rays I. 180Ч181
Angle, angle as cluster of straight lines or rays, defined by Veronese I. 180
Angle, angle in a semicircle, theorem of I. 317Ч319
Angle, angle of a segment I. 253 II.
Angle, angle of a semicircle I. 182 253 II.
Angle, angles not less than two right angles not recognised as angles II. 47Ч49 see "Proclus" "Zenodorus"
Angle, Apollonius' view of, as contraction I. 176 177
Angle, Aristotle's notion of angle as I. 176
Angle, as part of a plane ("angular sector") I. 179Ч180
Angle, classification of angles (Geminus) I. 178Ч179
Angle, construction by Apollonius of angle equal to angle I. 296
Angle, controversies about "angle of semicircle" and hornlike angle II. 39Ч42
Angle, curvilineal and "mixed" angles I. 26 178Ч179
Angle, curvilineal and "mixed" angles, horn-like I. 177 178 182 265 II. 39 40
Angle, curvilineal and "mixed" angles, lune-like I. 26 178Ч179
Angle, curvilineal and "mixed" angles, scraper-like I. 178
Angle, Curvilineal and rectilineal, Euclid's definition of I. 176sq.
Angle, definition criticised by Syrianus I. 176
Angle, definitions of angle classified I. 179
Angle, did Euclid extend "angle" to angles greater than two right angles in VI. 33? II. 275Ч276
Angle, dihedral angle III. 264Ч265
Angle, exterior and interior (to a figure) I. 263 280
Angle, exterior when re-entrant I. 263
Angle, exterior when re-entrant, in which case we have a hollow-angled figure I. 27 188 II.
Angle, flat angle (Veronese etc.) I. 180Ч181 269
Angle, interior and opposite I. 280
Angle, Plutarch and Carpus on I. 177
Angle, recent Italian views I. 179Ч181
Angle, relation, Euclid I. 178
Angle, similar(=equal) I. 178 182 252
Angle, solid angle III. 261 267Ч268
Angle, Syrianus' compromise I. 178
Angle, three kinds of angles, which is prior (Aristotle)? I. 181Ч182
Angle, to which category does it belong? quale, Aristotle and Eudemus I. 177Ч178
Angle, to which category does it belong? quantum, Plutarch, Carpus, "Aganis" I. 177
Angle, to which category does it belong? quantum, Plutarch, Carpus, "Aganis", Euclid I. 178
Angle, treatise on the Angle by Eudemus I. 34 38 177Ч178
Angle, trisection of angle, by conchoid of Nicomedes I. 265Ч266
Angle, trisection of angle, by quadratrix of Hippias I. 266
Angle, trisection of angle, by spiral of Archimedes I. 267
Angle, vertical I. 278
Annex = the straight line which, when added to a compound irrational straight line formed by subtraction, makes up the greater "term," i.e. the negative "term" III. 159
Antecedents (leading terms in proportion) II. 134
Antiparallels may be used for construction of VI. 12 II. 215
Antiphon I. 7n. 35
Apastamba-Sulba-Sutra I. 352
Apastamba-Sulba-Sutra, approximation to 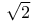 and Thibaut's explanation I. 361 363Ч364 and Thibaut's explanation I. 361 363Ч364
Apastamba-Sulba-Sutra, Buerk's claim that Indians had discovered the irrational I. 363Ч364
Apastamba-Sulba-Sutra, evidence in, as to early discovery of Eucl. I. 47 and use of gnomon I. 360Ч364
Apastamba-Sulba-Sutra, inaccurate values of  in I. 364 in I. 364
Apollodorus "Logisticus" I. 37 319 351
Apollonius I. 138 188 221 222 246 259 370 373 II. 190 258 III. 267
Apollonius on "unordered" irrationals I. 42 115 III. 10 246 255Ч259
Apollonius on elementary geometry I. 42
Apollonius on parallel-axiom (?) I. 42Ч43
Apollonius on the angle I. 176
Apollonius on the cochlias I. 34 42 162
Apollonius on the line I. 159
Apollonius, a "carpenter" I. 5
Apollonius, adaptation to conics of theory of application of areas I. 344Ч345
Apollonius, comparison of dodecahedron and icosahedron I. 6 III. 512 513
Apollonius, constructions by, for a perpendicular I. 270
Apollonius, constructions by, for an angle equal to an angle I. 296
Apollonius, constructions by, for bisection of straight line I. 268
Apollonius, disparaged by Pappus in comparison with Euclid I. 3
Apollonius, general definition of diameter I. 325
Apollonius, general definition of oblique (circular) cone III. 270
Apollonius, geometrical algebra in I. 373
Apollonius, his "general treatise" I. 42
Apollonius, Plane I. 151
Apollonius, Plane Loci I. 14 259 330
Apollonius, Plane Loci, theorem from (arising out of Eucl. VI. 3), also found in Aristotle II. 198Ч200
Apollonius, Plane, lemma by Pappus on II. 64Ч65
Apollonius, Plane, problem from II. 81
Apollonius, supposed by some Arabians to be author of the Elements I. 5
Apollonius, tried to prove axioms I. 42 62 222Ч223
Apotome of a medial (straight line), first and second, and biquadratics of which they are roots III. 7
Apotome of a medial (straight line), first apotome of a medial, defined III. 159Ч160
Apotome of a medial (straight line), first apotome of a medial, equivalent to square root of second apotome III. 194Ч198
Apotome of a medial (straight line), first apotome of a medial, uniquely formed III. 168Ч169
Apotome of a medial (straight line), second apotome of a medial, defined III. 161Ч162
Apotome of a medial (straight line), second apotome of a medial, equivalent to square root of third apotome III. 199Ч202
Apotome of a medial (straight line), second apotome of a medial, uniquely formed III. 170Ч172
Apotome, apotome cannot be binomial also III. 240Ч242
Apotome, apotome equivalent to square root of first apotome III. 190Ч194
Apotome, biquadratic from which it arises III. 7
Apotome, compound irrational straight line (difference between two "terms") III. 7
Apotome, connected by Theaetetus with harmonic mean III. 3 4
Apotome, defined III. 158Ч159
Apotome, different from medial (straight line) and from other irrationals of same series with itself III. 242
Apotome, first, second, third, fourth, fifth and sixth apotomes equivalent to squares of apotome, first apotome of a medial etc. III. 212Ч229
Apotome, first, second, third, fourth, fifth and sixth apotomes, quadratics from which arising III. 5Ч6
Apotome, first, second, third, fourth, fifth and sixth apotomes, quadratics from which arising, and found respectively (X. 85-90) III. 178Ч190
Apotome, first, second, third, fourth, fifth and sixth apotomes, quadratics from which arising, defined III. 177
Apotome, uniquely formed III. 167Ч168
Apotome, used to rationalise binomial with proportional terms III. 243Ч248 252Ч254
Application of areas I. 36 343Ч345
Application of areas, adaptation to conics (Apollonius) I. 344Ч345
Application of areas, application contrasted with construction (Proclus) I. 343
Application of areas, complete method equivalent to geometrical solution of mixed quadratic equation I. 344Ч345 383Ч385 386Ч388 II. 258Ч260 263Ч265 266Ч267
Application of areas, contrasted with exceeding and falling-short I. 343
Approximations, 7/5 as approximation to 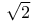 (Pythagoreans and Plato) II. 119 (Pythagoreans and Plato) II. 119
Approximations, approximations to 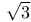 in Archimedes and (in sexagesimal fractions) in Ptolemy II. 119 in Archimedes and (in sexagesimal fractions) in Ptolemy II. 119
Approximations, remarkably close approximations (stated in sexagesimal fractions) in scholia to Book X. III. 523
Approximations, to  (Archimedes) II. 119 (Archimedes) II. 119
Approximations, to 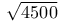 (Theon of Alexandria) II. 119 (Theon of Alexandria) II. 119
ar-Razi, Abu Yusuf Ya'qub b. Muh. I. 86
Arabian editors and commentators I. 75Ч90
Arabic numerals in scholia to Book X., 1th c. I. 71 III.
Archimedes I. 116 142 225 370 II. 190 III. 270 375 521
Archimedes on discovery by Eudoxus df method of exhaustion III. 365Ч366 374
Archimedes on plane I. 171Ч172
Archimedes on straight line I. 166
Archimedes, "Axiom" already used by Eudoxus and mentioned by Aristotle III. 16
Archimedes, "Axiom" of (called however "lemma," assumption, by A. himself) I. 234
Archimedes, "porisms" in I. 11n. 13
Archimedes, "postulates" in I. 120 123
Archimedes, application to area of parabolic segment III. 366Ч367
Archimedes, approximations to 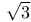 , square roots of large numbers and to , square roots of large numbers and to  II. 119 II. 119
Archimedes, extension of a proportion between commensurables to cover incommensurables II. 193
Archimedes, Liber assumptorum, proposition from II. 65
Archimedes, new fragment of, "method of Archimedes about mechanical theorems,", discovered by Heiberg and published and annotated by him and Zeuthen II. 40 III.
Archimedes, new fragment of, "method of Archimedes about mechanical theorems,", discovered by Heiberg and published and annotated by him and Zeuthen, adds new chapter to history of integral calculus, which the method actually is III. 366Ч367
Archimedes, proved by means of Dedekind's Postulate (Stolz) III. 16
Archimedes, relation of "Axiom" to X. 1 III. 15Ч16
Archimedes, spiral of Archimedes I. 26 267
Archytas I. 20
Archytas, proof that there is no numerical geometric mean between n and n + 1 II. 295
Areskong, M.E. I. 113
Arethas, Bishop of Caesarea I. 48
Arethas, Bishop of Caesarea, had famous Plato MS. of Patmos (Cod. Clarkianus) written I. 48
Arethas, Bishop of Caesarea, owned Bodleian MS. (B) I. 47Ч48
Argyrus, Isaak I. 74
Aristaeus I. 138
Aristaeus on conics I. 3
Aristaeus, comparison of five (regular solid) figures I. 6 III. 513
Aristaeus, Solid Loci I. 16 329
Aristotelian Problems I. 166 182 187
Aristotle I. 38 45 117 150n. 181 184 185 187 188 195 202 203 221 222 223 226 259 262Ч263 283 II. 4 22 79 112 135 149 159 160 165 184 188 189 III.
Aristotle on alternate ratios II. 134
Aristotle on attributes I. 319 320 325
Aristotle on axioms I. 119Ч121
Aristotle on composite numbers as plane and solid II. 286 288 290
Aristotle on def. of same ratio II. 120Ч121
Aristotle on definition by negation I. 156Ч157
Aristotle on definitions I. 117 119Ч120 143Ч144 146Ч150
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



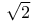
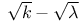 cannot be equal to k'
cannot be equal to k' 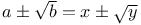 , then a=x, b=y
, then a=x, b=y  in
in 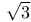 in Archimedes and (in sexagesimal fractions) in Ptolemy
in Archimedes and (in sexagesimal fractions) in Ptolemy 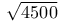 (Theon of Alexandria)
(Theon of Alexandria)