|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heath T.L. (ed.) Ч Thirteen Books of Euclid's Elements, Vol. 3 |
|
|
 |
| ѕредметный указатель |
Golden section (section in extreme and mean ratio), connexion with theory of irrationals I. 137 III.
Golden section (section in extreme and mean ratio), discovered by Pythagoreans I. 137 403 II.
Golden section (section in extreme and mean ratio), theorems of Eucl. XIII. 1-5 on, probably due to Eudoxus III. 441
Golden section (section in extreme and mean ratio), theory carried further by Plato and Eudoxus II. 99
Gow, James I. 135n.
Gracilis, Stephanus I. 101Ч102
Grandi, Guido I. 107
Greater ratio, arguments from greater to less ratios etc. unsafe unless they go back to original definitions (Simson on V. 10) II. 156Ч157
Greater ratio, EuclidТs criterion not the only one II. 130
Greater ratio, test for, cannot coexist with test for equal or less ratio II. 130Ч131
Greatest common measure, EuclidТs method of finding corresponds exactly to ours II. 118 299 III. 21Ч22
Greatest common measure, method used to prove incommensurability III. 18Ч19
Greatest common measure, method used to prove incommensurability, for this purpose often unnecessary to carry it far (cases of extreme and mean ratio and of  ) III. 18Ч19 ) III. 18Ч19
Greatest common measure, Nicomachus gives the same method II. 300
Gregory of St Vincent I. 401 404
Gregory, David I. 102Ч103 II. 143 III.
Gromatici I. 91n. 95
Grynaeus I. 100Ч101
Haebler, Th. II. 294n.
Halifax, William I. 108 110
Halliwell (Phillips) I. 95n.
Hankel, H. I. 139 141 232 234 344 354 II. 117 III.
Harmonica of Ptolemy, Comm. on I. 17
Harmony, Introduction to, not by Euclid I. 17
Harun ar-Rashid I. 75
Hauber, C.F. II. 244
Hauff, J.K.F. I. 108
Helix, cylindrical I. 161 162 329 330
Helmholtz I. 226 227
Henrici and Treutlein I. 313 404 II.
Henrion, Denis I. 108
Herigone, Pierre I. 108
Herlin, Christian I. 100
Hermotimus of Colophon I. 1
Herodotus I. 37n. 370
Heron of Alexandria I. 137n. 159 163 168 170 171Ч172 176 183 184 185 188 189 222 223 243 253 285 287 299 351 369 371 405 407 408 II. 16Ч17 24 28 33 34 36 44 47 48 116 189 302 320 383 395 III. 263 265 267 268 269 270 366 404 442
Heron of Alexandria, addition to I. 47 I. 366Ч368
Heron of Alexandria, apparently originated semi-algebraical method of proving theorems of Book II. I. 373 378
Heron of Alexandria, commentary on EuclidТs Elements I. 20Ч24
Heron of Alexandria, comparison of areas of triangles in I. 24 I. 334Ч335
Heron of Alexandria, direct proof of I. 25 I. 301
Heron of Alexandria, does not recognise angles equal to or greater than two right angles II. 47Ч48
Heron of Alexandria, Eucl. III. 12 interpolated from II. 28
Heron of Alexandria, extends III. 20, 21 to angles in segments less than semicircles II. 47Ч48
Heron of Alexandria, Heron and Vitruvius I. 20Ч21
Heron of Alexandria, mechanicus, date of I. 20Ч21 III.
Heron of Alexandria, proof of formula for area of triangle, 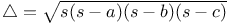 II. 87Ч88 II. 87Ч88
Heron, ProclusТ instructor I. 29
Hieronymus of Rhodes I. 305
Hilbert, D. I. 157 193 201 228Ч231 249 313 328
Hipparchus I. 4n. 30n. III.
Hippasus II. 97 III.
Hippias of Elis I. 42 265Ч266
Hippocrates of Chios I. 8n. 29 35 38 116 135 136n. 386Ч387 II.
Hippocrates of Chios, first proved that circles (and similar segments of circles) are to one another as the squares on their diameters III. 366 374
Hippopede, a certain curve used by Eudoxus I. 162Ч163 176
Hoffmann, Heinrich I. 107
Hoffmann, Joh.Jos.Ign. I. 108 365
Holgate, T.F. III. 284 303 331
Holtzmann, Wilhelm (Xylander) I. 107
Homoeomeric (uniform) lines I. 40 161 162
Hoppe, E. I. 21 III.
Hornlike angle I. 177 178 182 265 II. 40
Hornlike angle of Cardano (quantities of different orders or kinds), of Peletier (hornlike angle no angle, no quantity, nothing; angles of all semicircles right angles and equal) II. 41
Hornlike angle of Clavius II. 42
Hornlike angle of Vieta and Galileo ("angle of contact no angle") II. 42
Hornlike angle of Wallis (angle of contact not inclination at all but degree of curvature) II. 42
Hornlike angle, Democritus may have written on hornlike angle II. 40
Hornlike angle, hornlike angle and angle of semicircle, controversies on II. 39Ч42
Hornlike angle, Proclus on II. 39Ч40
Hornlike angle, view of Campanus ("not angles in same sense") II. 41
Horsley, Samuel I. 106
Houeel, J. I. 219
Hudson, John I. 102
Hultsch, F. I. 20 329 400 II. III. 522 523 526 527
Hunain b. Ishaq al-'Ibadi I. 75
Hypotheses, confused by Proclus with definitions I. 121Ч122
Hypotheses, geometer's hypotheses not false (Aristotle) I. 119
Hypotheses, in Aristotle I. 118Ч120
Hypotheses, in Plato I. 122
Hypothetical construction I. 199
Hypsicles I. 5
Hypsicles, author of Book XIV. I. 5 6 III. 512
Iamblichus I. 63 83 II. 116 279 280 281 283 284 285 286 287 288 289 290 291 292 293 419 III.
Ibn al-'Amid I. 86
Ibn al-Haitham I. 88 89
Ibn al-Lubudi I. 90
Ibn Rahawaihi al-Arjani I. 86
Ibn Sina (Avicenna) I. 77 89
icosahedron II. 98
Icosahedron, defined III. 262
Icosahedron, discovery of, attributed to Theaetetus III. 438
Icosahedron, Mr H.M. Taylor's construction III. 491Ч492
Icosahedron, problem of inscribing in sphere, Euclid's solution III. 481Ч489
Icosahedron, problem of inscribing in sphere, Pappus' solution III. 489Ч491
Inclination of plane to plane (= dihedral angle) III. 260 264
Inclination of straight line to plane, defined III. 260 263Ч264
Incommensurables, approximations to  II. 119 II. 119
Incommensurables, approximations to  by means of sexagesimal fractions III. 523 by means of sexagesimal fractions III. 523
Incommensurables, approximations to  by means of side- and diagonal-numbers I. 399Ч401 II. by means of side- and diagonal-numbers I. 399Ч401 II.
Incommensurables, approximations to 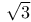 II. 119 III. II. 119 III.
Incommensurables, approximations to 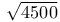 by means of sexagesimal fractions II. 119 by means of sexagesimal fractions II. 119
Incommensurables, discovered by Pythagoras or Pythagoreans III. 1 2 3
Incommensurables, discovered by Pythagoras or Pythagoreans, and with reference to  I. 351 III. 2 19 I. 351 III. 2 19
Incommensurables, incommensurable a natural kind, unlike irrational which depends on convention or assumption (Pythagoreans) III. 1
Incommensurables, incommensurable in length and incommensurable in square defined III. 10 11
Incommensurables, means of expression consist in power of approximation without limit (De Morgan) II. 119
Incommensurables, method of testing incommensurability (process of finding G.C.M.) II. 118 III.
Incommensurables, proof of incommensurability of  no doubt Pythagorean III. 2 no doubt Pythagorean III. 2
Incommensurables, proof of incommensurability of  no doubt Pythagorean, proof in Chrystal's Algebra III. 19Ч20 no doubt Pythagorean, proof in Chrystal's Algebra III. 19Ч20
Incommensurables, symbols for, used in notes III. 34
Incomposite, (of lines) I. 160Ч161
Incomposite, (of number) = prime II. 284
Incomposite, (of surfaces) I. 170
Indivisible lines, theory of, rebutted I. 268
Infinite, Aristotle on the I. 232Ч234
Infinite, infinite division not assumed, but proved, by geometers I. 268
Infinity, parallels meeting at I. 192Ч193
Ingrami, G. I. 175 193 195 201 227Ч228 II. 126
Integral calculus, in new fragment of Archimedes III. 366Ч367
Interior and exterior (of angles) I. 263 280
Interior and exterior (of angles), interior and opposite angle I. 280
Interpolations in the Elements before Theon's time I. 58Ч63
Interpolations in the Elements by Theon I. 46 55Ч56
Interpolations in the Elements, cases in XI. 23 III. 319Ч321
Interpolations in the Elements, defs. of analysis and synthesis, and proofs of XIII. 1-5 by III. 442Ч443
Interpolations in the Elements, Eucl. I. 40 interpolated I. 338
Interpolations in the Elements, other propositions interpolated, (III. 12) II. 28
Interpolations in the Elements, other propositions interpolated, (III. 12), (proposition after XI. 37) III. 360
Interpolations in the Elements, other propositions interpolated, (XIII. 6) III. 449Ч451
Inverse (ratio), inversely II. 134
Inverse (ratio), inversely, inversion is subject of V. 4, Por. (Theon) II. 144
Inverse (ratio), inversely, inversion is subject of V. 4, Por. (Theon), and of V. 7, Por. II. 149
Inverse (ratio), inversely, inversion is subject of V. 4, Por. (Theon), and of V. 7, Por., but is not properly put in either place II. 149
Inverse (ratio), inversely, Simson's Prop. B on, directly deducible from V. Def. 5 II. 144
Irrational, "irrational diameter of 5" (Pythagoreans and Plato) I. 399Ч400 III.
Irrational, actual use of Euclid's irrationals in Greek geometry III. 9Ч10
Irrational, an irrational straight line is so relatively to any straight line taken as rational III. 10 11
Irrational, approximation to  by means of "side-" and "diagonal-" numbers I. 399Ч401 II. by means of "side-" and "diagonal-" numbers I. 399Ч401 II.
Irrational, Book X. a repository of results of solution of different types of quadratic and biquadratic equations III. 5
Irrational, claim of India to priority of discovery I. 363Ч364
Irrational, compound irrationals in Book X. all different III. 242Ч243
Irrational, depends on assumption or convention, unlike incommensurable which is a natural kind (Pythagoreans) III. 1
Irrational, discovered by Pythagoras or Pythagoreans I. 351 III. 3
Irrational, discovered by Pythagoras or Pythagoreans, and with reference to  I. 351 III. 2 19 III. I. 351 III. 2 19 III.
Irrational, Euclid's irrationals, object of classification of III. 4 5
Irrational, Indian approximation to  I. 361 363Ч364 I. 361 363Ч364
Irrational, irrational area incommensurable with rational area or square on rational straight line III. 10 12
Irrational, irrational ratio I. 137
Irrational, types of equations of which Euclid's irrationals are positive roots III. 5Ч7
| Irrational, unordered irrationals (Apollonius) I. 42 115 III. 10 246 255Ч259
Isaacus Monachus (or Argyrus) I. 73Ч74 407
Ishaq b. Hunain b. Ishaq al-'Ibadi, Abu Ya'qub, translation of Elements by I. 75Ч80 83Ч84
Isidorus of Miletus III. 520
Isma'il b. Bulbul I. 88
Isoperimetric (or isometric) figures, Pappus and Zenodorus on I. 26 27 333
Isosceles I. 187
Isosceles of numbers (= even) I. 188
Isosceles, isosceles right-angled triangle I. 352
Isosceles, isosceles triangle of IV. 10, construction of, due to Pythagoreans II. 97Ч99
Jacobi, C.F.A. II. 188
Jakob b. Machir I. 76
Joannes Pediasimus I. 72Ч73
Johannes of Palermo III. 8
Junge, G., on attribution of theorem of I. 47 and discovery of irrationals to Pythagoras I. 351 III. 523
Kaestner, A.G. I. 78 97 101
Katyayana Sulba-Sutra I. 360
Keill, John I. 105 110Ч111
Kepler I. 193
Killing, W. I. 194 219 225Ч226 235 242 272 III.
Klamroth, M. I. 75Ч84
Kluegel, G.S. I. 212
Kluge III. 520
Knesa, Jakob I. 112
Knoche I. 32n. 33n. 73
Kroll, W. I. 399Ч400
Lachlan, R. II. 226 227 245Ч246 247 256 272
Lambert, J.H. I. 212Ч213
Lardner, Dionysius I. 112 246 250 298 404 II. 259 271
Lascaris, Constantinus 3
Leading theorems (as distinct from converse) I. 257
Leading theorems (as distinct from converse), leading variety of conversion I. 256Ч257
Least common multiple II. 336Ч341
Leeke, John I. 110
Lefevre, Jacques I. 100
Legendre, Adrien Marie I. 112 169 213Ч219 II. III. 264 265 266 267 268 273 275 298 309 356 436
Legendre, Adrien Marie on equivalent parallelepipeds III. 335Ч336
Legendre, Adrien Marie, alternative proofs of theorems relating to prisms III. 331Ч333
Legendre, Adrien Marie, definition of planes at right angles III. 303
Legendre, Adrien Marie, proof of Eucl. XI. 15 III. 299
Legendre, Adrien Marie, proof of Eucl. XI. 19 III. 305
Legendre, Adrien Marie, proof of Eucl. XI. 4 III. 280
Legendre, Adrien Marie, proof of Eucl. XI. 6, 8 III. 284 289
Legendre, Adrien Marie, proof of Eucl. XII. 2 III. 377Ч378
Legendre, Adrien Marie, propositions on volumes of cylinders and cones III. 422Ч423
Legendre, Adrien Marie, propositions on volumes of pyramids III. 389Ч391
Legendre, Adrien Marie, proves VI. 1 and similar propositions in two parts (1) for commensurables, (2) for incommensurables II. 193Ч194
Leibniz I. 145 169 176 194
Leiden MS. 399, 1 of al-Hajjaj and an-Nairizi I. 22
Lemma I. 114
Lemma, alternative propositions on duplicate ratios and ratios of which they are duplicate (De Morgan and others) II. 242Ч247
Lemma, lemma assumed in VI. 22 II. 242Ч243
Lemma, lemmas interpolated I. 59Ч60
Lemma, lemmas interpolated, (after X. 59) III. 97 131Ч132
Lemma, lemmas interpolated, (after X. 9) III. 30Ч31
Lemma, lemmas interpolated, especially from Pappus I. 67
Lemma, lemmas suspected, (that after XII. 2) III. 375
Lemma, lemmas suspected, (that after XIII. 2) III. 444Ч445
Lemma, lemmas suspected, (those added to X. 18, 23) III. 48
Lemma, meaning (=assumption) I. 133Ч134
Length (of numbers in one dimension) II. 287
Length (of numbers in one dimension), Plato restricts term to side of complete square II. 287
Leodamas of Thasos I. 36 134
Leon I. 116
Leonardo of Pisa III. 8
Leotaud, Vincent II. 42
Linderup, H.C. I. 113
Line, "asymptotic" or non-secant, secant I. 161
Line, "divisible or continuous one way" (Aristotle) I. 158Ч159
Line, "flux of point" I. 159
Line, "magnitude extended one way" (Aristotle, "Heromides") I. 158
Line, Apollonius on I. 159
Line, classification of lines, Geminus, first classification I. 160Ч161
Line, classification of lines, Geminus, second classification I. 161
Line, classification of lines, Heron I. 159Ч160
Line, classification of lines, Plato and Aristotle I. 159Ч160
Line, composite, incomposite, "forming a figure", determinate, indeterminate) I. 160
Line, homoeomeric (uniform) I. 161Ч162
Line, loci on lines I. 329 330
Line, objection of Aristotle I. 158
Line, Platonic definition I. 158
Line, Proclus on lines without extremities I. 165
Line, simple, "mixed" I. 161Ч162
Line, straight, curved, circular, spiral-shaped, bent, broken, round I. 159
Linear, loci I. 330
Linear, loci, numbers = (1) in one dimension II. 287
Linear, loci, numbers = (2) prime II. 285
Linear, loci, problems I. 330
Lionardo da Vinci, proof of I. 47 I. 365Ч366
Lippert I. 88n.
Lobachewsky, N.I. I. 174Ч175 213 219
Locus-theorems and loci, corresponding distinction between plane and solid problems, to which Pappus adds linear problems I. 330
Locus-theorems and loci, further distinction in Pappus I. 330
Locus-theorems and loci, loci likened by Chrysippus to Platonic ideas I. 330Ч331
Locus-theorems and loci, locus defined by Proclus I. 329
Locus-theorems and loci, locus-theorems and loci (1) on lines (a) plane loci (straight lines and circles) (b) solid loci (conics), (2) on surfaces I. 329
Locus-theorems and loci, Proclus regards locus in I. 35, III. 21, 31 as an area which is locus of area (parallelogram or triangle) I. 330
Logical conversion, distinct from geometrical I. 256
Logical deductions I. 256 284Ч285 300
Logical deductions, logical equivalents I. 309 314Ч315
Logical deductions, not made by Euclid II. 22 29
Lorenz, J.F. I. 107Ч108 III.
Loria, Gino I. 7n. 10n. 11n. 12n. III. 9 527
Luca Paciuolo I. 98Ч99 100 III.
Lucas, E. III. 527
Lucian II. 99
Lundgren, F.A.A. I. 113
Machir, Jakob b. I. 76
Magni, Domenico I. 106
Magnitude, common definition vicious I. 148
Major (irrational) straight line, biquadratic of which it is positive root III. 7
Major (irrational) straight line, defined III. 87Ч88
Major (irrational) straight line, equivalent to square root of fourth binomial III. 84 125Ч127
Major (irrational) straight line, extension of meaning to irrational straight line of three terms III. 258
Major (irrational) straight line, uniquely divided III. 98
Mansion, P. I. 219
Manuscripts of Elements I. 46Ч51
Martianus Capella I. 91 155
Martin, T.H. I. 20 29n. 30n.
Mas'ud b. al-Qass al-Bagdadi I. 90
Maximus Planudes, scholia and lectures on Elements I. 72
Means, geometric mean is "proportion par excellence" II. 292Ч293
Means, no numerical geometric mean between n and n + 1 (Archytas and Euclid) II. 294Ч295
Means, one geometric mean between similar plane numbers, two between similar solid numbers II. 371Ч375
Means, one geometric mean between two square numbers, two between two cube numbers (Plato) II. 294 363Ч365
Means, three kinds, arithmetic, geometric and harmonic II. 292Ч293
Medial (straight line), an unlimited number of irrationals can be derived from medial straight line III. 254Ч255
Medial (straight line), connected by Theaetetus with geometric mean III. 3 4
Medial (straight line), defined III. 49 50
Medial (straight line), medial area III. 54Ч55
meguar = axis I. 93
Mehler, F.G. I. 404 III. 284Ч285
Meier, Rudolf I. 21n. III. 522
Menaechmus I. 117 125 133n.
Menaechmus on elements I. 114
Menaechmus, story of M. and Alexander I. 1
Menelaus I. 21 23
Menelaus, direct proof of I. 25 I. 300
Middle term, or cause, in geometry, illustrated by Eucl. III. 31 I. 149
Mill, J.S. I. 144
Minor (irrational) straight line, biquadratic of which it is root III. 7
Minor (irrational) straight line, defined III. 163Ч164
Minor (irrational) straight line, equivalent to square root of fourth apotome III. 203Ч206
Minor (irrational) straight line, uniquely formed III. 172Ч173
Mocenigo, Prince I. 97Ч98
Moderatus, a Pythagorean II. 280
Mollweide, C.B. I. 108
Mondore (Montaureus), Pierre I. 102
Moses b. Tibbon I. 76
Motion, in mathematics I. 226
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 )
) 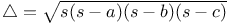

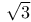
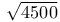 by means of sexagesimal fractions
by means of sexagesimal fractions