|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heath T.L. (ed.) Ч Thirteen Books of Euclid's Elements, Vol. 3 |
|
|
 |
| ѕредметный указатель |
Proportion, proportion in three terms (Aristotle makes it four) the "least" II. 131
Proportion, proportionals of vII. Def. 20 (numbers) a particular case of those of V. Def. 5 (Simson's Props. C, D and notes) II. 126Ч129 III.
Proportion, proportions enable any quadratic equation with real roots to be solved II. 187
Proportion, supposed use of propositions of Book V. in arithmetical Books II. 314 320
Proportion, three "proportions" II. 292
Proportion, three "proportions", but proportion par excellence or primary is continuous or geometric II. 292Ч293
Proportion, V. Def. 5 corresponds to Weierstrass' conception of number in general and to Dedekind's theory of irrationals II. 124Ч126
Proportion, X. 5 as connecting two theories II. 113
Proposition, formal divisions of I. 129Ч131
Protarchus I. 5 III.
Psellus, Michael, scholia by I. 70 71 II.
Pseudana of Euclid I. 7
Pseudana of Euclid, Pseudographemata I. 7n.
Pseudoboethius I. 92
Ptolemy I. I. 1 2
Ptolemy I., story of Euclid and Ptolemy I. 1
Ptolemy, Claudius I. 30n. II. 117 119 III.
Ptolemy, Claudius on Parallel-Postulate I. 28n. 34 43 45
Ptolemy, Claudius, attempt to prove it I. 204Ч206
Ptolemy, Claudius, Harmonica of, and commentary on I. 17
Ptolemy, Claudius, lemma about quadrilateral in circle (Simson's VI. Prop. D) II. 225Ч227
Pyramid, definitions of, by Euclid III. 261
Pyramid, definitions of, by others III. 268
Pyramidal numbers II. 290
Pyramidal numbers, pyramids truncated, twice-truncated etc. II. 291
Pythagoras I. 4n. 36
Pythagoras, construction of figure equal to one and similar to another rectilineal figure II. 254
Pythagoras, introduced "the most perfect proportion in four terms and specially called 'harmonic'" into Greece II. 112
Pythagoras, probable method of discovery of I. 47 and proof of I. 352Ч355
Pythagoras, rule for forming right-angled triangles in rational numbers I. 351 356Ч359 385
Pythagoras, story of sacrifice I. 37 343 350
Pythagoras, suggestions by Bretschneider and Hankel I. 354
Pythagoras, suggestions by Zeuthen I. 355Ч356
Pythagoras, supposed discoverer of application of areas I. 343Ч344 III.
Pythagoras, supposed discoverer of construction of five regular solids II. 97 III.
Pythagoras, supposed discoverer of the irrational I. 351 III. 524Ч525
Pythagoras, supposed discoverer of theorem of I. 47 I. 343Ч344 350Ч354 III.
Pythagoreans I. 19 36 155 188 279
Pythagoreans, "rational" and "irrational diameter of 5" I. 399Ч400 III.
Pythagoreans, 7/5 as approximation to 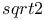 II. 119 II. 119
Pythagoreans, and of other regular solids III. 438 525
Pythagoreans, angles of triangle equal to two right angles, theorem and proof I. 317Ч320
Pythagoreans, approximation to 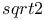 by "side-" and "diagonal-" numbers I. 398Ч400 III. 20 by "side-" and "diagonal-" numbers I. 398Ч400 III. 20
Pythagoreans, called 10 "perfect" II. 294
Pythagoreans, construction of dodecahedron in sphere II. 97
Pythagoreans, construction of isosceles triangle of Eucl. IV. 10, and of regular pentagon II. 97Ч98 III.
Pythagoreans, definitions of even and odd II. 281
Pythagoreans, definitions of unit II. 279
Pythagoreans, distinguished three sorts of means, arithmetic, geometric and harmonic II. 112
Pythagoreans, gnomon Pythagorean I. 351
Pythagoreans, had theory of proportion applicable to commensurables only II. 112
Pythagoreans, method of application of areas (including exceeding and falling-short) I. 343 384 403 II. 258Ч260 263Ч265 266Ч267
Pythagoreans, possible method of discovery of latter II. 97Ч99
Pythagoreans, proof of incommensurability of 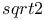 III. 2 III. 2
Pythagoreans, story of Pythagorean who, having divulged the irrational, perished by shipwreck III. 1
Pythagoreans, term for surface I. 169
Pythagoreans, three polygons which in contact fill space round point I. 318 II.
Q.E.D. (or F.) I. 57
Qadizade ar-Rumi I. 5n. 90
Quadratic equations, but method gives both roots if real II. 258
Quadratic equations, condition of possibility of solving equation of Eucl. VI. 28 II. 259
Quadratic equations, exact correspondence of geometrical to algebraical solution II. 263Ч264 266Ч267
Quadratic equations, geometrical solution of particular quadratics I. 383Ч385 386Ч388
Quadratic equations, indication that Greeks solved them numerically III. 43Ч44
Quadratic equations, one solution only given, for obvious reasons II. 260 264 267
Quadratic equations, solution assumed by Hippocrates I. 386Ч387
Quadratic equations, solution of general quadratic by means of proportions II. 187 263Ч265 266Ч267
Quadratrix I. 265Ч266 330
Quadrature definitions of I. 149
Quadrilateral, condition for inscribing circle in II. 93 95
Quadrilateral, inscribing in circle of quadrilateral equiangular to another II. 91Ч92
Quadrilateral, quadrilateral in circle, Ptolemy's lemma (Simson's VI. Prop. D) II. 225Ч227
Quadrilateral, quadrilateral not a "polygon" II. 239
Quadrilateral, varieties of I. 188Ч190
Quadrinomial (straight line), compound irrational (extension from binomial) III. 256
Quintilian I. 333
Qusta b. Luqa al-Ba'labakki, translator of "Books XIV, XV" I. 76 87 88
Radius, no Greek word for I. 199 II.
Ramus, Petrus (Pierre de la Ramee) I. 104
Ratdolt, Erhard I. 78 97
Ratio, "ratio compounded of their sides" (careless expression) II. 248
Ratio, alternate ratio, alternando II. 134
Ratio, arguments about greater and less ratios unsafe unless they go back to original definitions (Simson on V. 10) II. 156Ч157
Ratio, composition of ratio, componendo, different from compounding ratios II. 134Ч135
Ratio, compound ratio II. 132Ч133 189Ч190 234
Ratio, conversion of ratio, convertendo II. 135
Ratio, def. of greater ratio only one criterion (there are others) II. 130
Ratio, definition of II. 116Ч119
Ratio, definition of, Barrow's defence of it II. 117
Ratio, definition of, no sufficient ground for regarding it as spurious II. 117
Ratio, division of ratios used in Data as general method alternative to compounding II. 249Ч250
Ratio, duplicate, triplicate etc. ratio as distinct from double, triple etc. II. 133
Ratio, ex aequali in perturbed proportion II. 136
Ratio, inverse ratio, inversely II. 134
Ratio, means of expressing ratio of incommensurables is by approximation to any degree of accuracy II. 119
Ratio, method of transition from arithmetical to more general sense covering incommensurables II. 118
Ratio, names for particular arithmetical ratios II. 292
Ratio, operation of compounding ratios II. 234
Ratio, ratio ex aequali II. 136
Ratio, separation of ratio, separando (commonly dividendo) II. 135
Ratio, test for greater ratio easier to apply than that for equal ratio II. 129Ч130
Ratio, tests for greater, equal and less ratios mutually exclusive II. 130Ч131
Rational, "rational diameter of 5" I. 399Ч400
Rational, (of ratios) I. 137
Rational, any straight line may lie taken as rational and the irrational is irrational in relation thereto III. 10
Rational, rational right-angled triangles see "Right-angled triangles"
Rational, rational straight line is still rational if commensurable with rational straight line in square only (extension of meaning by Euclid) III. 10 11Ч12
Rationalisation of fractions with denominator of form 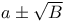 or or 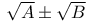 III. 243Ч252 III. 243Ч252
Rauchfuss see "Dasypodius"
Rausenberger, O. I. 157 175 313 III. 309
Reciprocal or reciprocally-related figures, definition spurious II. 189
Rectangle = rectangular parallelogram I. 370
Rectangle, "rectangle contained by" I. 370
Rectilineal angle, "rectilineal segment" I. 196
Rectilineal angle, definitions classified I. 179Ч181
Rectilineal angle, rectilineal figure I. 187
Reductio ad absurdum I. 134
Reductio ad absurdum, a variety of Analysis I. 140
Reductio ad absurdum, by exhaustion I. 285 293
Reductio ad absurdum, described by Aristotle and Proclus I. 136
Reductio ad absurdum, nominal avoidance of I. 369
Reductio ad absurdum, synonyms for, in Aristotle I. 136
Reductio ad absurdum, the only possible method of proving Eucl. III. 1 II. 8
Reduction, technical term, explained by Aristotle and Proclus I. 135
Reduction, technical term, explained by Aristotle and Proclus, first "reduction" of a difficult construction due to Hippocrates I. 135 II.
Regiomontanus (Johannes Mueller of Koenigsberg) I. 93 96 100
Reyher, Samuel I. 107
Rhaeticus I. 10 III.
Rhomboid I. 189
Rhombus, meaning and derivation I. 189
Riccardi, P. I. 96 112 202
Riemann, B. I. 219 273 274 280
Right angle, construction when drawn at extremity of second line (Heron) I. 270
Right angle, definition I. 181
Right angle, drawing straight line at right angles to another, Apollonius' construction for I. 270
Right-angled triangles, rational, connexion of rules with Eucl. II. 4, 8 I. 360
Right-angled triangles, rational, discovery of rules by means of gnomons I. 358Ч360
Right-angled triangles, rational, rational right-angled triangles in Apastamba I. 361 363
Right-angled triangles, rational, rule for finding, by Euclid 63Ч64
Right-angled triangles, rational, rule for finding, by Plato I. 356 357 359 360 385
Right-angled triangles, rational, rule for finding, by Pythagoras I. 356Ч359
Roeth I. 357Ч358
Rouche and de Comberousse I. 313
Rudd, Capt. Thos. I. 110
Ruellius, Joan. (Jean Ruel) I. 100
Russell, Bertrand I. 227 249
Sa'id b. Mas'ud b. al-Qass I. 90
Saccheri, Gerolamo I. 106 144Ч145 167Ч168 185Ч186 194 197Ч198 200Ч201 II. 130
Saccheri, Gerolamo, proof of existence of fourth proportional by Eucl. VI. 1, 2 and 12 II. 170
Sathapatha-Brahmana I. 362
| Savile, Henry I. 105 166 245 250 262 II.
Scalene I. 187Ч198
Scalene of cone (Apollonius) I. 188
Scalene of numbers (=odd) I. 188
Scalene, a class of solid numbers II. 290
Schessler, Chr. I. 107
Scheubel, Joan. I. 101 107
Schiaparelli, G.V. I. 163
Schluessel, Christoph see "Clavius"
Schmidt, Max C.P. I. 304 319
Schmidt, W., editor of Heron, on Heron's date I. 20Ч21
Scholia to Elements and MSS. of I. 64Ч74
Scholia to Elements and MSS. of, "Schol. Vat." partly derived from Pappus' commentary I. 66
Scholia to Elements and MSS. of, classes of, "Schol. Vat." I. 65Ч69
Scholia to Elements and MSS. of, classes of, "Schol. Vind." I. 69Ч70
Scholia to Elements and MSS. of, classes of, miscellaneous I. 71Ч74
Scholia to Elements and MSS. of, evidence in, as to text I. 64Ч65 66Ч67
Scholia to Elements and MSS. of, historical information in I. 64
Scholia to Elements and MSS. of, many from Geminus solely III. 522
Scholia to Elements and MSS. of, many scholia partly extracted from Proclus on Bk. I. I. 60 69 72
Scholia to Elements and MSS. of, numerical illustrations in, in Greek and Arabic numerals I. 71 III.
Scholia to Elements and MSS. of, scholia by Joannes Pediasimus I. 72Ч73
Scholia to Elements and MSS. of, scholia by Maximus Planudes I. 72
Scholia to Elements and MSS. of, scholia by Psellus I. 70Ч71
Scholia to Elements and MSS. of, scholia in Latin published by G. Valla, Commandinus, Conrad Dasypodius I. 73
Scholia to Elements and MSS. of, scholia on Eucl. II. 13 I. 407
Scholia to Elements and MSS. of, Scholium IV. No. 2 ascribes Book IV. to Pythagoreans II. 97 III.
Scholia to Elements and MSS. of, scholium published later by Heiberg attributes Scholium X. No. 62 to Proclus III. 521Ч522
Scholia to Elements and MSS. of, Scholium V. No. 1 attributes Book V. to Eudoxus II. 112
Scholia to Elements and MSS. of, Scholium X. No. 1 attributes discovery of irrational and incommensurable to Pythagoreans III. 1
Scholia to Elements and MSS. of, sometimes interpolated in text I. 67
Scholia to Elements and MSS. of, sources go back as far as Theodorus III. 522
Scholiast to Clouds of Aristophanes II. 99
Schopenhauer I. 227 354
Schotten, H. I. 167 174 179 192Ч193 202
Schultze, A. and Sevenoak, F.L. III. 284 303 331
Schumacher I. 321
Schur, F. I. 328
Schweikart, F.K. I. 219
Scipio Vegius I. 99
Sectio Canonis by Euclid I. 17 II. III.
Section = point of section I. 170 171 383
Section, "the section" see "Golden section"
Sector (of circle), explanation of name: two kinds (1) with vertex at centre, (2) with vertex at circumference II. 5
Sector-like (figure) II. 5
Sector-like (figure), bisection of such a figure by straight line II. 5
Seelhoff, P. III. 527
Segment of circle, angle of I. 253 II.
Segment of circle, segment less than semicircle I. 187
Segment of circle, similar segments II. 5
Semicircle I. 186
Semicircle, angle in semicircle a right angle, pre-Euclidean proof II. 63
Semicircle, angle of I. 182 253 II. 39Ч41 see
Semicircle, centre of I. 186
Separation of ratio and separando II. 135
Separation of ratio and separando, separando and componendo used relatively to one another, not to original ratio II. 168 170
Seqt I. 304
Serenus of Antinoeia I. 203
Serle, George I. 110
Servais, C. III. 527
Setting-out, one of formal divisions of a proposition I. 129
Setting-out, one of formal divisions of a proposition, may be omitted I. 130
Sexagesimal fractions in scholia III. 523
Sextus Empiricus I. 62 63 184
Shamsaddin as-Samarqandi I. 5n. 89
Sides of plane and solid numbers II. 287Ч288
Sigboto I. 94
Similar plane and solid numbers I. 357 II.
Similar plane and solid numbers, one mean between two similar plane numbers II. 294 371Ч272
Similar plane and solid numbers, two means between two similar solid numbers II. 294 373Ч375
Similar rectilineal figures, def. gives at once too little and too much II. 188
Similar rectilineal figures, def. of, given in Aristotle II. 188
Similar rectilineal figures, similar figures on straight lines which are proportional are themselves proportional and conversely (VI. 22), alternatives for proposition II. 242Ч247
Similar segments of circles II. 5
Similar solids, definitions of III. 261 265Ч267
Simon, Max I. 108 155 157Ч158 167 202 328 II. 134
Simplicius I. 22 167 171 184 185 197 203 223 224 III.
Simplicius on Eudemus' style I. 35 38
Simplicius on lunes of Hippocrates I. 29 35 386Ч387
Simplicius on parallels I. 190Ч191
Simplicius, commentary on Euclid I. 27Ч28
SIMPSON, THOMAS II. 121 III.
Simson, Robert I. 185 186 255 259 287 293 296 322 328 384 387 403 II. 3 8 22 23 33 34 37 43 49 53 70 73 79 90 117 131 132 140 143Ч144 145 146 148 154 161 162 163 165 170Ч172 177 179 180 182 183 184 185 186 189 193 195 209 211 212 230Ч231 238 252 269 270 272Ч273 III. 266 273Ч274 275 276 286Ч287 289 295 301 309 314 321 324 327 331 334 340 341 349 351 359 362 375 433 434
Simson, Robert on "vitiations" in Elements due to Theon I. 46 103 104 106 111 148
Simson, Robert on Euclid's Porisms I. 14
Simson, Robert, Axioms to Bk. V. II. 137
Simson, Robert, Bk. VI. Prop. A extending VI. 3 to case where external angle bisected II. 197
Simson, Robert, definition of plane I. 172Ч173
Simson, Robert, important note showing flaw in V. 10 and giving alternative II. 156Ч157
Simson, Robert, Prop. B (inversion) II. 144
Simson, Robert, Prop. D, Book XI. III. 345
Simson, Robert, Prop. E (convertendo) II. 175
Simson, Robert, Props. B, C, D II. 222Ч227
Simson, Robert, Props. C, D (Bk. V.) connecting proportionals of VII. Def. 20 as particular case with those of V. Def. 5 II. 126Ч129 III.
Simson, Robert, remarks on VI. 27-29 II. 258Ч259
Simson, Robert, shortens V. 8 by compressing two cases into one II. 152Ч153
Sind b. 'Ali Abu 't-Taiyib I. 86
Size, proper translation in V. Def. 3 II. 116Ч167 189Ч190
Smith and Bryant, alternative proofs of V. 16, 17, 18 by means of VI. 1 I. 404 III. 275 284 303 307
Smith and Bryant, alternative proofs of V. 16, 17, 18 by means of VI. 1, where magnitudes are straight lines or rectilineal areas II. 165Ч166 169 173Ч174
Solid angle, definitions of III. 261 267Ч268
Solid angle, solid "angle" of "quarter of sphere", of cone, or of half-cone III. 268
Solid numbers, three varieties according to relative lengths of sides II. 290Ч291
Solid, definition of III. 260 262Ч263
Solid, equal and similar solids III. 261 265Ч267
Solid, similar solids, definitions of III. 261 265Ч267
Speusippus I. 125
Sphaerica, early treatise on I. 17
Sphere, definitions of, by Euclid III. 261 269
Sphere, definitions of, by others III. 269
Spherical number, a particular species of cube number II. 291
Spiral of Archimedes I. 26 267
Spiral, "single-turn" I. 122Ч123n. 164Ч165
Spiral, "single-turn" in Pappus = cylindrical helix I. 165
Spire (tore) or Spiric surface I. 163 170
Spire (tore) or Spiric surface, varieties of I. 163
Spiric curves or sections, discovered by Perseus I. 161 162Ч164
Square number, product of equal numbers II. 289 291
Square number, product of equal numbers, one mean between square numbers II. 294 363Ч264
St Vincent, Gregory of I. 401 404
Steenstra, Pybo I. 109
Steiner, Jakob I. 193
Steinmann, Johann III. 523
Steinmetz, Moritz I. 101 III.
Steinschneider, M. I. 8n. 76sqq.
Stephanus Gracilis I. 101Ч102
Stephen Clericus I. 47
Stevin, Simon III. 8
Stifel, Michael III. 8
Stobaeus I. 3 II.
Stoic "axioms" I. 41 221
Stoic "axioms", illustrations I. 329
Stolz, O. I. 328 III.
Stone, E. I. 105
Straight line, Archimedes' assumption respecting I. 166
Straight line, division of straight line into any number of equal parts (an-Nairizi) I. 326
Straight line, Euclid's definition, interpreted by Proclus and Simplicius I. 166Ч167
Straight line, language and construction of I. 167
Straight line, language and construction of, and conjecture as to origin I. 168
Straight line, one or two cannot make a figure I. 169 183
Straight line, other definitions I. 168Ч169
Straight line, other definitions in Heron I. 168
Straight line, other definitions, by Legendre I. 169
Straight line, other definitions, by Leibniz I. 169
Straight line, pre-Euclidean (Platonic) definition I. 165Ч166
Straight line, straight line at right angles to plane, definition of III. 260
Straight line, straight line at right angles to plane, definition of, alternative constructions for III. 293Ч294
Straight line, two straight lines cannot enclose a space I. 195Ч196
Straight line, two straight lines cannot have a common segment I. 196Ч199 III.
Stroemer, Marten I. 113
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



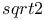
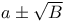 or
or