|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heath T.L. (ed.) — Thirteen Books of Euclid's Elements, Vol. 3 |
|
|
 |
| Предметный указатель |
Motion, in mathematics, motion without deformation considered by Helmholtz necessary to geometry I. 226—227
Motion, in mathematics, motion without deformation considered by Helmholtz necessary to geometry, but shown by Veronese to be petitio principii I. 226—227
Mueller, J.H.T. I. 189
Mueller, J.W. I. 365
Muh. b. 'Isa Abu 'Abdallah al-Mahani I. 85
Muh. b. Ahmad Abu 'r-Raihan al-Biruni I. 90
Muh. b. Ashraf Shamsaddin as-Samarqandi I. 89
Muhammad (b. 'Abdalbaqi) al-Bagdadi, translator of De divisionibus I. 8n. 90 110
Multinomial (straight line), an extension from binomial, probably investigated by Apollonius III. 256
Multiplication, definition of II. 287
Munich MS. of enunciations (R) I. 94—95
Musa b. Muh. b. Mahmud Qadizade ar-Rumi I. 5n. 90
Music, Elements of (Sectio Canonis), by Euclid I. 17 II.
Musici Scriptores Graeci II. 294
Napoleon I. 103
Nasiraddin at-Tusi I. 4 5n. 84 89 208—210 II.
Nazif b. Yumn (Yaman) al-Qass I. 76 77 87
Neide, J.G.C. I. 103
Nesselmann, G.H.F. II. 287 293 III. 526
Nicomachus I. 92 II. 119 131 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 300 363 III. 527
Nicomedes I. 42 160—161 265—266
Nipsus, Marcus Junius 1 305
Nixon, R.C.J. II. 16
Nominal and real definitions see "Definitions"
Number, defined by Thales, Eudoxus, Moderatus, Aristotle, Euclid II. 280
Number, Nicomachus and Iamblichus on II. 280
Number, represented by lines II. 287
Number, represented by lines and by points or dots II. 288—289
Objection, technical term, in geometry I. 135 257 260 265
Objection, technical term, in logic (Aristotle) I. 135
Oblong, (of geometrical figure) I. 151 188
Oblong, (of number) in Plato II. 288
Oblong, but these terms denote two distinct divisions of plane numbers in Nicomachus, Theon of Smyrna and Iamblichus II. 289—290
octahedron II. 98
Octahedron, definition of III. 262
Octahedron, discovery of, attributed to Theaetetus III. 438
Octahedron, problem of inscribing in sphere, Euclid's solution III. 474—477
Octahedron, problem of inscribing in sphere, Pappus' solution III. 477
Odd (number), def. of odd and even by one another unscientific (Aristotle) I. 148—149 II.
Odd (number), defs. of in Nicomachus II. 281
Odd (number), Nicom. and Iambl. distinguish three classes of odd numbers (1) prime and incomposite, (2) secondary and composite, as extremes, (3) secondary and composite in themselves but prime and incomposite to one another, which is intermediate II. 287
Odd (number), Pythagorean definition II. 281
Odd-times even (number), definition in Eucl. "spurious II. 283—284
Odd-times even (number), definition in Eucl. "spurious, and differs from definitions by Nicomachus etc. II. 283—284
Odd-times odd (number), defined in Eucl. but not in Nicom. and Iambl. II. 284
Odd-times odd (number), Theon of Smyrna applies term to prime numbers II. 284
Oenopides of Chios I. 34 36 126 271 295 371 III. 526
Ofterdinger, L.F. I. 9n. 10
Olympiodorus I. 29
Oppermann I. 151
Optics of Euclid I. 17
Oresme, N. I. 97
Orontius Finaeus (Oronce Fine) I. 101 104
Ozanam, Jaques I. 107 108
Paciuolo, Luca I. 98—99 100 III.
Pamphile I. 317 319
Pappus I. 17 39 133n. 137 151 225 388 391 401 II. 27 29 67 79 81 113 133 211 250 251 292 III.
Pappus on Analysis and Synthesis I. 138—139 141—142
Pappus on conchoids I. 161 266
Pappus on converse of Post. 4 I. 25 201
Pappus on Euclid's Data I. 8
Pappus on Euclid's Porisms I. 10—14
Pappus on Euclid's Surface-loci I. 15 16
Pappus on isoperimetric figures I. 26 27 333
Pappus on loci I. 329 330
Pappus on paradoxes of Erycinus I. 27 290
Pappus on quadratrix I. 266
Pappus on Treasury of Analysts I. 8 10 11 138
Pappus, additional axioms by I. 25 223 224 232
Pappus, assumes case of VI. 3 where external angle bisected (Simson's VI. Prop. A) II. 197
Pappus, commentary on Book X. survives in Arabic III. 3
Pappus, commentary on Elements I. 24—27
Pappus, commentary on Elements, partly preserved in scholia I. 66
Pappus, contrasts Euclid and Apollonius I. 3
Pappus, evidence of scholia as to Pappus' text I. 66—67
Pappus, extension of I. 47 I. 366
Pappus, lemma on Apollonius' Plane II. 64—65
Pappus, lemmas in Book X. interpolated from I. 67
Pappus, methods of inscribing regular solids in sphere, cube III. 480
Pappus, methods of inscribing regular solids in sphere, dodecahedron III. 501—503
Pappus, methods of inscribing regular solids in sphere, icosahedron III. 489—491
Pappus, methods of inscribing regular solids in sphere, octahedron III. 477
Pappus, methods of inscribing regular solids in sphere, tetrahedron III. 472—473
Pappus, problem from same work II. 81
Pappus, proof of I. 5 by I. 254
Pappus, quotations from it III. 3—4 255—259
Pappus, semi-algebraical methods in I. 373 378
Pappus, theorem from Apollonius' Plane Loci II. 198
Pappus, theorem that ratio compounded of ratios of sides (of equiangular parallelograms) is equal to ratio of rectangles contained by sides II. 250
Pappus, use of Euclid's irrationals III. 9 10
Papyrus, Herculanensis No. 1061 I. 50 184
Papyrus, Herculanensis No. 1061, Fayum I. 51 337 338
Papyrus, Herculanensis No. 1061, Oxyrhynchus I. 50
Papyrus, Herculanensis No. 1061, Rhind I. 304
Paradoxes, in geometry I. 188
Paradoxes, in geometry of Erycinus I. 27 290 329
Paradoxes, in geometry, an ancient "Budget of Paradoxes" I. 329
Parallelogram (=parallelogrammic area), first introduced I. 325
Parallelogram (=parallelogrammic area), first introduced, rectangular parallelogram I. 370
Parallels, Aristotle on I. 190 191—192
Parallels, as equi-distants I. 190—191 194
Parallels, definitions by "Aganis" I. 191
Parallels, definitions classified I. 192—194
Parallels, definitions, Geminus I. 191
Parallels, definitions, Posidonius I. 190
Parallels, definitions, Simplicius I. 190
Parallels, direction-theory of I. 191—192 194
Parallels, Legendre's attempt to establish theory of I. 213—219
Parallels, parallel planes, definition of III. 260 265
Parallels, Parallel Postulate see "Postulate 5"
Parallels, Veronese's definition and postulate I. 194
Paris MSS. of Elements, (p) I. 49
Paris MSS. of Elements, (q) I. 50
Pasch, M. I. 157 228 250
Pediasimus, Joannes I. 72—73
Peithon I. 203
Peletarius (Jacques Peletier) I. 103 104 249 407 II. 56 84 146 190
Peletarius (Jacques Peletier) on angle of contact and angle of semicircle II. 41
Pena I. 104
Pentagon, decomposition of regular pentagon into 30 elementary triangles II. 98
Pentagon, relation to pentagram II. 99
Pentagonal numbers II. 289
Perpendicular, "plane" and "solid" I. 272
Perpendicular, definition I. 181
Perpendicular, perpendicular and obliques I. 291
Perpendicular, perpendicular to plane III. 260 263
Perpendicular, perpendicular to two straight lines not in one plane III. 306—307
Perseus I. 42 162—163
Perturbed proportion II. 136 176—177
Petrus Montaureus (Pierre Mondore) I. 102
Peyrard and Vatican MS. 190 (P) I. 46 47 103 108
Pfleiderer, C.F. I. 168 298 II.
Phaenomena of Euclid I. 16 17
Philippus of Mende I. 1 116
Phillips, George I. 112
Philo of Byzantium I. 20 23
Philo of Byzantium, proof of I. 8 I. 263—264
Philolaus I. 34 351 371 399 II. III.
Philoponus I. 45 191—192 II. 282
Plane (or plane surface), "Simson's" definition ("axiom of the plane") I. 172—173 III.
Plane (or plane surface), "Simson's" definition ("axiom of the plane"), and Gauss on I. 172—173
Plane (or plane surface), Archimedes' assumption I. 171 172
Plane (or plane surface), Crelle's tract on I. 172—174
Plane (or plane surface), Enriques and Amaldi, Ingrami, Veronese and Hilbert on I. 175
Plane (or plane surface), evolution of, by Bolyai and Lobachewsky I. 174—175
Plane (or plane surface), other ancient definitions of, in Proclus, Heron, Theon of Smyrna, an-Nairizi I. 171—172
Plane (or plane surface), other definitions by Beez I. 176
Plane (or plane surface), other definitions by Deahna I. 174
Plane (or plane surface), other definitions by Fourier I. 173
Plane (or plane surface), other definitions by J.K. Becker I. 174
| Plane (or plane surface), other definitions by Leibniz I. 176
Plane (or plane surface), parallel planes defined III. 260 265
Plane (or plane surface), plane at right angles to plane, Euclid's definition of III. 260 263
Plane (or plane surface), plane at right angles to plane, Euclid's definition of, and alternative definition making it a particular case of "inclination" III. 303—304
Plane (or plane surface), Plato's definition of I. 171 III.
Plane (or plane surface), possible origin of Euclid's def. I. 171
Plane (or plane surface), Proclus' and Simplicius' interpretation of Euclid's def. I. 171
Plane numbers, product of two factors ("sides" or "length" and "breadth") II. 287—288
Plane numbers, product of two factors ("sides" or "length" and "breadth") in Plato either square or oblong II. 287—288
Plane numbers, product of two factors ("sides" or "length" and "breadth"), one mean proportional between similar plane numbers II. 371—372
Plane numbers, product of two factors ("sides" or "length" and "breadth"), similar plane numbers II. 293
Planudes, Maximus I. 72
Plato I. 1 2 3 137 155—156 159 184 187 203 221 III. 3
Plato, supposed invention of Analysis by I. 134
Plato, supposed invention of Analysis by on art of stereometry (length, breadth, and depth), next to geometry but commonly put after astronomy because little advanced III. 262
Plato, supposed invention of Analysis by on golden section II. 99
Plato, supposed invention of Analysis by on square and oblong numbers II. 288 290
Plato, supposed invention of Analysis by, "rational diameter of 5" I. 399
Plato, supposed invention of Analysis by, "rational diameter of 5", gives 7/5 as approximation to 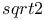 II. 119 II. 119
Plato, supposed invention of Analysis by, def. of plane surface I. 171
Plato, supposed invention of Analysis by, def. of straight line I. 165—166
Plato, supposed invention of Analysis by, generation of cosmic figures by putting together triangles I. 226 II. III. 525
Plato, supposed invention of Analysis by, passage of Theaetetus on square roots or surds II. 288 290 III. 524—525
Plato, supposed invention of Analysis by, rule for rational right-angled triangles I. 356 357 359 360 385
Plato, supposed invention of Analysis by, theorem that between square numbers one mean suffices, between cube numbers two means are necessary II. 294 364
Playfair, John I. 103 111
Playfair, John, "Playfair's" Axiom I. 220
Playfair, John, comparison of Axiom with Post. 5 I. 313—314 II.
Playfair, John, used to prove Eucl. I. 29 I. 312
Playfair, John, used to prove Eucl. I. 29, and Eucl. Post. 5 I. 313
Pliny I. 20 333
Plutarch I. 21 29 37 177 343 351 II. 254 III.
Point, an-Nairizi on I. 157
Point, attributes of, according to Aristotle I. 156
Point, interpretation of Euclid's definition I. 155
Point, is it sufficient? I. 156
Point, modem explanations by abstraction I. 157
Point, motion of, produces line I. 157
Point, negative character of Euclid's def. I. 156
Point, other definitions by "Herundes", Posidonius I. 156
Point, other definitions by Simplicius I. 157
Point, Plato's view of, and Aristotle's criticism I. 155—156
Point, Pythagorean definition of I. 155
Point, terms for I. 156
Polybius I. 331
Polygon, sum of exterior angles I. 322
Polygon, sum of interior angles (Proclus' proof) I. 322
Polygonal numbers II. 289
Polyhedral angles, extension of XI. 21 to III. 310—311
Porism, (1) = corollary I. 134 278—279
Porism, (2) as used in Porisms of Euclid, distinguished from theorems and problems I. 10 11
Porism, account of the Porisms given by Pappus I. 10—13
Porism, as corollary to proposition precedes "Q.E.D." or "Q.E.F." II. 8 64
Porism, interpolated Porisms (corollaries) I. 60—61 381
Porism, modern restorations by Simson and Chasles I. 14
Porism, Porism to IV. 15 mentioned by Proclus II. 109
Porism, Porism to VI. 19 II. 234
Porism, two senses I. 13
Porism, views of Heiberg I. 11 14
Porism, views of Heiberg, and of Zeuthen I. 15
Porphyry I. 17 136 277 283 287
Porphyry, commentary on Euclid I. 24
Porphyry, Symmikta I. 24 34 44
Poselger III. 8
Posidonius of Alexandria III. 521
Posidonius, the Stoic I. 20 21 27 28n. 189 197 III.
Posidonius, the Stoic on parallels I. 40 190
Posidonius, the Stoic, book directed against the Epicurean Zeno I. 34 43
Posidonius, the Stoic, definition of figure I. 41 183
Postulate 4, converse true only when angles rectilineal (Pappus) I. 201
Postulate 4, proofs of, resting on other postulates I. 200—201 231
Postulate 4, significance of I. 200
Postulate 5, attempts to prove, Lambert I. 212—213
Postulate 5, attempts to prove, Nasi-raddin at-Tusi I. 208—210
Postulate 5, attempts to prove, Proclus I. 206—208
Postulate 5, attempts to prove, Ptolemy I. 204—206
Postulate 5, attempts to prove, Saccheri I. 211—212
Postulate 5, attempts to prove, Wallis I. 210—211
Postulate 5, I. 30 is logical equivalent of I. 220
Postulate 5, Post. 5 proved from, and compared with, "Playfair's" Axiom I. 313—314
Postulate 5, probably due to Euclid himself I. 202
Postulate 5, Proclus on I. 202—203
Postulate 5, substitutes for, "Playfair's" axiom (in Proclus) I. 220
Postulate 5, substitutes for, Carnot, Laplace, Lorenz, W. Bolyai, Gauss, Worpitzky, Clairaut, Veronese, Ingrami I. 220
Postulate 5, substitutes for, Legendre I. 213 214 220
Postulate 5, substitutes for, others by Proclus I. 207 220
Postulate 5, substitutes for, Posidonius and Geminus I. 220
Postulate 5, substitutes for, Wallis I. 220
Postulate, distinguished from axiom, Euclid's view of, reconcileable with Aristotle's I. 119—120 124
Postulate, distinguished from axiom, famous "Postulate" or "Axiom of Archimedes" I. 234 III.
Postulate, distinguished from axiom, from hypothesis, by Aristotle I. 120—121
Postulate, distinguished from axiom, from hypothesis, by Proclus I. 121—122
Postulate, distinguished from axiom, Postulates 1, 2, significance of I. 195—196
Postulate, distinguished from axiom, postulates do not confine us to rule and compass I. 124
Postulate, distinguished from axiom, postulates in Archimedes I. 120 123
Postulate, distinguished from axiom, views of Heiberg, by Aristotle I. 118—119
Postulate, distinguished from axiom, views of Heiberg, by Proclus (Geminus and "others") I. 121—123
Potts, Robert I. 112 246
Prime (number), "prime and incomposite" II. 284
Prime (number), 2 admitted as prime by Eucl. and Aristotle, but excluded by Nicomachus, Theon of Smyrna and Iamblichus, who make prime a subdivision of odd II. 284—285
Prime (number), Aristotle on two senses of "prime" I. 146 II.
Prime (number), definitions of II. 284—285
Prime (number), definitions of "prime to one another" II. 285—286
Prime (number), different names for prime, "odd-times odd" (Theon), "linear" (Theon), "rectilinear" (Thymaridas), "euthymetrie" (Iamblichus) II. 285
Prime (number), prime absolutely or in themselves as distinct from prime to one another (Theon) II. 285
Principles, First I. 117—124
Prism, "parallelepipedal prisms" III. 404
Prism, definition of by Euclid III. 261
Prism, definition of by others III. 268—269
Problem, distinguished from theorem I. 124—128
Problem, distinguished from theorem in widest sense anything propounded (possible or not) but generally a construction which is possible I. 128—129
Problem, distinguished from theorem, another classification, (1) problem in excess, asking too much I. 129
Problem, distinguished from theorem, another classification, (2) deficient problem, giving too little I. 129
Problem, distinguished from theorem, problems classified according to number of solutions (a) one solution, ordered (b) a definite number, intermediate (c) an infinite number of solutions, unordered I. 128
Proclus II. 4 39 40 193 247 269 III. 10 264 267 273 310 441 524 525
Proclus on advantages of Euclid's Elements, and their object I. 115—116
Proclus on difficulties in three distinctions between postulates and axioms I. 123
Proclus on first principles, hypotheses, postulates, axioms I. 121—124
Proclus on formal divisions of proposition I. 129—131 II.
Proclus on the nature of elements and things elementary I. 114—116
Proclus on theorems and problems I. 124—129
Proclus on use of "quindecagon" for astronomy II. 111
Proclus, attempt to prove Postulate 5 I. 206—208
Proclus, books quoted by name in I. 34
Proclus, character of MS. used by I. 62 63
Proclus, commentary on Eucl. I, sources of I. 29—45
Proclus, commentary on Eucl. I, sources of, object and character of I. 31—32
Proclus, commentary on Plato's Republic, allusion in, to "side-" and "diagonal-" numbers in connexion with Eucl. II. 9, 10 I. 399—400
Proclus, commentary probably not continued, though continuation intended I. 32—33 III.
Proclus, details of career I. 29—30
Proclus, famous "summary" I. 37—38
Proclus, his own contributions I. 44—45
Proclus, list of writers quoted I. 44
Proclus, remarks on earlier commentators I. 19 33 45
Proof, necessary part of proposition I. 129—130
Proportion in giving older theory as well Euclid simply followed tradition II. 113
Proportion, "continuous" proportion II. 131 293
Proportion, "discrete" or "disjoined" II. 131 293
Proportion, "ordered" proportion, interpolated definition of II. 137
Proportion, "perturbed" proportion II. 136 176—177
Proportion, alternatives for v. Def. 5 by a geometer-friend of Saccheri, by Faifofer, Ingrami, Veronese, Enriques and Amaldi II. 126
Proportion, Aristotle on general proof (new in his time) of theorem (alternando) in proportion II. 113
Proportion, complete theory applicable to incommensurables as well as commensurables is due to Eudoxus I. 137 351 II.
Proportion, De Morgan on extension of meaning of ratio to cover incommensurables II. 118
Proportion, De Morgan's defence of V. Def. 5 as necessary and sufficient II. 122—124
Proportion, definition in V. Def. 5 substituted for that of VII. Def. 20 because latter found inadequate, not vice versa II. 121
Proportion, extensive use of proportions in Greek geometry II. 187
Proportion, interpolated definitions of proportion as "sameness" or "similarity of ratios" II. 119
Proportion, old (Pythagorean) theory practically represented by arithmetical theory of Eucl. VII. II. 113
Proportion, power of expressing incommensurable ratio is power of approximation without limit II. 119
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте