|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heath T.L. (ed.) — Thirteen Books of Euclid's Elements, Vol. 1 |
|
|
 |
| Предметный указатель |
Caiani, Angelo 101
Camerarius, Joachim 101
Camerer, J. G. 103 293
Camorano, Rodrigo 112
Campanus, Johannes 3 78 94—96 104 106 110 407
Candalla, Franciscus Flussates (Francois de Foix, Comte de Candale) 3 104 110
Cantor, Moritz 7n. 20 272 304 318 320 333 352 355 357—358 360 401
Carduchi, L. 112
Carpus, on Astronomy 34 43 45 127 128 177
Case, technical term 134
Cases interpolated 58 59
Casiri 4n. 9n.
Cassiodorius, Magnus Aurelius 92
Cataldi, Pietro Antonio 106
Catoptrica, "Cause" consideration of, omitted by commentators 19 45
Catoptrica, attributed to Euclid, probably Theon's 17
Catoptrica, Catoptrica of Heron 21 253
Catoptrica, cause = middle term (Aristotle) 149
Catoptrica, definition should state cause (Aristotle) 149
Catoptrica, question whether geometry should investigate cause (Geminus) 45 150n.
Censorinus 91
Centre,  184—185 184—185
Ceria Aristotelica 35
Chasles on Porisms of Euclid 10 11 14 15
Chinese, "Tcheou pei" 355
Chinese, knowledge of triangle 3 4 5 352
Chrysippus 330
Cicero 91 351
Circle =  (Aristotle) 184 (Aristotle) 184
Circle = round,  (Plato) 184 (Plato) 184
Circle, a plane figure 183—184
Circle, bisected by diameter (Thales) 185 184—185
Circle, centre of 184—185
Circle, definition of 183—185
Circle, intersections with another circle 238—240 242—243 293—294
Circle, intersections with straight linei 237—238 272—274
Circle, pole of 185
Circumference,  184 184
Cissoid 161 164 176 330
Clairaut 328
Clavius (Christoph Schliissel) 103 105 194 232 381 $91 407
Claymundus, Joan. 101
Cleonides, Introduction to Harmony 17
Cochlias or cochlion (cylindrical helix) 162
Codex Leidensis 399
Codex Leidensis, I 22 27n. 79n.
Coets, Hendrik 109
Commandinus 4 102 103 104—105 106 110 111 407
Commandinus, edited (with Dee) De divisionibus 8 9 110
Commandinus, scholia included in translation of Elements 73
Commentators on Eucl. criticised by Proclus 19 26 45
Common Notions, = axioms 62 120—121 221—222
Common Notions, called "axioms" by Proclus 221
Common Notions, meaning and appropriation of term 221
Common Notions, which are genuine? 22—23 sq.
Complement,  "about diameter" 341 "about diameter" 341
Complement,  meaning of 341 meaning of 341
Complement,  not necessarily parallelograms 341 not necessarily parallelograms 341
Complement,  use for application of areas 342—343 use for application of areas 342—343
Composite, ativderos, (of lines) 160
Composite, ativderos, (of surfaces) 170
Conchoids 160—161 265—266 330
Conclusion, 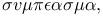 definition merely stating conclusion 149 definition merely stating conclusion 149
Conclusion, 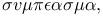 necessary part of a proposition 129—130 necessary part of a proposition 129—130
Conclusion, 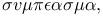 particular conclusion immediately made general 131 particular conclusion immediately made general 131
Congruence theorems for triangles, recapitulation of 305—306
Congruence-Axioms or Postulates, Common Notion 4 in 129—130
Congruence-Axioms or Postulates, modern systems of (Pasch, Veronese, Hilbert) 228—231
Conics, focus-directrix property proved by Pappus 15
Conics, fundamental property as proved by Apollonius equivalent to Cartesian equation 344—345
Conics, of Apollonius 3 16
Conics, of Aristaeus 3 16
Conies, of Euclid 3 16
Constantinus Lascaris 3
Construct 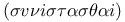 contrasted with apply to 343 contrasted with apply to 343
Construct 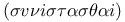 contrasted with describe on 348 contrasted with describe on 348
Construct 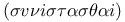 special connotation 259 289 special connotation 259 289
Construction,  , one of formal divisions of a proposition 129 , one of formal divisions of a proposition 129
Construction, mechanical 151 387
Construction, sometimes unnecessary 130
Construction, turns nominal into real definition 146
Continuity, principle of 234 sq. 242 272 294
Conversion, geometrical, "leading" and partial varieties 256—257 337
Conversion, geometrical, distinct from logical 256
Copernicus 101
Cordonis, Mattheus 97
Cratistus 133
Crelle, on the plane 172—174
Ctesibius 20 21 39n.
Cunn, Samuel 111
Curtze, Maximilian, editor of an-NairizI 22 78 92 94 96 97n.
Curves, classification of see “Line”
Cylindrical helix 161 162 329 330
Czecha, Jo. 113
Dasypodius (Rauchfuss), Conrad 73 102
Data of Euclid 8 132 141 385 391
De levi et ponderoso, tract 18
De Morgan 246 260 269 284 291 298 300 309 313 314 315 369 376
De Zolt 328
Deahna 174
Dechales, Claude Francois Milliet 106 107 108 110
Dedekind's Postulate, and applications 235—240
Dee, discovered De divisionibus 8 9
Dee, John 109 110
Definition, in sense of "closer statement"  , one of formal divisions of a proposition 129 , one of formal divisions of a proposition 129
Definition, may be unnecessary 130
Definitions, a class of thesis (Aristotle) 120
Definitions, Aristotle on 117 119 120 143
Definitions, Aristotle on unscientific definitions 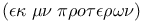 148—149 148—149
Definitions, Aristotle's requirements in 146—150
Definitions, but confused therewith by Proclus 121—122
Definitions, but say nothing about existence (except in the case of a few primary things) 119 143
Definitions, definitions of technical terms in Aristotle and Heron, not in Euclid 150
Definitions, distinguished from hypotheses 119
Definitions, Euclid's definitions agree generally with Aristotle's doctrine 146
Definitions, exceptions 148
Definitions, interpolated definitions 61 62
Definitions, must be assumed 117—119
Definitions, real and nominal definitions (real = nominal plus postulate or proof), Mill anticipated by Aristotle, Saccheri and Leibniz 143—145
Definitions, should state cause or middle term and be genetic 149—150
Definitions, terms for,  and and  143 143
Demetrius Cydonius 72
Democritus 38
Desargues 193
Describe on 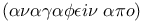 contrasted with construct 348 contrasted with construct 348
Diagonal 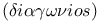 185 185
Diameter  , "rational" and "irrational" diameter of 5 , "rational" and "irrational" diameter of 5
Diameter  , (Plato) 399 , (Plato) 399
Diameter  , as applied to figures generally 325 , as applied to figures generally 325
Diameter  , of circle or parallelogram 185 , of circle or parallelogram 185
Diameter  , taken from Pythagoreans 399—400 , taken from Pythagoreans 399—400
Dimensions  157 158 157 158
Dimensions  , Aristotle's view of 158—159 , Aristotle's view of 158—159
Dinostratus 117 266
Diodes 164
Diodorus 203
Diogenes Laertius 37 305 317 351
Diophantus 86
Diorismus  (b) condition of possibility 128 (b) condition of possibility 128
Diorismus  = (a) "definition" or "specification, " a formal division of a proposition 129 = (a) "definition" or "specification, " a formal division of a proposition 129
Diorismus  determines how far solution possible and in how many ways 130—131 243 determines how far solution possible and in how many ways 130—131 243
Diorismus  diorismi said to have been discovered by Leon 116 diorismi said to have been discovered by Leon 116
Diorismus  first instances in elements 234 293 first instances in elements 234 293
Diorismus  introduced by introduced by  293 293
Diorismus  revealed by analysis 142 revealed by analysis 142
Dippe 108
Direction, as primary notion, discussed 179
Direction, direction-theory of parallels 191—192
Distance,  = radius 199 = radius 199
Distance,  in Aristotle has usual general sense and = dimension 199 in Aristotle has usual general sense and = dimension 199
| Division (method of), Plato's 134
Divisions (of figures) by Euclid 8 9
Divisions (of figures) by Euclid and (by Dee) in Latin translation 8 9 110
Divisions (of figures) by Euclid found (by Woepcke) in Arabic 9
Divisions (of figures) by Euclid translated by Muhammad al-Bagdadi 8
Dodgson, C.L. 194 254 261 313
Dou, Jan Pieterszoon 108
Duhamel. 139 328
Egyptians, knowledge of right-angled triangles 352
Elements, Arabian versions compared with Greek text 79—83
Elements, Arabian versions compared with one another 83 84
Elements, Arabic translations (1) by al-Hajjaj 75 76 79 80 83—84
Elements, Arabic translations (2) by Ishaq and Thabit b. Qurra 75—80 83—84
Elements, Arabic translations (3) Naslraddin at-Tusi 77—80 84
Elements, August's 103
Elements, Campanus 94—96 97—100
Elements, Campanus etc., Zamberti 98—100
Elements, Commandinus 104—105
Elements, contributions to, by Eudoxus 1 37
Elements, contributions to, Theaetetus 1 37
Elements, Euclid's Elements, commentators on 19—45
Elements, Euclid's Elements, ultimate aims of 2 115—116
Elements, external sources throwing light on text, Heron, Taurus, Sextus Empiricus, Proclus, Iamblichus 62—63
Elements, first principles of, definitions, postulates, common notions (axioms) 117—124
Elements, Gherard of Cremona 93—94
Elements, Greek texts, editio princeps 100—101
Elements, Gregory's 102—103
Elements, Hebrew translation by Moses b. Tibbon or Jakob b. Machir 76
Elements, Heiberg's passim translations and editions generally 97—113
Elements, Hermotimus of Colophon 117
Elements, immediate recognition of 116
Elements, interpolations before Theon's time 58—63
Elements, introduction into England 10th c 95
Elements, means of comparing Tfreonine with ante-Theonine text 51—53
Elements, no definitions of such technical terms 150
Elements, old translation of 10th c. 92
Elements, on the nature of elements (Aristotle) 116
Elements, on the nature of elements (Menaechmus) 114
Elements, on the nature of elements (Proclus) 114—116
Elements, Peyrard's 103
Elements, pre-Euclidean Elements, by Hippocrates of Chios, Leon 116
Elements, pre-Euclidean Elements, Theudius 117
Elements, Proclus 19 29—45
Elements, Proclus and passim, Aenaeas (Aigeias) 28
Elements, Proclus and passim, Aenaeas (Aigeias) mss. of 46—51
Elements, Proclus and passim, an-Nairlzi 21—24
Elements, Proclus and passim, Heron 20—24
Elements, Proclus and passim, Pappus 24—27
Elements, Proclus and passim, Porphyry 24
Elements, Proclus and passim, Simplicius 28
Elements, Proclus on advantages of Euclid's Elements 115
Elements, scholia 64—74
Elements, sections of Book I. 308
Elements, technical terms in connexion with 125—142
Elements, Theon's changes in text 54—58
Elements, translation by Athelhard 93—96
Elements, translation by Billingsley 109—110
Elements, translation by Boethius 92
Elinuam 95
Engel and Staeckel 219 321
Enriques, F. 157 175 193 195 201 313
Enunciation  , one of formal divisions of a proposition 129—130 , one of formal divisions of a proposition 129—130
Epicureans, objection to I. 20 41 287
Epicureans, Savile on 287
Equality, in sense different from that of congruence (= "equivalent," Legendre) 327—328
Equality, modern definition of 228
Equality, two senses of equal (1), "divisiblyequal" (Hilbert), or "equivalent by sum" (Amaldi), (2), "equal in content" (Hilbert), or "equivalent by difference" (Amaldi) 328
Eratosthenes I 162
Eratosthenes I, contemporary with Archimedes 1 2
Errard, Jean, de Bar-le-Duc 108
Erycinus 27 290 329
Euclid, "of Tus" 4 5n.
Euclid, "of Tyre" 4—6
Euclid, account of, in Proclus' summary I date 1—2
Euclid, allusions to in Archimedes I (according to Proclus) a Platonist 2
Euclid, Arabian derivation of name (" key of geometry") 6
Euclid, Arabian list of works 17 18
Euclid, Arabian traditions about 4 5
Euclid, bibliography 91—113
Euclid, Data 8 132 141 385 391
Euclid, Elements of Music or Sectio Canonis 17
Euclid, Elements, ultimate aim of 2 115—116
Euclid, not "of Megara" 3 4
Euclid, on "three- and four-line locus" 3
Euclid, On divisions (of figures) 8 9
Euclid, Optics 17
Euclid, other works, Conies 16
Euclid, Pappus on personality of 3
Euclid, Phaenomena 16 17
Euclid, Porisms 10—15
Euclid, Pseudaria 7
Euclid, story of (in Stobaeus) 3
Euclid, supposed to have been born at Gela 4
Euclid, Surface-loci 15 16
Euclid, taught at Alexandria 2
Eudemus 29
Eudemus, History of Geometry 34 35—38 278 295 304 317 320 387
Eudemus, On the Angle 34 38 177—178
Eudoxus 1 37 116
Eudoxus, discoverer of theory of proportion as expounded generally in Bks. v., VI. 137 351
Eudoxus, founder of method of exhaustion 234
Eudoxus, inventor of a certain curve, the hippopede, horse-fetter 163
Eudoxus, on the golden section 137
Eudoxus, possibly wrote Sphaerica 17
Euler, Leonhard 401
Eutocius 25 35 39 142 161 164 259 317 329 330 373
Exterior and interior (of angles) 263 280
Extremity,  182 183 182 183
Falk, H. 113
Figure, according to Posidonius is confining boundary only 41 183
Figure, angle-less 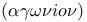 figure 187 figure 187
Figure, as viewed by Aristotle 182—183
Figure, as viewed by Euclid 183
Figure, as viewed by Plato 182
Figure, figures bounded by two lines classified 187
Figures, printing of 97
Fihrist 4n. 5n. 17 21 24 25 27
Fihrist, list of Euclid's works in 17 18
Finaeus, Orontius (Oronce Fine) 101 104
Flauti, Vincenzo 107
Florence MS. Laurent, XXVIII. 3, (F) 47
Flussates see “Candalla”
Forcadel, Pierre 108
FOURIER 173—174
Frankland, W.B. 173 199
Frischauf 174
Gartz 9n.
Gauss 172 193 194 202 219 321
Geminus, classification of angles 178—179
Geminus, classification of surfaces 170
Geminus, comm. on Posidonius 39
Geminus, elements of astronomy 38
Geminus, name not Latin 38—39
Geminus, on "mixed" lines (curves) and surfaces 162
Geminus, on homoeomeric (uniform) lines 162
Geminus, on parallels 191
Geminus, on Postulate 4 200
Geminus, on postulates and axioms 122—123
Geminus, on stages of proof of theorem of I. 32 317—321 27—28 37 44 45 133n 203 265 330
Geminus, on theorems and problems 128
Geminus, Proclus' obligations to 39—42
Geminus, title of work  quoted from by Proclus 39 quoted from by Proclus 39
Geminus, two classifications of lines (or curves) 160—162
Geometrical algebra 372—374
Geometrical algebra, Euclid's method in Book 11. evidently the classical method 373
Geometrical algebra, preferable to semi-algebraical method 377—378
Gherard of Cremona, translator of an-Nairizi's commentary 22 94
Gherard of Cremona, translator of Elements 93—94
Gherard of Cremona, translator of tract De divisionibus 9
Giordano, Vitale 106 176
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




 (Aristotle)
(Aristotle)  (Plato)
(Plato) 
 "about diameter"
"about diameter" 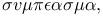 definition merely stating conclusion
definition merely stating conclusion 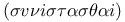 contrasted with apply to
contrasted with apply to  , one of formal divisions of a proposition
, one of formal divisions of a proposition  , one of formal divisions of a proposition
, one of formal divisions of a proposition 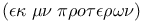
 and
and 
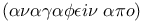 contrasted with construct
contrasted with construct 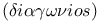
 , "rational" and "irrational" diameter of
, "rational" and "irrational" diameter of 
 (b) condition of possibility
(b) condition of possibility 
 = radius
= radius  , one of formal divisions of a proposition
, one of formal divisions of a proposition 
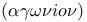 figure
figure  quoted from by Proclus
quoted from by Proclus