|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heath T.L. (ed.) — Thirteen Books of Euclid's Elements, Vol. 1 |
|
|
 |
| Предметный указатель |
Given,  , different senses 132—133 , different senses 132—133
Gnomon, (2) carpenter's square for drawing right angles 371
Gnomon, (3) figure placed round square to make larger square 351 371
Gnomon, (4) use extended by Euclid to parallelograms 371
Gnomon, (5) by Heron and Theon to any figures 371—372
Gnomon, arithmetical use of 358—360 371
Gnomon, Euclid's method of denoting in figure 383
Gnomon, Indian use of gnomon in this sense 362
Gnomon, introduced into Greece by Anaximander 370
Gnomon, literally "that enabling (something) to be known" 64 370
Gnomon, successive senses of, (1) upright marker of sundial 181 185 271—272
Gorland, A. 233 234
Gow, James 135n.
Gracilis, Stephanus 101—102
Grandi, Guido 107
Gregory of St Vincent 401 404
Gregory, David 102—103
Gromatici 91n. 95
Grynaeus 100—101
Halifax, William 108 110
Halliwell 95n.
Hankel, H. 139 144 232 234 344 354
Harmonica of Ptolemy, Comm. on 17
Harmony, Introduction to, not by Euclid 17
Harun ar-Rashid 75
Hauff, J.K.F. 108
Helix, cylindrical 161 162 329 330
Helmholtz 226 227
Henrici and Treutlein 313 404
Henrion, Denis 108
Herigone, Pierre 108
Herlin, Christian 100
Hermotimus of Colophon 1
Herodotus 37n. 370
Heron of Alexandria 137n. 159 163 168 170 171—172 176 183 184 185 188 189 222 223 243 253 285 287 299 351 369 371 405 407 408
Heron of Alexandria, addition to I. 47 366—368
Heron of Alexandria, apparently originated semi-algebraical method of proving theorems of Book II. 373 378
Heron of Alexandria, commentary on Euclid's Elements 20—24
Heron of Alexandria, comparison of areas of triangles in I. 24 334—335
Heron of Alexandria, direct proof of I. 25 301
Heron of Alexandria, Heron and Vitruvius 20—21
Heron of Alexandria, mechanicus, date of 20—21
Heron, Proclus' instructor 29
Hieronymus of Rhodes 305
hilbert 157 193 201 228—231 249 313 328
Hipparchus 4n. 30n.
Hippias of Elis 42 265—266
Hippocrates of Chios 8n. 29 35 38 116 135 136 386—387
Hippopede  , a certain curve used by Eudoxus 162—163 176 , a certain curve used by Eudoxus 162—163 176
Hoffmann, Heinrich 107
Hoffmann, John Jos. Ign. 108 365
Holiel, J. 219
Holtzmann, Wilhelm (Xylander) 107
Homoeomeric (uniform) lines 40 161 162
Hoppe, E. 21
Hornlike (angle),  177 178 182 265 177 178 182 265
Horsley, Samuel 106
Hudson, John 102
Hultsch, F. 20 329 400
Hunain b. Ishaq al-'Ibadi 75
Hypotheses, confused by Proclus with definitions 121—122
Hypotheses, geometer's hypotheses not false (Aristotle) 119
Hypotheses, in Aristotle 118—120
Hypotheses, in Plato 122
Hypothetical construction 199
Hypsicles 5
Iamblichus 63 83
Ibn al-'Amld 86
Ibn al-Haitham 88 89
Ibn al-Lubudi 90
Ibn Rahawaihi al-Arjani 86
Ibn Sina (Avicenna) 77 89
Incomposite (of lines) 160—161 (ofsurfaces)i7o
Indivisible lines  , theory of, rebutted 268 , theory of, rebutted 268
Infinite, Aristotle on the 232—234
Infinite, infinite division not assumed, but proved, by geometers 268
Infinity, parallels meeting at 192—193
Ingrami, G. 175 193 195 201 227—228
Interior and exterior (of angles) 263 280
Interior and opposite angle 280
Interpolations by Theon 46 55—56
Interpolations I. 40
Interpolations in the Elements before Theon's time 58—63
Interpolations interpolated 338
Irrational, "irrational diameter of 5", (Pythagoreans, and, Plato) 399—400
Irrational, approximation to  by means of "side-" and " diagonal-" numbers 399—401 by means of "side-" and " diagonal-" numbers 399—401
Irrational, claim of India to priority of discovery 363—364
Irrational, discovered with reference to  351 351
Irrational, Indian approximation to  361 363—364 361 363—364
Irrational, irrational ratio  137 137
Irrational, unordered irrationals (Apollonius) 42 115
Isaacus Monachus (or Argyrus) 73—74 407
Ishaq b. Hunain b. Ishaq al- Ibadi, Abu Yaqub, translation of Elements by 75—80 83—84
Ismail b. Bulbul 88
Isoperimetric (or isometric), figures, Pappus and Zenodorus on 26 27 333
Isosceles  187 187
Isosceles  of numbers (=even) 188 of numbers (=even) 188
Isosceles  isosceles right-angled triangle 352 isosceles right-angled triangle 352
Jakob b. Machir 76
Joannes Pediasimus 72—73
Junge, G., and discovery of irrationals to Pythagoras 351
Junge, G., on attribution of theorem of I. 47
Kaestner, A.G. 78 97 101
Katyayana Sulba — Sutra 360
Keill, John 105 110—121
Kepler 193
Killing, W. 194 219 225—226 235 242 272
Klamroth, M. 75—84
Kliigel, G.S. 212
Knesa, Jakob 112
Knoche 32n. 33n. 73
Kroll, W. 399—400
Lambert, J.H. 212—213
Lardner, Dionysius 112 246 250 298 404
Lascaris, Constantinus 3
Leading theorems (as distinct from converse) 257
Leading theorems (as distinct from converse) leading variety of conversion 256—257
Leeke, John 110
Lefevre, Jacques 100
Legendre, Adrien Marie 112 169 215—219
Leibniz 145 169 176 194
Leiden MS. 399
Leiden MS. I of al-Hajjaj and an-Nairizi 22
Lemma 114
Lemma, especially from Pappus 67
Lemma, lemmas interpolated 59—60
Lemma, meaning 133—134
Leodamas of Thasos 36 134
Leon 116
Limdgren, F.A.A. 113
Linderup, H.C. 113
Line, "asymptotic" or non-secant 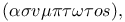 secant secant  161 161
Line, "divisible or continuous one way" (Aristotle) 158—159
Line, "flux of point" 159
Line, "magnitude extended one way" (Aristotle, "Heromides") 158
Line, Apollonius on 159
Line, classification of lines, Heron 159—160
Line, classification of lines, Plato and Aristotle 159—160
Line, composite  , incomposite , incomposite  "forming a figure" "forming a figure"  , determinate , determinate  , indeterminate , indeterminate  160 160
Line, Geminus, first classification 160—161
Line, Geminus, second classification 161
Line, homoeomeric (uniform) 161—162
Line, loci on lines 329 330
Line, objection of Aristotle 158
Line, Platonic definition 158
Line, Proclus on lines without extremities 165
Line, simple, "mixed" 161—162
Line, straight 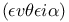 , curved , curved  , circular , circular 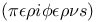 , spiral-shaped , spiral-shaped  bent bent  , broken , broken  , round , round 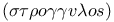 159 159
Linear, loci 330
Linear, problems 330
| Lionardo da Vinci, proof of I. 47 365—366
Lippert 88n.
Lobachewsky, N.I. 174—175 213 219
Locus-theorems  and loci and loci  as an area which is locus of area (parallelogram or triangle) 330 as an area which is locus of area (parallelogram or triangle) 330
Locus-theorems  and loci and loci  corresponding distinction between plane and solid problems, to which Pappus adds linear problems 330 corresponding distinction between plane and solid problems, to which Pappus adds linear problems 330
Locus-theorems  and loci and loci  further distinction in Pappus between (1), further distinction in Pappus between (1),  (2), (2),  (3), (3),  330 330
Locus-theorems  and loci and loci  loci likened by Chrysippus to Platonic ideas 330—331 loci likened by Chrysippus to Platonic ideas 330—331
Locus-theorems  and loci and loci  locus defined by Proclus 329 locus defined by Proclus 329
Locus-theorems  and loci and loci  locus-theorems and loci (1) on lines (a) plane loci (straight lines and circles) (b) solid loci (conies), (2) on surfaces 329 locus-theorems and loci (1) on lines (a) plane loci (straight lines and circles) (b) solid loci (conies), (2) on surfaces 329
Locus-theorems  and loci and loci  Proclus regards locus in I. 35 Proclus regards locus in I. 35
Locus-theorems  and loci and loci  Proclus regards locus in III. 21 31 Proclus regards locus in III. 21 31
Logical conversion, distinct from geometrical 256
Logical deductions 256 284—285 300
Logical deductions, logical equivalents 309 314—315
Lore 163
Lorenz, J.F. 107—108
Loria, Gino 7n. 10n. 11n. 12n.
Luca Paciuolo 98—99 100
Machir, Jakob b. 76
Magni, Domenico 106
Magnitude, common definition vicious 148
Mansion, P. 219
Manuscripts of Elements 46—51
Martianus Capella 91 155
Martin, T.H. 20 29n. 30n.
Mas'ud b. al-Qass al-Bagdadi 90
Maximus Planudes, scholia and lectures on Elements 72
meguar = axis 93
Mehler, F.G. 404
Meier, Rudolf 21n.
Menaechmus story of M. and Alexander I on elements 114 117 125 133n.
Menelaus 21 23
Menelaus, direct proof of I. 25 300
Middle term, or cause, in geometry, illustrated by III. 31 149
Miisa b. Muh. b. Mahmud Qadizade ar-Rumi 5n. 90
Mill, J.S. 144
Mocenigo, Prince 97—98
Mollweide, C.B. 108
Mondore (Montaureus), Pierre 102
Moses b. Tibbon 76
Motion, in mathematics 226
Motion, in mathematics, but shown by Veronese to be petitio principii 226—227
Motion, in mathematics, motion without deformation considered by Helmholtz necessary to geometry 226—227
Mueller, J.W. 365
Muh. b. 'Isa Abu 'Abdallah al-Mahani 85
Muh. b. Ahmad Abu 'r-Raihan al-Biruni 90
Muh. b. Ashraf Shamsaddin as-Samarqandi 89
Muhammad (b. 'Abdalbaqi) al-Bagdadi, translator of De divisionibus 8n. 90 110
Muller, J.H.T. 189
Munich MS. of enunciations (R) 94—95
Musici Elements of (Sectio Canonis)y by Euclid 17
Napoleon 103
Nasiraddin at-Tusi 4 5n. 77 84 89 208—210
Nazif b. Yumn (Yaman) al-Qass 76 77 87
Neide, J.G.C. 103
Nicomachus 92
Nicomedes 42 160—161 265—266
Nipsus, Marcus Junius 305
Nominal and real definitions see “Definitions”
Objection  , in logic (Aristotle) 135 , in logic (Aristotle) 135
Objection  , technical term, in geometry 135 257 260 265 , technical term, in geometry 135 257 260 265
Oblong 151 188
Oenopides of Chios 34 36 126 271 295 371
Ofterdinger, L.F. 9n. 10
Olympiodorus 29
Oppermann 151
Optics of Euclid 17
Oresme, N. 97
Orontius Finaeus (Oronce Fine) 101 104
Ozanam, Jaques 107 108
Paciuolo, Luca 98—99 100
Pamphile 317 319
Pappus 17 39 133n. 137 151 225 388 391 401
Pappus, additional axioms by 25 223 224 232
Pappus, commentary on Elements 24—27
Pappus, contrasts Euclid and Apollonius 3
Pappus, Data 8
Pappus, evidence of scholia as to Pappus' text 66—67
Pappus, extension of I. 47 366
Pappus, lemmas in Book X. interpolated from 67
Pappus, on Analysis and Synthesis 138—139 141—142
Pappus, on conchoids 161 266
Pappus, on converse of Post. 4 25 201
Pappus, on Euclid's Porisms 10—14
Pappus, on foci 329 330
Pappus, on isoperimetric figures 26 27 333
Pappus, on paradoxes of Erycinus 27 290
Pappus, on quadratrix 266
Pappus, on Treasury of Analysis 8 10 11 138
Pappus, partly preserved in scholia 66
Pappus, proof of I. 5 by 254
Pappus, semi-algebraical methods in 373 378
Pappus, Surface-loci 15 16
Papyrus, Fayum 51 337 338
Papyrus, Herculanensis No. 1061 50 184
Papyrus, Oxyrhynchus 50
Papyrus, Rhind 304
Paradoxes, an ancient "Budget of Paradoxes" 329
Paradoxes, in geometry 188
Paradoxes, of Erycinus 27 290 329
Parallelogram (= parallelogrammic area), first introduced 325
Parallelogram (= parallelogrammic area), rectangular parallelogram 370
Parallels, Aristotle on 190 191—192
Parallels, as equidistants 190—191 194
Parallels, definitions classified 192—194
Parallels, definitions, by "Aganis" 191
Parallels, definitions, by Geminus 191
Parallels, direction-theory of 191—192 194
Parallels, Legendre's attempt to establish theory of 213—219
Parallels, Parallel Postulate see “Postulate 5”
Parallels, Posidonius 190
Parallels, Simplicius 190
Parallels, Veronese's definition and postulate 194
Paris MSS. of Elements, (p) 49
Paris MSS. of Elements, (q) 50
Pasch, M. 157 228 250
Pediasimus, Joannes 72—73
Peithon 203
Peletarius (Jacques Peletier) 103 104 249 407
Pena 104
Perpendicular  "plane" and "solid" 272 "plane" and "solid" 272
Perpendicular  definition 181 definition 181
Perpendicular  perpendicular and obliques 291 perpendicular and obliques 291
Perseus 42 162—163
Pesch, J.G. van, De Prodi fontibus 23sqq. 29n.
Petrus Montaureus (Pierre Mondore) 102
Peyrard and Vatican MS. 190
Peyrard and Vatican MS. (P) 46 47 103 108
Pfleiderer, C.F. 168 298
Phaenomena of Euclid 16 17
Philippus of Mende I 116
Phillips, George 112
Philo of Byzantium 20 23
Philo, proof of I. 8 263—264
Philolaus 34 351 371 399
Philoponus 45 191—192
Pirckenstein, A.E. Burkh. von 107
Plane (or plane surface), "Plane loci" 329—330
Plane (or plane surface), "Plane problems" 329
Plane (or plane surface), "Simson's" definition and Gauss on 172—173
Plane (or plane surface), Archimedes' assumption 171 172
Plane (or plane surface), Beez 176
Plane (or plane surface), Crelle's tract on 172—174
Plane (or plane surface), Deahna 174
Plane (or plane surface), Enriques and Amaldi, Ingrami, Veronese and Hilbert on 175
Plane (or plane surface), evolution of, by Bolyai and Lobachewsky 174—175
Plane (or plane surface), J.K. Becker 174
Plane (or plane surface), Leibniz 176
Plane (or plane surface), other ancient definitions of, in Proclus, Heron, Theon of Smyrna, an-Nairizi 171—172
Plane (or plane surface), other definitions by Fourier 173
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 , different senses
, different senses  , a certain curve used by Eudoxus
, a certain curve used by Eudoxus 
 , theory of, rebutted
, theory of, rebutted  by means of "side-" and " diagonal-" numbers
by means of "side-" and " diagonal-" numbers 

 isosceles right-angled triangle
isosceles right-angled triangle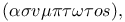 secant
secant 
 , incomposite
, incomposite  "forming a figure"
"forming a figure"  , determinate
, determinate  , indeterminate
, indeterminate 
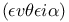 , curved
, curved  , circular
, circular 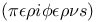 , spiral-shaped
, spiral-shaped  bent
bent  , broken
, broken  , round
, round 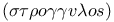
 and loci
and loci  as an area which is locus of area (parallelogram or triangle)
as an area which is locus of area (parallelogram or triangle)  (2),
(2),  (3),
(3), 
 , in logic (Aristotle)
, in logic (Aristotle)  "plane" and "solid"
"plane" and "solid"