|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Johnstone P.T. — Sketches of an Elephant: A Topos Theory Compendium |
|
|
 |
| Предметный указатель |
 -pretopos A1.4.19 -pretopos A1.4.19
 -pretopos, -pretopos,  -indexed B3.3.9 -indexed B3.3.9
 -calculus D4.2.1 -calculus D4.2.1
 -calculus, extended D4.2.16 -calculus, extended D4.2.16
 -calculus, typed D4.2.1 -calculus, typed D4.2.1
 -calculus, untyped D4.2.16 -calculus, untyped D4.2.16
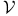 -category B2.1.1 -category B2.1.1
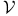 -embedding B2.1.1 -embedding B2.1.1
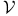 -enrichment B2.1.2 -enrichment B2.1.2
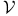 -functor B2.1.1 -functor B2.1.1
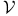 -natural transformation B2.1.1 -natural transformation B2.1.1
 -calculus D4.4.1 -calculus D4.4.1
 -calculus, cartesian D4.4.5 -calculus, cartesian D4.4.5
 -calculus, full D4.4.5 -calculus, full D4.4.5
 -pretopos A1.4.19 -pretopos A1.4.19
 -structure D1.2.1 D4.1.4 -structure D1.2.1 D4.1.4
 -structure, homomorphism of D1.2.1 -structure, homomorphism of D1.2.1
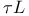 -calculus D4.3.16 -calculus D4.3.16
 -calculus D4.3.1 -calculus D4.3.1
2-category B1.1.1
2-category, locally ordered A3.1.2
2-cell B1.1.1
2-functor B1.1.2
Adjoint (in a 2-category) B1.1.2
Adjoint (in a 2-category), weak B1.1.8
Adjoint retract B1.1.9
Algebra (for algebraic theory) D1.2.15(a)
Algebra (for algebraic theory), free D5.3.5
Algebra (for an endofunctor) A1.1.4
Allegory A3.2.1
Allegory, distributive A3.2.13
Allegory, division A3.4.1
Allegory, effective A3.3.9
Allegory, geometric A3.2.12
Allegory, positive geometric A3.2.12
Allegory, positive union A3.2.11
Allegory, power A3.4.5
Allegory, pre-tabular A3.3.6
Allegory, syntactic D1.4.15 D4.3.9
Allegory, tabular A3.2.3
Allegory, union A3.2.11
Apartness relation D4.7.6
Arithmetic operations A2.5.4
Arithmetic operations on numerals D5.5.14
Arithmetic operations on R D4.7.8
Arity D1.1.1
Associated sheaf functor A4.1.8 A4.4.4 C2.2.6
Associated split fibration B1.3.10
atom C3.5.7
Atomic proposition D1.1.1
Atomic system D3.4.13
Atomic topos C3.5.1
Axiom of Choice D4.5.1(b) D4.5.4
Axiom of theory D1.1.6
Axiom, distributive D1.3.1(i)
Axiom, Frobenius D1.3.1(i)
Axiom, geometric B4.2.7(b)
Axiom, identity D1.3.1(a)
Axiom, logical D1.3.1
Axiom, non-logical D1.1.6
Bag of T-models B4.4.15
Bagdomain, lower B4.4.17
Bagdomain, upper B4.4.21(c)
Basis (for locale) C2.2.4(b)
Beck-Chevalley condition A1.4.11 A2.2.4 A4.1.16 B1.4.2
Beck-Chevalley condition, weak A4.1.16
Beck-Chevalley morphism C2.4.16
Beck-Chevalley morphism, stable C2.4.16
Beck-Chevalley morphism, weak C2.4.16
Beth Definability Theorem D3.5.2
Bicategory B1.1.2
Bimodule (between internal categories) B2.7.1
Biseparated functor C2.2.13
Bisite C2.2.13
Bound (for topos over  ) B3.1.7 ) B3.1.7
Bound (for topos over  ), pre- D3.2.3 ), pre- D3.2.3
C-monoid D4.2.15
Cantor diagonal argument D4.1.8
Cantor-Bernstein theorem D4.1.11
capitalization D1.5.3
Cardinal, finite A2.5.14 D5.2.1
Cardinal, generic finite A2.5.14
Cardinal, limit power A2.1.2
Cartesian closed category A1.5.1
Cartesian closed category, locally A1.5.3
Cartesian closed category, properly A1.5.1
Category,  -accessible D2.3.1 -accessible D2.3.1
Category,  -filtered D2.3.1 -filtered D2.3.1
Category,  -Heyting D3.1.19 -Heyting D3.1.19
Category, 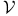 -enriched B2.1.1 -enriched B2.1.1
Category,  -coherent A1.4.19 -coherent A1.4.19
Category, *-autonomous C1.1.7
Category, accessible D2.3.1
Category, balanced A1.1.1
Category, Barr-exact A1.3.6
Category, Boolean coherent A1.4.10
Category, cartesian A1.2.1
Category, cartesian closed A1.5.1
Category, Cauchy-complete A1.1.10
Category, co-slice A1.1.6
Category, coherent A1.4.1
Category, concrete A1.1.5
Category, continuous C4.2.7
Category, cowell-powered A1.4.17
Category, disjunctive B1.5.10 D1.3.6
Category, effective regular A1.3.6
Category, enriched B2.1.1
Category, essentially small B2.3.4
Category, exact A1.3.6
Category, generated by a protocategory A1.1.5
Category, geometric A1.4.18
Category, Grothendieck B1.3.1
Category, Hey ting A1.4.10
Category, ind-small C4.2.18
Category, indexed B1.2.1
Category, internal B2.3.1(a)
Category, Karoubian A1.1.10
Category, lextensive B1.5.10 D1.3.6
Category, locally cartesian A1.2.6
Category, locally cartesian closed A1.5.3
Category, locally internal B2.2.1
Category, locally presentable B4.5.2 D2.3.6
Category, locally small A1.1.1 B1.3.12
Category, logical A1.4.1
Category, partial D3.1.8
Category, positive coherent A1.4.4
Category, properly cartesian closed A1.5.1
Category, regular A1.3.3
Category, simply connected A1.2.9
Category, sketchable D2.3.8
Category, slice A1.1.6
Category, small A1.1.1
Category, stiff B1.3.11
Category, strongly connected A4.6.9 D3.1.7
Category, structured over 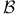 A1.1.5 A1.1.5
Category, suitable for  D4.1.4 D4.1.4
Category, syntactic D1.4.1 D4.2.4 D4.3.4 D4.4.7
Category, well-copowered A1.4.17
Category, well-powered A1.4.17 B1.3.14
Centre (of local morphism) C3.6.2
Characteristic morphism A1.6.1
Choice, axiom of D4.5.4
Choice, dependent D4.5.16
Choice, external D4.5.4
Choice, internal D4.5.1(b)
Classifying map (of subobject) A1.6.1
Classifying topos B4.2.1(b) D3.1.1
Classifying topos for atomless Boolean algebras D3.4.12
Classifying topos for cartesian theory D3.1.1
Classifying topos for coherent theory D3.1.9
| Classifying topos for decidable objects D3.2.7
Classifying topos for dense linearly ordered objects D3.4.11
Classifying topos for geometric theory B4.2.9 D3.1.12
Classifying topos for infinite decidable objects D3-4.10
Classifying topos for K-finite objects D3.2.10
Classifying topos for objects B3.2.9 D3.2.1
Classifying topos for partial equivalence relations on N C5.2.8(c)
Classifying topos for partial surjections 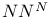 D4.1.9 D4.1.9
Classifying topos for propositional theory B4.2.12
Classifying topos for regular theory D3.1.4
Classifying topos for subobjects of I B3.2.10
Classifying topos for subterminal objects B3.2.11
Classifying topos, Boolean D3.4.3
Cleavage B1.3.4
Cleavage, normalized B1.3.4
Closed subgroup theorem C5.3.2
Closure (of subtopos) A4.5.20
Closure operation, universal A4.3.2
Co-bag of 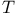 -models B4.4.21(b) -models B4.4.21(b)
Coadjoint retract B1.1.9
Cocomplete object (in 2-category) B1.1.16
Cocomplete object (in 2-category), injective B1.1.16
Cocomplete object (in 2-category), linearly B1.1.16
Cocomplete object (in 2-category), pointwise B1.1.16
Coherent category A1.4.1
Coherent category, Boolean A1.4.10
Coherent category, positive A1.4.4
Colocalization C3.6.19
Comma object B1.1.4(c)
Comonad, cartesian A4.2.1
Comonad, idempotent B1.1.9(c)
Comorphism of sites C2.3.18
Comparison lemma C2.2.3
Completeness Theorem for  -calculus D4.2.6 -calculus D4.2.6
Completeness Theorem for 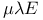 -caIculus D4.4.9 -caIculus D4.4.9
Completeness Theorem for 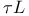 -calculus D4.3.19(b) -calculus D4.3.19(b)
Completeness Theorem for  -calculus D4.3.11 -calculus D4.3.11
Completeness Theorem for cartesian logic D1.4.6 D1.5.1
Completeness Theorem for coherent logic D1.4.11 D1.5.10
Completeness Theorem for first-order logic D1.4.11 D1.5.14 D3.1.18
Completeness Theorem for geometric logic D1.4.11 D3.1.16
Completeness Theorem for regular logic D1.4.11 D1.5.4
Completeness Theorem, Classical D1.5.4 D1.5.10 D1.5.14 D3.1.16
Completeness Theorem, conceptual D3.5.9
Completeness Theorem, functional D1.3.12 D3.1.3
Composition predicate A1.1.5
Comprehension scheme B1.3.12
Comprehensive factorization B2.5.11
Condition (PCC) B4.4.4
Cone in sketch D2.1.1
Cone, discrete D2.1.1
Cone, lax B1.1.6
Cone, weighted B1.1.3
Constant symbol D1.1.1
context D1.1.4 D4.4.2
Context, canonical D1.1.4
Context, suitable D1.1.4
Continuous G-set A2.1.6
Continuous G-set, uniformly A2.1.7
Continuous map (of locales) C1.2.1
Continuous map (of locales), closed C3.2.1
Continuous map (of locales), minimal surjective D4.6.8
Continuous map (of locales), open C1.5.3
Continuous map (of locales), perfect C3.2.9
Continuous map (of locales), proper C3.2.5
Continuous map (of locales), separated C3.2.9
Continuous map (of locales), triquotient C3.2.7
Coproduct,  -indexed B1.4.4 -indexed B1.4.4
Coproduct, disjoint A1.4.4
Coproduct, disjoint  -indexed B1.4.11 -indexed B1.4.11
Coproduct, quasi-disjoint A1.5.14
Coproduct, stable  -indexed B1.4.10 -indexed B1.4.10
Core (in allegory) A3.3.1
Coreflexive pair A1.2.10
Cosieve A1.6.6 A4.5.2
Cotensor B1.1.4(b)
Cover A1.3.2
Coverage A2.1.9 C2.1.1
Coverage, canonical C2.1.11
Coverage, chaotic C2.2.14(a)
Coverage, coherent A2.1.11(b) C2.1.12(d)
Coverage, dm- C3.2.18
Coverage, Grothendieck C2.1.8
Coverage, induced C2.2.2
Coverage, pre-canonical C2.1.12(d)
Coverage, regular A2.1.11(a) C2.1.12(b)
Coverage, rigid C2.2.18(b)
Coverage, separated C2.1.11
Coverage, sifted C2.1.3
Coverage, subcanonical C2.1.11
Coverage, Zariski A2.1.11(f) D3.1.11(a)
Covering family A1.3.2 A2.1.9 C2.1.1
Curry-Howard isomorphism D4.2.1
de Morgan’s law D4.6.2
De Morgan’s law, strong D4.6.6
De Morgan’s law, weak D4.6.4
Decalage B2.5.4(b)
Dedekind section D4.7.4
Definability (in fibration) B1.3.15
Definability Theorem D3.5.1
Derivation D1.3.1
Descent condition B1.5.2
Descent condition, effective B1.5.2
Descent data B1.5.1
Descent morphism B1.5.5
Diaconescu’s theorem B3.2.7
Diagram in directed graph D2.1.1
Diagram in indexed category B2.3.11
Diagram, constant B2.5.4(a)
Diagram, lax B1.1.6
Diagram, weighted B1.1.3
Diers completion D3.2.8
Direct image A4.1.1(a)
Dissolution (of locale) C1.2.13
Distribution (on topos) B4.5.8
distributor B2.7.1
Doctrine B1.1.11
Domain C1.1.3
Double coset D3.4.1
Edwards criterion C3.4.4
Effectivization A3.3.10
Eilenberg-Moore object B1.1.7
Embedding (of structures) D1.2.10(c)
Embedding (of structures), elementary D1.2.10(b)
Epimorphism, extremal A1.3.2
Epimorphism, regular A1.3.2
Epimorphism, strong A1.3.2
Equifier B1.1.4(f)
Equivalence (in 2-category) B1.1.2
Equivalence (in 2-category), strong B1.1.2
Equivalence (in allegory) A3.3.1
Equivalence (of categories) A1.1.1
Equivalence (of categories), weak A1.1.1
Equivalence (of theories) D1.3.7(b)
Equivalence (of theories), Morita D1.4.9 D1.4.13
Equivalence relation A1.3.6
Equivalence relation, effective A1.3.6
Equivalence relation, strong C2.2.13
Equivalence sieve C3.4.5
Espace etale C1.3.3
Etale completion C5.3.16
Etale morphism C1.3.3
Etendue C5.2.4
Excluded middle, law of D1.3.3
Exponential ideal A1.5.10
Exponential transpose A1.5.1
Exponential variety C5.4.1
Exterior (of subtopos) A4.5.19
Factorization theorem for locally connected morphisms C3.3.5
Factorization theorem for pre-geometric morphisms A4.1.13
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -pretopos
-pretopos  -indexed
-indexed  -calculus
-calculus 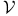 -category
-category  -calculus
-calculus  -pretopos
-pretopos  -structure
-structure 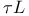 -calculus
-calculus  -calculus
-calculus  -accessible
-accessible 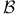
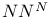
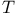 -models
-models 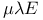 -caIculus
-caIculus