|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Johnstone P.T. — Sketches of an Elephant: A Topos Theory Compendium |
|
|
 |
| Предметный указатель |
Factorization theorem for tidy morphisms C3.4.15
Factorization theorem, closed inclusion-totally connected C3.6.17(d)
Factorization theorem, comprehensive B2.5.11
Factorization theorem, direct image-inverse image A4.1.12
Factorization theorem, hyperconnected-localic A4.6.5
Factorization theorem, open inclusion-local C3.6.3(f)
Factorization theorem, pure-entire C3.4.13
Factorization theorem, surjection-inclusion A4.2.10
Fibration B1.3.4
Fibration in 2-category B4.4.1
Fibration of sites C2.5.6
Fibration, associated split B1.3.10
Fibration, cartesian B1.4.1
Fibration, cloven B1.3.4
Fibration, continuous C2.5.6
Fibration, discrete B1.3.11 B2.5.1
Fibration, interval C2.1.13
Fibration, locally small B1.3.12
Fibration, satisfying (PCC) B4.4.4
Fibration, split B1.3.4
Fibration, stiff B1.3.11
Fibration, well-powered B1.3.14
Field D1.1.7(h)
Field, coherent D1.1.7(h)
Field, residue D4.7.9
Filter, completely prime C1.2.1
Filter, neighbourhood C1.2.1
Filterpower A2.1.13
Filterquotient construction A2.1.13
Finite cardinal A2.5.14 D5.2.1
Finite cardinal, generic A2.5.14
Finite object, 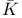 - D5.4.22 - D5.4.22
Finite object, Dedekind- A1.6.10 D5.1.4 D5.2.9
Finite object, Kuratowski- D1.1.7(k) D5.4.1(b)
Finite object, Russell- D5.5.12
Finite object, Sierpinski- D5.4.1
Fixset C1.1.13
Fixset, dense C1.1.16(c)
Formula D1.i.3 D4.1.3
Formula in context D1.1.4
Formula, 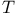 -complete D3.4.13 -complete D3.4.13
Formula, atomic D1.1.3 D4.1.3
Formula, cartesian D1.1.7(m) D1.3.4
Formula, closed D1.1.3
Formula, coherent D1.1.3
Formula, complete D3.4.13
Formula, disjunctive D1.3.6
Formula, first-order D1.1.3
Formula, geometric D1.1.3
Formula, Horn D1.1.3
Formula, provably equivalent D1.3.7(a)
Formula, regular D1.1.3
Formula, well-formed D1.1.3
Frame A3.2.2(b) C1.1.1
Frame, coherent C2.4.3
Frame, consistent C2.4.9
Frame, Giraud B4.5.1
Frame, internal C1.6.1
Frame, nontrivial C2.4.9
Frame-valued set A3.3.13 C1.3.3
Frame-valued set, complete C1.3.6
Free topos D4.3.14(a)
Free topos with natural number object D4.3.19(d)
Frobenius reciprocity A1.3.3 A1.5.8
Function symbol D1.1.1 D4.1.1
Functional completeness D1.3.12 D3.1.3 D4.2.10
Functional extension (of theory) B4.2.7(a)
Functor between 2-categories B1.1.2
Functor,  -continuous D2.3.4 -continuous D2.3.4
Functor,  -Heyting D3.1.19 -Heyting D3.1.19
Functor,  -continuous B1.4.13 -continuous B1.4.13
Functor, 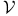 -enriched B2.1.1 -enriched B2.1.1
Functor, 2-initial B3.4.11
Functor, accessible B3.1.12
Functor, bicartesian D5.1.8
Functor, biseparated C2.2.13
Functor, cartesian A1.2.1
Functor, cartesian closed A1.5.2
Functor, cocontinuous (between sites) C2.3.18
Functor, cofinal B2.5.12
Functor, coherent A1.4.4
Functor, conservative A1.1.1
Functor, continuous (between sites) C2.3.1
Functor, continuous (indexed) B1.4.13
Functor, cover-creating C3.5.10
Functor, cover-preserving C2.3.1
Functor, cover-reflecting C2.3.18
Functor, direct image A4.1.1(a) C1.4.3
Functor, essentially surjective A1.1.1
Functor, faithful A1.1.1
Functor, final B2.5.12
Functor, finitely covering D3.5.7
Functor, flat C2.3.7
Functor, full on subobjects D3.5.6
Functor, Heyting A1.4.10
Functor, indexed B1.2.1
Functor, initial B2.5.11
Functor, internal B2.3.1(b)
Functor, inverse image A4.1.1(a) C1.4.1
Functor, lax B1.1.2
Functor, left exact A1.2.1
Functor, locally internal B2.2.1
Functor, logical A2.1.1
Functor, monadic A1.1.2
Functor, regular A1.3.3
Functor, separated A2.6.4(d) C2.1.2
Functor, strict B1.1.2
Functor, strong B2.1.4
Functor, sub-cartesian-closed C3.1.1
Functor, sub-logical C3.1.1
Functor, tripleable A1.1.2
Fundamental Theorem of topos theory A2.3.2
G-set A2.1.4
G-set, continuous A2.1.6
G-set, effective B3.2.4(b)
G-set, transitive B3.2.4(b)
G-set, uniformly continuous A2.1.7
G-torsor B3.2.4(b)
Generating family A1.2.4
Generator A1.2.4
Geometric category A1.4.18
Geometric category,  -positive A1.4.19 -positive A1.4.19
Geometric construct B4.2.5
Geometric construct, coherent B4.3.8
Geometric morphism A4.1.1(a)
Geometric morphism,  -essential B3.1.1 -essential B3.1.1
Geometric morphism,  -indexed B3.1.2 -indexed B3.1.2
Geometric morphism, atomic C3.5.1
Geometric morphism, Beck-Chevalley C2.4.16
Geometric morphism, bounded B3.1.7
Geometric morphism, closed C3.2.3
Geometric morphism, connected C1.5.7
Geometric morphism, descent C5.1.1
Geometric morphism, embedding A4.2.9
Geometric morphism, entire B4.4.21(a)
Geometric morphism, essential A4.1.5
Geometric morphism, hyperconnected A4.6.3
Geometric morphism, hyperlocal B4.4.19
Geometric morphism, inclusion A4.2.9
Geometric morphism, lax descent C5.1.8
Geometric morphism, local C3.6.1
Geometric morphism, localic A4.6.1
Geometric morphism, locally connected C3.3.1
Geometric morphism, minimal surjective D4.6.8
Geometric morphism, open C1.5.4 C3.1.7
Geometric morphism, partial A4.1.13
Geometric morphism, pre-descent C5.1.1
Geometric morphism, proper C3.2.12(a)
Geometric morphism, pure C3.4.12
Geometric morphism, separated C3.2.12(b)
| Geometric morphism, skeletal D4.6.9
Geometric morphism, stably closed C3.2.26
Geometric morphism, surjection A4.2.6
Geometric morphism, tidy C3.4.2
Geometric morphism, totally connected C3.6.16
Geometric morphism, weak Beck—Chevalley C2.4.16
Geometric quotient B4.2.7(b)
Geometric theory B4.2.7(c) D1.1.6
Geometric theory, dualizable B4.3.2
Geometric theory, prepositional B4.2.12 D1.1.7(m)
Geometric transformation A4.1.1(b)
Giraud frame B4.5.1
Giraud frame, symmetric B4.5.4
Giraud’s Theorem B3.3.4 B3.3 11 C2.2.8
Giraud’s Theorem, little C2.1.11
Gleason cover D4.6.8
Glued topos A2.1.12
Glueing construction A2.1.12
Godel’s Incompleteness Theorem D4.3.19(d)
Graph of morphism A3.1.3
Graph, directed D2.1.1
Graph, undirected D3.2.7
Grothendieck construction A1.1.7 B1.3.1
Grothendieck coverage C2.1.8
Grothendieck topology A2.1.9
Grothendieck topos C2.2.9
Groupoid, internal B2.3.12(c)
Groupoid, localic C5.2.11
Heine-Borel Theorem D4.7.4
Heyting algebra A1.5.11
Heyting algebra, irreducible A2.6.4(e)
Heyting category A1.4.10
Heyting semilattice A1.5.11
Higgs object D4.5.10
Hyperconnected-localic factorization A4.6.5
Ideal for coverage C1.1.16(e) C2.3.21
Ideal in poset B3.2.4(d) C1.1.3
Ideal, exponential A1.5.10
Ideal, maximal D4.6.14
Ideal, prime D4.6.14
Ideal, proper D4.6.14
Idempotent A1.1.8
Idempotent (in 2-category) B1.1.9
Idempotent monad B1.1.9
Idempotent monad, associated A4.3.11
Idempotent, split A1.1.8
Idempotent, symmetric A3.3.2
Identifier B1.1.4(e)
Image A1.3.1
Image, direct A4.1.1
Image, inverse A4.1.1
Inclusion (geometric) A4.2.9
Indexed category B1.2.1
Indexed category, cartesian B1.4.1
Indexed category, complete B1.4.2
Indexed category, essentially small B2.3.4
Indexed category, locally small B1.3.12
Indexed category, well-powered B1.3.14
Indexing, canonical B1.2.2(c)
Indexing, naive B1.2.2(a)
Inductive completion C4.2.1
inserter B1.1.4(d)
Interior (of subtopos) A4.5.19
Internal category B2.3.1(a)
Internal category, connected B2.5.6
Internal category, discrete B2.3.12(a)
Internal category, filtered B2.6.2(a)
Internal category, indiscrete B2.3.4
Internal category, weakly filtered B2.6.2(b)
Internal full subcategory B2.3.5
Internal groupoid B2.3.12(c)
Internal language D1.3.11 D4.1.8
Internal poset B2.3.8
Internal poset, complete B2.3.9
Internal poset, conditionally complete D4.7.7
Internal poset, Dedekind-complete D4.7.7
Internal poset, directed B2.6.2
Internal poset, DM-separated D4.7.15
Internal site C2.4.1
Internalization C1.6.1
Interpolation property C4.1.2 C4.2.15
Interpretation (in structure) D1.2.3 D1.2.6 D4.1.5
Interpretation (in structure), Brouwer-Heyting-Kolmogorov D1.2.2
Interpretation (in structure), Tarski D1.2.1
Interval (in poset) C2.1.13
Inverse image A4.1.1(a)
Inverter B1.1.4(e)
Iterator D4.1.2(ix)
Joyal’s Lemma C4.1.15
Kan extension A4.1.4
Kan extension, internal B2.3.20
Knaster-Tarski Theorem D4.1.10
Kock-Zoeherlein monad B1.1.11
KZ-monad B1.1.11
L-valued matrix A3.2.2(b)
L-valued set A3.3.13
Language, first-order D1.1.1
Language, higher-order D4.1.1
Language, internal D1.3.11 D4.1.8
Lattice, continuous C4.1.1(c)
Lattice, distributive C1.1.3
Lattice, stably continuous C4.1.10
Lawvere-Tierney topology A4.4.1
Lax functor B1.1.2
Lax limit B1.1.6
Lax limit, normalized C2.3.15(d)
Lax pullback B1.1.4(c)
Leibniz equality D4.3.2
Limit power cardinal A2.1.2
Limit, conical B1.1.3
Limit, indexed B1.1.3
Limit, lax B1.1.6
Limit, weighted B1.1.3
Lindenbaum algebra D1.4.14
Lindenbaum algebra for Dedekind sections of  D4.7.4 D4.7.4
Lindenbaum algebra for injections  C1.2.9 C1.2.9
Lindenbaum algebra for paradoxical open cover of [0,1] D4.7.13
Lindenbaum algebra for partial surjections  D4.1.9 D4.1.9
Lindenbaum algebra for surjections  C1.2.8 C1.2.8
List object A2.5.15 D4.1.4
Local character condition C2.1.8
Local homeomorphism A1.2.7 C1.3.2 C3.3.4
Local operator A4.4.1
Local operator, closed A4.5.3
Local operator, dense A4.5.20
Local operator, double-negation A4.5.9
Local operator, open A4.5.1
Local operator, pullback A4.5.14(e)
Local operator, quasi-closed A4.5.21
Locale C1.2.1
Locale,  - C1.2.17 - C1.2.17
Locale, coherent C2.4.3
Locale, compact C1.5.5
Locale, connected C1.5.7
Locale, discrete C1.6.4
Locale, exponentiable C4.1.9
Locale, extremally disconnected C1.5.10 D4.6.3(b)
Locale, Hausdorff C1.2.17
Locale, injective C4.1.6
Locale, internal C1.6.1
Locale, local C1.5.6
Locale, locally coherent C4.1.13
Locale, locally compact C4.1.7
Locale, locally connected C1.5.8
Locale, locally metastably compact C4.4.7
Locale, locally stably compact C4.1.11
Locale, open C3.1.16
Locale, regular C1.2.17
Locale, second countable D4.5.2(d)
Locale, spatial C1.2.3 C1.6.5
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



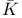 -
-  -complete
-complete  -continuous
-continuous  -continuous
-continuous  -enriched
-enriched  -positive
-positive 



 -
-