|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Johnstone P.T. — Sketches of an Elephant: A Topos Theory Compendium |
|
|
 |
| Предметный указатель |
Sheaf, G-equivariant A2.1.11(c)
Sheafification A4.4.4
Shift (of simplicial object) B2.5.4(b)
Sierpinski topos B3.2.11
Sierpiriski cone A2.1.12 C3.6.3(f)
Sierpiriski space A2.1.12 C1.1.4
Sieve A1.6.6 A4.5.5 C2.1.3
Sieve, closed A2.1.10
Sieve, connected C3.3.10
Sieve, covering C2.1.3
Sieve, dm- C3.2.18
Sieve, effective-epimorphic C2.1.11
Sieve, equivalence C3.4.5
Sifted colimit A1.2.12
Sifted coverage C2.1.3
Signature D1.1.1 D4.1.1
Signature, 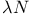 - D4.2.11 (a) - D4.2.11 (a)
Signature,  - D4.2.1 - D4.2.1
Signature,  - D4.4.2 - D4.4.2
Signature, 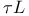 - D4.3.16 - D4.3.16
Signature,  - D4.3.1 - D4.3.1
Signature, canonical D1.3.11 D4.1.7
Signature, first-order D1.1.1
Signature, higher-order D4.1.1
Signature, propositional D1.1.7(m)
Simplicial identities B2.3.2
Simplicial object B2.3.2
Simplicial object, 2-truncated B3.4.11
Simplicial topos B3.4.11
Singleton (in frame-valued set) C1.3.6
Singleton map A2.2.2
Site A2.1.9 C2.1.1
Site of definition C2.2.15
Site, atomic C3.5.8
Site, consistent C2.4.8
Site, essentially small C2.2.3
Site, internal C2.4.1
Site, local C3.6.3(d)
Site, locally connected C3.3.10
Site, small C2.1.1
Site, standard A2.1.11(a) C2.1.11
Site, syntactic D3.1.1
Sketch D2.1.1(a)
Sketch,  -coherent D2.2.9 -coherent D2.2.9
Sketch, coherent D2.1.2(g)
Sketch, colimit D2.1.2(b)
Sketch, coproduct D2.1.2(c)
Sketch, disjunctive D2.1.2(e)
Sketch, finitary D2.1.2(d)
Sketch, finite limit D2.1.2(b)
Sketch, finite product D2.1.2(b)
Sketch, geometric D2.1.2(h)
Sketch, inductive D2.1.2(c)
Sketch, limit D2.1.2(b)
Sketch, linear D2.1.2(a)
Sketch, mixed D2.1.2(d)
Sketch, product D2.1.2(b)
Sketch, projective D2.1.2(b)
Sketch, regular D2.1.2(f)
Slice category A1.1.6
Sobrification C1.2.3
Sorgenfrey plane D4.5.2(e)
sort D1.1.1 D4.1.1
Soundness Theorem D1.3.2 D4.2.3 D4.3.3 D4.4.6
Source-target predicate A1.1.5
Space, 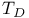 - C1.2.5 - C1.2.5
Space, Choquet A2.6.4(b)
Space, coherent D3.3.14
Space, extremally disconnected C1.5.10
Space, Fhkihet A2.6.4(c)
Space, injective C4.1.6
Space, local C1.5.6
Space, sober C1.2.3
Span (in a category) A3.3.8
STACK B1.5.2
Stone algebra D4.6.1
Strength (of functor) B2.1.4
Structure (for signature) D1.2.1 D4.1.4 D4.4.3
Subcategory, definable B1.3.16
Subcategory, dense C4.2.18 D2.3.2(iii)
Subcategory, dense (for coverage) C2.2.1
Subcategory, full A1.1.1
Subcategory, internal full B2.3.5
Subcategory, reflective A1.1.1
Subcategory, replete A1.1.1
Subclosure C1.2.5
Subfibration B1.3.16
Subfibration, definable B1.3.16
Sublocale C1.2.5
Sublocale, closed C1.2.6(b)
Sublocale, complemented C1.2.11
Sublocale, dense C1.2.6(c)
Sublocale, fibrewise closed C1.2.14
Sublocale, fibrewise dense C1.2.14
Sublocale, open C1.2.6(a)
Submersion C1.6.7
Subobject A1.3.1
Subobject classifier A1.6.1
Subobject classifier, weak A2.6.1
Subobject, closed A4.3.2
Subobject, complemented A1.4.10
Subobject, dense A4.3.2
Subobject, effective C3.4.5
Subobject, generic A1.6.1
Subobject, negation of A1.4.13
Subobject, widespread A1.6.11
Subquotient A4.6.1
Substitution (in formal language) D1.1.4
Substitution property D1.2.4 D1.2.7 D4.1.6
Substructure D1.2.10(c)
Subtopos A4.3.9
Subtopos, Boolean A4.5.21
Subtopos, closed A4.5.3
Subtopos, closure of A4.5.20
Subtopos, dense A4.5.20
Subtopos, exterior of A4.5.19
Subtopos, geometric A4.3.9
Subtopos, interior of A4.5.19
Subtopos, logical A4.3.9
Subtopos, open A4.5.1
| Subtopos, quasi-closed A4.5.21
Superdense C1.5.2
Support of an object A1.3.8
Supports split D4.5.1(a)
Surjection (geometric) A4.2.6
Surjection-inclusion factorization A4.2.10
Syntactic category for  -theory D4.2.4 -theory D4.2.4
Syntactic category for  -theory D4.4.7 -theory D4.4.7
Syntactic category for  -theory D4.3.4 -theory D4.3.4
Syntactic category for cartesian theory D1.4.1
Syntactic category for coherent theory D1.4.10
Syntactic category for first-order theory D1.4.10
Syntactic category for geometric theory D1.4.10
Syntactic category for regular theory D1.4.10
tabulation A3.1.1 A3.2.3
Tensor (in 2-category) B1.1.4(b)
Tensor condition B4.4.5
Term (in formal language) D1.1.2 D4.1.2
Term (in formal language) in context D1.1.4
Term (in formal language),  - D4.2.1 - D4.2.1
Term (in formal language), closed D1.1.3
Term constructor D4.1.2
Term declaration D4.4.2
Theory B4.2.1(a) D1.1.6
Theory of objects B4.2.4(a) D3.2.1
Theory over S B4.2.1(a)
Theory, 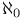 -categorical D3.4.7 -categorical D3.4.7
Theory,  - D4.2.2 - D4.2.2
Theory,  D4.4.4 D4.4.4
Theory,  -coherent D2.2.9 -coherent D2.2.9
Theory, 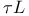 - D4.3.16 - D4.3.16
Theory,  - D4.3.3 - D4.3.3
Theory, algebraic D1.1.7(a) D5.3.1
Theory, cartesian D1.1.7(m) D1.3.4
Theory, coherent B4.3.8 D1.1.6
Theory, complete D3.4.7
Theory, disjunctive D1.3.6
Theory, equivalent D1.3.7(b)
Theory, first-order D1.1.6
Theory, geometric B4.2.7(c) D1.1.6
Theory, Horn D1.1.6
Theory, internal algebraic D5.3.9
Theory, model-complete D3.4.9
Theory, prepositional B4.2.12 D1.1.7(m)
Theory, regular D1.1.6
Topological group, coherent D3.4.1
Topological group, nearly discrete A2.1.6
Topological group, pro-discrete A2.1.6
Topology, Grothendieck A2.1.9
Topology, Lawvere-Tiemey A4.4.1
Topos A2.1.1
Topos,  -indexed B3.1.2 -indexed B3.1.2
Topos, 2-valued A2.1.13
Topos, atomic C3.5.1
Topos, bounded over  B3.1.7 B3.1.7
Topos, classifying B4.2.1(b) D3.1.1
Topos, coherent D3.3.1
Topos, compact C3.2.12(a)
Topos, defined over S B3.1.1
Topos, exponentiable B4.3.1 C4.4.1
Topos, free D4.3.14(a) D4.3.19(d)
Topos, glued A2.1.12
Topos, Grothendieck C2.2.9
Topos, grouplike C3.6.9
Topos, Hausdorff C3.2.12(b)
Topos, having enough points C2.2.12
Topos, hyperlocal B4.4.19
Topos, injective C4.3.1
Topos, Jonsson-Tarski A2.1.11(i)
Topos, local C3.6.2
Topos, locally decidable C5.4.1
Topos, locally orderable C5.4.8
Topos, measure B4.5.8
Topos, quasi-injective C4.3.9
Topos, regular D3.3.1
Topos, Schanuel A2.1.11(h)
Topos, Sierpinski B3.2.11
Topos, simplicial B3.4.11
Topos, standard D5.1.7
Topos, strongly compact C3.4.1
Topos, symmetric B4.5.4
Topos, totally connected C3.6.16
Topos, weak A2.1.1
Topos, Zariski A2.1.11(f)
Torsor B3.2.3
Torsor,  - D2.3.3 - D2.3.3
TYPE D1.1.1 D4.1.1
Type constructor D4.1.1
Type declaration D4.4.2
Type, basic D4.1.1
Type, dependent product D4.4.1
Type, dependent sum D4.4.1
Type, equality D4.4.2(g)
Type, function D4.1.1
Type, list D4.1.1
Type, Mal’cev D4.2.15
Type, power D4.1.1
Type, product D4.1.1
Type, unit D4.4.2(f)
Ultrapower A2.1.13
Ultraproduct D2.4.11
Union (of subobjects) A1.4.1
Union (of subobjects), effective A1.4.3
Unit (in allegory) A3.2.8
Universal closure operation A4.3.2
Universal closure operation, proper A4.4.2
Universal closure operation, strict A4.4.2
Variable D1.1.2
Variable, bound D1.1.3
Variable, free D1.1.3
Wavy arrow C4.2.12
Way below C4.1.1(a)
Weak adjoint B1.1.8
Weak equivalence A1.1.1
Weak equivalence of localic groupoids C5.3.12
Weak subobject classifier A2.6.1
Weak topos A2.1.1
Weakening Property D1.2.4
Wff D1.1.3
Yoneda profunctor B2.7.2
Zorn’s Lemma D4.5.14
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



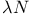 -
- -
-  -
- 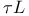 -
-  -
-  -coherent
-coherent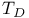 -
-  -categorical
-categorical  -indexed
-indexed  -
-