|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics. Vol. 2 |
|
|
 |
| Предметный указатель |
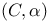 -suinmation 379.M -suinmation 379.M
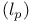 or or 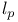 (a sequence space) 168.B (a sequence space) 168.B
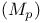 , ultradistribution of class 125.U , ultradistribution of class 125.U
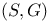 -valued random variable 342.C -valued random variable 342.C
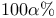 -point 396.C -point 396.C
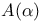 -stability 303.G -stability 303.G
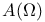 (the totality of functions bounded and continuous on the closure of (the totality of functions bounded and continuous on the closure of  and holomorphic in and holomorphic in  ) 168.B ) 168.B
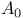 -stability 303.G -stability 303.G
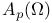 (the totality of functions (the totality of functions 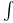 that are holomorphic in that are holomorphic in  and that satisfy and that satisfy 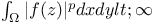 168.B 168.B
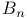 set 22.D set 22.D
 -conjugacy, -conjugacy,  -conjugate 126.B -conjugate 126.B
 -equivalence, -equivalence,  -equivalent 126.B -equivalent 126.B
 -flow 126.B -flow 126.B
 -foliation 154.G -foliation 154.G
 -function in a -function in a  -manifold 105.G -manifold 105.G
 -manifold 105.D -manifold 105.D
 -manifold compact 105.D -manifold compact 105.D
 -manifold paracompact - 105.D -manifold paracompact - 105.D
 -manifold with boundary 105.E -manifold with boundary 105.E
 -manifold without boundary 105.E -manifold without boundary 105.E
 -mapping 105.J -mapping 105.J
 -norm 126.H -norm 126.H
 -structurally stable 126.H -structurally stable 126.H
 -structure 108.D -structure 108.D
 -structure on a topological manifold 114.B -structure on a topological manifold 114.B
 -structure subordinate to (for a -structure subordinate to (for a 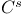 -structure) 108.D -structure) 108.D
 -triangulation 114.C -triangulation 114.C
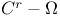 -stable 126.H -stable 126.H
 -function (of many variables) 58.B -function (of many variables) 58.B
 -function (of many variables) germ of (at the origin) 58.C -function (of many variables) germ of (at the origin) 58.C
 -function (of many variables) preparation theorem for 58.C -function (of many variables) preparation theorem for 58.C
 -function (of many variables) rapidly decreasing 168.B -function (of many variables) rapidly decreasing 168.B
 -function (of many variables) slowly increasing 125.O -function (of many variables) slowly increasing 125.O
 -functions and quasi-analytic functions 58 -functions and quasi-analytic functions 58
 -topology, weak 401.C -topology, weak 401.C
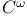 -homomorphism (between Lie groups) 249.N -homomorphism (between Lie groups) 249.N
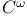 -isomorphism (between Lie groups) 249.N -isomorphism (between Lie groups) 249.N
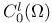 (the totality of functions in (the totality of functions in 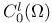 whose supports are compact subsets of whose supports are compact subsets of  ) 168.B ) 168.B
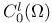 (the totality of l times continuously differentiable functions in (the totality of l times continuously differentiable functions in  ) 168.B ) 168.B
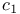 -bundle 237.F -bundle 237.F
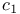 -mapping 237.G -mapping 237.G
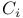 -field 118.F -field 118.F
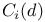 -field 118.F -field 118.F
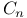 set 22.D set 22.D
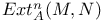 200.G 200.G
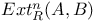 200.K 200.K
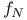 -metric 136.F -metric 136.F
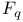 (finite field with q elements) 450.Q (finite field with q elements) 450.Q
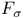 set 270.C set 270.C
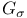 -set 270.C -set 270.C
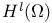 (Sobolev spaces) 168.B (Sobolev spaces) 168.B
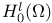 (Sobolev spaces) 168.B (Sobolev spaces) 168.B
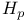 (Hardy spaces) 168.B (Hardy spaces) 168.B
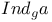 297.G 297.G
 -algebra (of a locally compact Hausdorff group) 36.L -algebra (of a locally compact Hausdorff group) 36.L
 -space, abstract 310.G -space, abstract 310.G
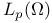 (the space of measurable functions f(x) on (the space of measurable functions f(x) on  such that such that 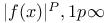 , is integrable) 168.B , is integrable) 168.B
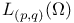 (the Lorentz spaces) 168.B (the Lorentz spaces) 168.B
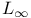 168.B 168.B
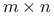 matrix 269.A matrix 269.A
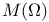 (the set of all essentially bounded measurable factions on (the set of all essentially bounded measurable factions on  ) 168.B ) 168.B
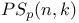 (projective symplectic group over K) 60.L (projective symplectic group over K) 60.L
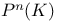 (projective space) 343.H (projective space) 343.H
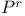 -figure 343.B -figure 343.B
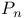 set 22.D set 22.D
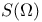 (totality of measurable functions on (totality of measurable functions on  that take finite value almost everywhere) 168.B that take finite value almost everywhere) 168.B
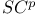 -manifold 178.G -manifold 178.G
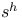 -factorial experiment 102.H -factorial experiment 102.H
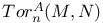 200.D 200.D
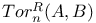 200.K 200.K
 -statistic Hotelling’s 280.B -statistic Hotelling’s 280.B
 -statistic noncentral Hotelling 374.C -statistic noncentral Hotelling 374.C
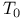 -space 425.Q -space 425.Q
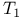 -space 425.Q -space 425.Q
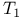 -uniform space 436.C -uniform space 436.C
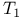 -uniformity 436.C -uniformity 436.C
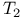 -space 425.Q -space 425.Q
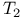 -topological group 423.B -topological group 423.B
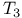 -space 425.Q -space 425.Q
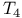 -space 425.Q -space 425.Q
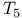 -space 425.Q -space 425.Q
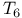 -space 425.Q -space 425.Q
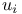 -scale 19.D -scale 19.D
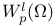 (Sobolev space) 168.B (Sobolev space) 168.B
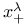 (distribution) 125.EE (distribution) 125.EE
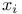 -axis (of a Euclidean space) 140 -axis (of a Euclidean space) 140
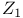 -extension 14.L -extension 14.L
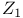 -extension basic 14.L -extension basic 14.L
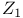 -extension cyclotomic 14.L -extension cyclotomic 14.L
 -capacity 169.C -capacity 169.C
 -excessive function 261.D -excessive function 261.D
 -limit point 126.D -limit point 126.D
 -limit set (of an orbit) 126.D -limit set (of an orbit) 126.D
 -perfect, a-perfectness 186.J -perfect, a-perfectness 186.J
 -point (of a meromorphic function) 272.B -point (of a meromorphic function) 272.B
 -pseudo-orbit 126.J -pseudo-orbit 126.J
 -quartile 396.C -quartile 396.C
 -string 248.L -string 248.L
 -trimmed mean 371.H -trimmed mean 371.H
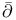 -cohomology groups 72.D -cohomology groups 72.D
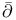 -complex 72.D -complex 72.D
 see “Beta” see “Beta”
 -KMS state 402.G -KMS state 402.G
 -shadowed 126.J -shadowed 126.J
 -traced 126J -traced 126J
 -equivalent (closed on G-manifolds) 431.F -equivalent (closed on G-manifolds) 431.F
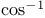 131.E 131.E
 -delta 168.B -delta 168.B
 -measure 270.D -measure 270.D
 -refinement (of a covering) 425.R -refinement (of a covering) 425.R
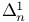 -set 22.D -set 22.D
 see “gamma” see “gamma”
 -equivalent (points) 122.A -equivalent (points) 122.A
 -extension 14.L -extension 14.L
 -matrices, Dirac 415.G -matrices, Dirac 415.G
 -perfect 186.J -perfect 186.J
 -perfectness 186.J -perfectness 186.J
 -point of the kth order (of a holomorphic function) 198.C -point of the kth order (of a holomorphic function) 198.C
 -structure 90.D 105.Y -structure 90.D 105.Y
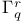 -structure 154.H -structure 154.H
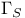 -foliation 154.H -foliation 154.H
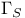 -structure 154.E -structure 154.E
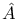 -characteristic class (of a real oriented vector bundle) 237.F -characteristic class (of a real oriented vector bundle) 237.F
 -function 32.C -function 32.C
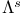 (Lipschitz spaces) 168.B (Lipschitz spaces) 168.B
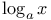 131.B 131.B
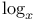 131.D 131.D
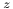 (logarithm) 131.G (logarithm) 131.G
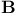 -complete (locally convex space) 424.X -complete (locally convex space) 424.X
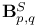 (Besov spaces) 168.B (Besov spaces) 168.B
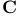 (complex numbers) 74.A 294.A (complex numbers) 74.A 294.A
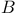 -measurable set 270.C -measurable set 270.C
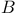 -regular measure 270.F -regular measure 270.F
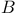 -summable series 379.0 -summable series 379.0
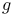 -lattice (of a separable algebra) 27.A -lattice (of a separable algebra) 27.A
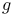 -lattice (of a separable algebra)integral 27.A -lattice (of a separable algebra)integral 27.A
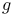 -lattice (of a separable algebra)normal 27.A -lattice (of a separable algebra)normal 27.A
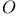 -differential (on an algebraic curve) 9.F -differential (on an algebraic curve) 9.F
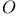 -genus (of an algebraic curve) 9.F -genus (of an algebraic curve) 9.F
 -ideal integrated two-sided 27.A -ideal integrated two-sided 27.A
 -ideal two-sided 27.A -ideal two-sided 27.A
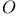 -linearly equivalent divisors (on an algebraic curve) 9.F -linearly equivalent divisors (on an algebraic curve) 9.F
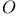 -specialty index (of a divisor of an algebraic curve) 9.F -specialty index (of a divisor of an algebraic curve) 9.F
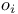 -ideal, left 27.A -ideal, left 27.A
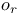 -ideal, right 27.A -ideal, right 27.A
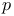 adic exponential valuation 439.F adic exponential valuation 439.F
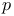 adic extension (of the field of quotients of a Dedekind domain) 439.F adic extension (of the field of quotients of a Dedekind domain) 439.F
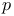 index (of a central simple algebra over a finite algebraic number field) 29.G index (of a central simple algebra over a finite algebraic number field) 29.G
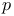 invariant (of a central simple algebra over a finite algebraic number field) 29.G invariant (of a central simple algebra over a finite algebraic number field) 29.G
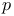 primary ideal 67.F primary ideal 67.F
| 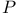 -function, Weierstrass 134.F App. Table -function, Weierstrass 134.F App. Table
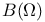 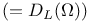 168.B 168.B
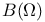 (the space of hyperfunctions) 125.V (the space of hyperfunctions) 125.V
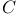 -group 52.M -group 52.M
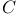 -theory, Serre 202.N -theory, Serre 202.N
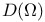 125.B 168.B 125.B 168.B
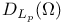 (the totality of functions f(x) in (the totality of functions f(x) in 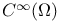 such that for all such that for all 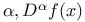 belongs to belongs to 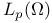 with respect to Lebesgue measure) 168.B with respect to Lebesgue measure) 168.B
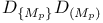 168.B 168.B
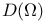 125.B 125.B
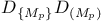 125.U 125.U
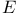 -function 46.C -function 46.C
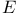 -space 193.N -space 193.N
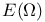 125.I 125.I
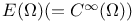 125.I 168.B 125.I 168.B
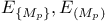 168.B 168.B
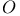 -module 383.I -module 383.I
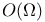 (space of holomorphic functions in (space of holomorphic functions in  ) 168.B ) 168.B
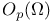 168.B 168.B
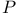 -acyclic 200.Q -acyclic 200.Q
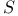 (the totality of rapidly decreasing (the totality of rapidly decreasing  -functions) 168.B -functions) 168.B
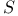 (the totality of tempered distributions) 125.N (the totality of tempered distributions) 125.N
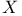 -minimal function 367.E -minimal function 367.E
 -absolutely continuous (additive set function) 380.C -absolutely continuous (additive set function) 380.C
 -completion 270.D -completion 270.D
 -conformal function 352.B -conformal function 352.B
 -constant stratum 418.E -constant stratum 418.E
 -integrable 221.B -integrable 221.B
 -measurable 270.D -measurable 270.D
 -null set 370.D -null set 370.D
 -operator, bounded 356.B -operator, bounded 356.B
 -singular (additive set function) 380.C -singular (additive set function) 380.C
 -conjugate 126.H -conjugate 126.H
 -connected space 79.C -connected space 79.C
 -connected space locally 79.C -connected space locally 79.C
 -consistent (system) 156.E -consistent (system) 156.E
 -equivalent 126.H -equivalent 126.H
 -explosion 126.J -explosion 126.J
 -group 190.E -group 190.E
 -homomorphism (between -homomorphism (between  -groups) 190.E -groups) 190.E
 -isomorphism (between -isomorphism (between  -groups) 190.E -groups) 190.E
 -limit point 126.D -limit point 126.D
 -limit set 126.D -limit set 126.D
 -modules, duality theorem for 422.L -modules, duality theorem for 422.L
 -stability theorem 126.J -stability theorem 126.J
 -stable, -stable,  - 126.H - 126.H
 -subgroup (of an -subgroup (of an  -group) 190.E -group) 190.E
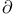 -functor 200.I -functor 200.I
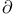 -functor universal 200.I -functor universal 200.I
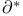 -functor 200.I -functor 200.I
 -group 151.F -group 151.F
 -length (of a group) 151.F -length (of a group) 151.F
 -manifold 114.I -manifold 114.I
 -series(of a group) 151.F -series(of a group) 151.F
 -solvable group 151.F -solvable group 151.F
 -theorem 116 -theorem 116
 -topology 424.R -topology 424.R
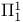 set 22.A set 22.A
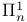 set 22.D set 22.D
 -set 308.I -set 308.I
 -space 425.Y -space 425.Y
 -additive measure 270.D -additive measure 270.D
 -additivity 270.D -additivity 270.D
 -algebra 270.B -algebra 270.B
 -algebra optional 407.B -algebra optional 407.B
 -algebra predictable 407.B -algebra predictable 407.B
 -algebra tail 342.G -algebra tail 342.G
 -algebra topological 270.C -algebra topological 270.C
 -algebra well-measurable 407.B -algebra well-measurable 407.B
 -compact space 425.V -compact space 425.V
 -complete (vector lattice) 310.C -complete (vector lattice) 310.C
 -complete lattice 243.D -complete lattice 243.D
 -complete lattice conditionally 243.D -complete lattice conditionally 243.D
 -discrete (covering of a set) 425.R -discrete (covering of a set) 425.R
 -field Bayer sufficient 396.J -field Bayer sufficient 396.J
 -field boundedly complete 396.E -field boundedly complete 396.E
 -field complete 396.E -field complete 396.E
 -field D-sufficient 396.J -field D-sufficient 396.J
 -field decision theoretically sufficient 396.J -field decision theoretically sufficient 396.J
 -field minimal sufficient 396.F -field minimal sufficient 396.F
 -field pairwise sufficient 396.F -field pairwise sufficient 396.F
 -field test sufficient 396.J -field test sufficient 396.J
 -finite (measure space) 270.D -finite (measure space) 270.D
 -function, of Weierstrass 134.F App. Table -function, of Weierstrass 134.F App. Table
 -locally finite covering (of a set) 425.R -locally finite covering (of a set) 425.R
 -process (of a complex manifold) 72.H -process (of a complex manifold) 72.H
 -space 425.Y -space 425.Y
 -subfield necessary 396.E -subfield necessary 396.E
 -subfield sufficient 396.E -subfield sufficient 396.E
 -weak topology 308.B -weak topology 308.B
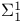 set 22.A set 22.A
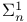 set 22.D set 22.D
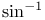 131.E 131.E
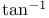 131.E 131.E
 -function 150.D -function 150.D
 (topology) 424.R (topology) 424.R
 Eddington’s App. A Table Eddington’s App. A Table
 -covering 273.B -covering 273.B
 -entropy 213.E -entropy 213.E
 -expansion 111.C -expansion 111.C
 -factor 450.N -factor 450.N
 -flat 178.D -flat 178.D
 -Hermitian form 60.O -Hermitian form 60.O
 -independent partitions 136.E -independent partitions 136.E
 -induction, axiom of 33 -induction, axiom of 33
 -neighborhood (of a point) 273.C -neighborhood (of a point) 273.C
 -number 312.C -number 312.C
 -operator, Hilbert 411.J -operator, Hilbert 411.J
 -quantifier, Hilbert 411.J -quantifier, Hilbert 411.J
 -sphere (of a point) 273.C -sphere (of a point) 273.C
 -symbol, Hilbert 411.J -symbol, Hilbert 411.J
 -tensor product 424.R -tensor product 424.R
 -theorem (in predicate logic) 411.J -theorem (in predicate logic) 411.J
 -trace form 60.O -trace form 60.O
 -subsequence 354.E -subsequence 354.E
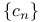 -consistency, -consistency, 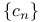 -consistent 399.K -consistent 399.K
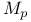 , ultradistribution of class 125.U , ultradistribution of class 125.U
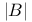 -summable series 379.O -summable series 379.O
(B,N)-pair 151.J
(DF)-space 424.P
(F)-space 424.I
(F, F’)-free (compact oriented G-manifold) 431.G
(H, p)-summable 379.M
(LF)-space 424.W
(M)-space (= Montel space) 424.O
(n + 2)-hyperspherical coordinates 79.A 90.B
(o)-convergent 87.L
(o)-star convergent 87.L
(p + 1)-stage method 303.D
(p, q)-ball knot 235.G
(p, q)-knot 235.G
(R,k)-summable 379.S
(R,S)-exact sequence (of modules) 200.K
(R,S)-injective module 200.K
(R,S)-projective module 200.K
(S)-space 424.S
* see also “Star”
*-automorphism group 36.K
*-derivation 36.K
*-homomorphism 36.F
*-representation (of a Banach *-algebra) 36.F
*-subalgebra 443.C
1-1(mapping) 381.C
1-complete manifold, weakly 21.L
2-isomorphic 186.H
3j-symbol 353.B
4-current density 150.B
4-momentum operators 258.A D
5-set 308.I
6j-symbol 353.B
9j symbol 353.C
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



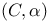 -suinmation
-suinmation 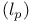 or
or 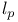 (a sequence space)
(a sequence space) 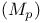 , ultradistribution of class
, ultradistribution of class 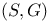 -valued random variable
-valued random variable 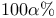 -point
-point 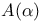 -stability
-stability 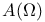 (the totality of functions bounded and continuous on the closure of
(the totality of functions bounded and continuous on the closure of  and holomorphic in
and holomorphic in 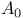 -stability
-stability 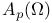 (the totality of functions
(the totality of functions 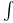 that are holomorphic in
that are holomorphic in 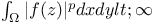
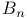 set
set  -conjugacy,
-conjugacy,  -manifold
-manifold 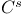 -structure)
-structure) 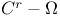 -stable
-stable 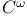 -homomorphism (between Lie groups)
-homomorphism (between Lie groups) 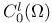 (the totality of functions in
(the totality of functions in 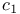 -bundle
-bundle 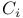 -field
-field 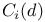 -field
-field 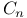 set
set 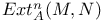
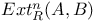
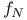 -metric
-metric 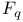 (finite field with q elements)
(finite field with q elements) 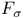 set
set 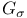 -set
-set 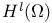 (Sobolev spaces)
(Sobolev spaces) 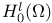 (Sobolev spaces)
(Sobolev spaces) 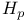 (Hardy spaces)
(Hardy spaces) 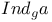
 -algebra (of a locally compact Hausdorff group)
-algebra (of a locally compact Hausdorff group)  -space, abstract
-space, abstract 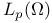 (the space of measurable functions f(x) on
(the space of measurable functions f(x) on 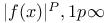 , is integrable)
, is integrable) 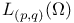 (the Lorentz spaces)
(the Lorentz spaces) 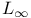
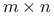 matrix
matrix 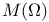 (the set of all essentially bounded measurable factions on
(the set of all essentially bounded measurable factions on 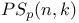 (projective symplectic group over K)
(projective symplectic group over K) 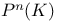 (projective space)
(projective space) 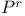 -figure
-figure 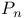 set
set 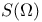 (totality of measurable functions on
(totality of measurable functions on 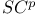 -manifold
-manifold 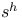 -factorial experiment
-factorial experiment 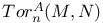
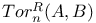
 -statistic Hotelling’s
-statistic Hotelling’s 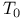 -space
-space 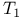 -space
-space 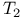 -space
-space 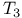 -space
-space 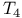 -space
-space 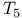 -space
-space 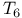 -space
-space 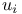 -scale
-scale 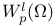 (Sobolev space)
(Sobolev space) 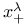 (distribution)
(distribution) 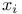 -axis (of a Euclidean space)
-axis (of a Euclidean space) 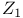 -extension
-extension  -capacity
-capacity 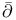 -cohomology groups
-cohomology groups 
 -equivalent (closed on G-manifolds)
-equivalent (closed on G-manifolds) 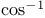
 -delta
-delta  -refinement (of a covering)
-refinement (of a covering) 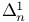 -set
-set 
 -equivalent (points)
-equivalent (points) 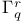 -structure
-structure 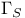 -foliation
-foliation 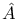 -characteristic class (of a real oriented vector bundle)
-characteristic class (of a real oriented vector bundle)  -function
-function 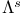 (Lipschitz spaces)
(Lipschitz spaces) 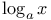
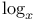
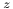 (logarithm)
(logarithm) 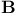 -complete (locally convex space)
-complete (locally convex space) 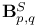 (Besov spaces)
(Besov spaces) 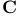 (complex numbers)
(complex numbers) 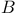 -measurable set
-measurable set 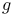 -lattice (of a separable algebra)
-lattice (of a separable algebra) 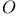 -differential (on an algebraic curve)
-differential (on an algebraic curve)  -ideal integrated two-sided
-ideal integrated two-sided 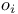 -ideal, left
-ideal, left 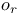 -ideal, right
-ideal, right 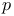 adic exponential valuation
adic exponential valuation 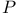 -function, Weierstrass
-function, Weierstrass 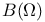
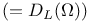
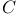 -group
-group 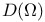
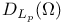 (the totality of functions f(x) in
(the totality of functions f(x) in 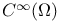 such that for all
such that for all 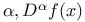 belongs to
belongs to 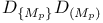
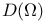
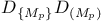
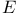 -function
-function 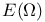
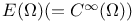
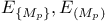
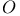 -module
-module 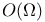 (space of holomorphic functions in
(space of holomorphic functions in 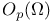
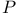 -acyclic
-acyclic 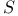 (the totality of rapidly decreasing
(the totality of rapidly decreasing 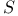 (the totality of tempered distributions)
(the totality of tempered distributions) 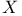 -minimal function
-minimal function  -absolutely continuous (additive set function)
-absolutely continuous (additive set function)  -connected space
-connected space 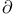 -functor
-functor 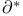 -functor
-functor  -group
-group 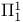 set
set 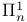 set
set  -set
-set  -space
-space  -additive measure
-additive measure 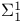 set
set 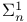 set
set 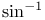
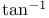
 -function
-function  (topology)
(topology)  -subsequence
-subsequence 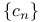 -consistency,
-consistency, 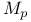 , ultradistribution of class
, ultradistribution of class 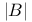 -summable series
-summable series