|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ito K. — Encyclopedic Dictionary of Mathematics. Vol. 2 |
|
|
 |
| Предметный указатель |
Axiom of parallels (in Euclidean geometry) 139.A 155.B
Axiom of reducibility (in symbolic logic) 156.B 411.K
Axiom of regularity 33.B
Axiom of replacement 33.B 381.G
Axiom of separation 33.B
Axiom of strong infinity 33.E
Axiom of subsets 33.B 381.G
Axiom of substitution 381.G
Axiom of the empty set 33.B
Axiom of the power set 33.B 381.G
Axiom of the sum set 33.B
Axiom of the unordered pair 33.B
Axiom of union 381.G
Axiom Osterwalder — Schrader 150.F
Axiom Pasch 155.B
Axiom second countability 425.P
Axiom system of 35.B
Axiom system of a structure 409.B
Axiom system of a theory 411.I
Axiom system(s) 35
Axiom the first separation 425.Q
Axiom the fourth separation 425.Q
Axiom the second separation 425.Q
Axiom the third separation 425.Q
Axiom(s) 35.A 411.I
Axiomatic quantum field theory 150.D
Axiomatic set theory 36 156.E
Axiomatization 35.A
Axiomatize (by specifying a system of axioms) 35.B
Axioms Archimedes (for real numbers) 355.B
Axioms Archimedes (in geometry) 155.B
Axioms of continuity Dedekind’s 355.A
Axioms Tietze’s first 425.Q
Axioms Tietze’s second 425.Q
Axioms Tikhonov’s separation 425.Q
Axioms Vietoris 425.Q
AxiomWightman 150.D
Axis 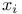 (of a Euclidean space) 140 (of a Euclidean space) 140
Axis (axes) of a circular cone 78.A
Axis conjugate (of a hyperbola) 78.C
Axis coordinate (of a Euclidean space) 140
Axis coordinate (of an affine frame) 7.C
Axis imaginary 74.C
Axis major (of an ellipse) 78.C
Axis minor (of an ellipse) 78.C
Axis of a parabola 78.C
Axis of convergence 240.B
Axis of rotation (of a surface of revolution) 111.I
Axis optical 180.B
Axis principal (of a central conic) 78.C
Axis principal (of a parabola) 78.C
Axis principal (of a quadric surface) 350.B
Axis principal, of inertia 271.E
Axis principal, transformation to 390.B
Axis real 74.C
Axis transverse (of a hyperbola) 78.C
Ayoub, Raymond George 4.r 123.r 295.r 328.r
Azencott, Robert Guy 136.G
Azima, Naonobu 230
Azimuth App. A Table
Azimuthal quantum number 315.E
Aziz, Abdul Kadir 303.r
Azra, Jean-Pierre 171.r
Azumaya algebra 29.K
Azumaya Goro 8.* r K.
Azumaya lemma, Krull- 67.D
b-function 125.EE 418.H
BA 102.L
Babbage, Charles 75.A
Bachelier, Louis 45.A
Bachet de Meziriac, Claude Gaspar 296.A
Bachmann, Paul Gustav Heinrich 297.I
Back substitution 302.B
Backward analysis 138.C
Backward difference 223.C App.
Backward emission 320.A
Backward equation, Kolmogorov 115.A 260.F
Backward error analysis 302.B
Backward interpolation formula Gauss 223.C
Backward interpolation formula Newton 223.C
Backward moving average representation 395.D
Backward moving average representation canonical 395.D
Backward type 304.D F
Bacon, Francis 401.E
Badly approximable 83.B
Baer sum (of extensions) 200.K
Baer, Reinhold 2.F 122.B 200.I K
Bagemihl, Frederick 62.C-E
Bahadur efficiency 400.K
Bahadur, Raghu Raj 396.r 398.r 399.N r r
Bahmann, H. 97.B
Bailey, Norman T. J. 40.r
Baillon, Jean-Bernard 286.Y
Baily, Walter Lewis, Jr. 16.Z 32.F H
Baiocchi, Claudio 440.r
Baire condition 425.L
Baire function 84.D
Baire measurable 270.L
Baire property 425.L
Baire property Lebesgue measurability and 33.F
Baire set 126.H 270.C
Baire space 425.L
Baire zero-dimensional space 273.B
Baire — Hausdorff theorem 273.J 425.N
Baire, Rene Louis 20 21 C L r J
Bairstow method 301.E
Bairstow, L. 301.E
Baker, Alan 118.D 182.G r r
Baker, George Allen, Jr. 142.r
Baker, Henry Frederick 9.r 15.r 78.r 350.r
Baker, Kenneth R. 376.r
Bakhshali 209
Balaban, Tadeusz 325.K
Balakrishnan, A.V. 378.D
Balanced array 102.L
Balanced fractional factorial design 102.I
Balanced incomplete 102.E
Balanced incomplete block design 102.E
Balanced incomplete block design partially 102.J
Balanced incomplete efficiency-balanced 102.E
Balanced incomplete optimal 102.E
Balanced incomplete randomized 102.B
Balanced incomplete variance-balanced 102.E
Balanced mapping, A- 277.J
Balas, Egon 215.C r
Balayage 338.L
Balayage principle 338.L
Baldwin, John T. 276.F
Balian, Roger 386.r
Ball 140
Ball knot, (p,q)- 235.G
Ball n- 140
Ball open 140
Ball open n- 140
Ball pair 235.G
Ball spin 351.L
Ball unit 140
Ball unit (of a Banach space) 37.B
Ball, W. W. Rouse 157.r
BAN (best asymptotically normal) 399.K
Banach (extension) theorem, Hahn- (in a normed space) 37.F
Banach (extension) theorem, Hahn- (in a topological linear space) 424.C
Banach algebra(s) 36.A
Banach analytic space 23.G
Banach area (of a surface) 246.G
Banach integral 310.I
Banach lattice 310.F
Banach Lie group 286.K
Banach limit 37.F
Banach manifold 105.Z
| Banach space reflexive 37.G
Banach space regular 37.G
Banach space(s) 37.A B
Banach star algebra 36.F
Banach theorem 37.I
Banach — Alaoglu theorem (in a Banach space) 37.E
Banach — Alaoglu theorem (in a topological linear space) 424.H
Banach — Steinhaus theorem (in a Banach space) 37.H
Banach — Steinhaus theorem (in a topological linear space) 424.J
Banach, Stefan 20 23.G 36.A F B E F H I O r Z I H J X
Band, Mobius 410.B
Banerjee, Kali S. 102.r
Bang, Thoger Sophus Vilhelm 58.F
Bang-bang control 405.C
Banica (Banica), Constantin 23.r
Baouendi, M. Salah 323.N 345.A
Bar construction (of an Eilenberg — MacLane complex) 70.F
Bar-Hillel, Yehoshua 96.r
Barankin theorem 399.D
Barankin, Edward William 396.r 399.D r
Barban, Mark Borisovich 123.E
Barbey, Klaus 164.r
Barbosa, Joao Lucas Marques 275.B
Barbu, Viorel 88.r 440.r
Barden, Dennis 65.C
Bardos, Claude Williams 204.E
Bargaining set 173.D
Bargaining solution, Nash 173.C
Bargmann, Valentine 258.r 437.EE
Bari, Nina Karlovna 159.J
Barlow, Peter NTR
Barlow, William 92.F
Barnes extended hypergeometric function 206.C App. Table
Barnes, Ernest William 206.C App. A Table
Barr, Michael 200.r
Barrel (in a locally convex space) 424.I
Barreled (locally convex space) 424.I
Barreled (locally convex space)quasi- 424.I
Barrier 120.D
Barrier absorbing 115.B
Barrier reflecting 15.B C
Barrow, Isaac 265 283
Barth, Wolf Paul 16.r
Bartle — Dunford — Schwartz integral 443.G
Bartle, Robert Gardner 68.M 443.A G
Bartlett, Maurice Stevenson 40.r 44.r 280.J 407.r421.C r
Barwise, Jon 356.r
Barycenter (of a rigid body) 271.E
Barycenter (of points of an affine space) 7.C
Barycentric coordinates (in a Euclidean complex) 70.B
Barycentric coordinates (in an affine space) 7.C 90.B
Barycentric coordinates (in the polyhedron of a simplicial complex) 70.C
Barycentric derived neighborhood, second 65.C
Barycentric refinement 425.R
Barycentric subdivision (of a Euclidean complex) 70.B
Barycentric subdivision (of a simplicial complex) 70.C
Baryons 132.B
Base (curve of a roulette) 93.H
Base (in a Banach space) 37.L
Base (of a logarithmic function) 131.B
Base (of a point range) 343.B
Base (of a polymatroid) 66.F G
Base data 96.B
Base filter 87.I
Base for the neighborhood system 425.E
Base for the space 425.E
Base for the topology 425.F
Base for the uniformity 436.B
Base functions 304.B
Base local 425.E
Base normal 172.E
Base open 425.F
Base point of a linear system 16.N
Base point of a loop 170
Base point of a topological space 202.B
Base space of a fiber bundle 147.B
Base space of a fiber space 148.B
Base space of a Riemann surface 367.A
Base term (of a spectral sequence) 200.J
Base units 414.A
Bashforth method, Adams- 303.E
Bashforth, F. 303.E
Basic 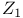 -extension 14.L -extension 14.L
Basic components (of an m-dimensional surface) 110.A
Basic concept (of a structure) 409.B
Basic equation 320.E
Basic feasible solution 255.A
Basic field (of linear space) 256.A
Basic form 255.A
Basic interval 4.B
Basic invariant 226.B
Basic limit theorem 260.C
Basic open set 425.F
Basic optimal solution 255.A
Basic property (of a structure) 409.B
Basic ring (of a module) 277.D
Basic set (for an Axiom A flow) 126.J
Basic set (of a structure) 409.B
Basic solution 255.A
Basic solution feasible 255.A
Basic solution optimal 255.A
Basic space (of a probability space) 342.B
Basic surface (of a covering surface) 367.B
Basic variable 255.A
Basic vector field 80.H
Basin 126.F
Basis (in a Banach space) 37.L
Basis (of a homogeneous lattice) 182.B
Basis (of a linear space) 256.E
Basis (of a module) 277.G
Basis (of an Abelian group) 2.B
Basis (of an ideal) 67.B
Basis canonical 201.B
Basis canonical homology 11.C
Basis Chevailey canonical 248.Q
Basis dual 256.G
Basis minimal 14.B
Basis normal 172.E
Basis of order r in N 4.A
Basis orthonormal 197.C
Basis Schauder 37.L
Basis strongly distinguished 418.F
Basis theorem Hilbert (on Noetherian rings) 284.A
Basis theorem Ritt (on differential polynomials) 113
Basis transcendence 149.K
Basis Weyl canonical 248.P
Bass, Hyman 122.F 200.r 237 J r
Bass, Robert Wauchope 289.D
Bastin, J. 351.r
Batchelder, Paul M. 104.r
Batchelor, George Keith 205.r 433.C r
Bateman, Paul Trevier 4.D 348.K
Bath, heat 419.B
Bauer, Friedrich Ludwig 302.r
Bauer, Heinz 193.U
Baum, Paul Frank 366.E 427.B
Bayer, Pilar 450.r
Bayes estimator 399.G
Bayes formula 342.F 405.I
Bayes risk 398.B
Bayes solution 398.B
Bayes solution generalized 398.B
Bayes solution in the wider sense 398.B
Bayes sufficient cr-field 396.J
Bayes, Thomas 342.A F E
Bayesian approach 401.B
Bayesian model 403.G
Bazilevich, Ivan Evgen’evich 438.B
BCH (Base — Chaudhuri — Hooquenghem) code 63.D
BDH (Brown — Douglas — Fillmore) theory 36.J 390.J
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



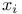 (of a Euclidean space)
(of a Euclidean space) 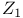 -extension
-extension