|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Munkres J. — Topology |
|
|
 |
| Предметный указатель |
 119 119
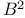 135 (see also “ 135 (see also “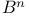 ”) ”)
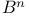 156 156
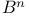 , compactness 174 , compactness 174
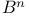 , fundamental group 331 , fundamental group 331
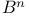 , path connectedness 156 , path connectedness 156
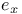 (constant path) 327 (constant path) 327
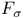 set 252 set 252
 set 194 249 set 194 249
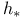 333 333
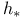 , dependence on base point 335 , dependence on base point 335
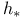 , functorial properties 334 , functorial properties 334
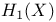 (see “First homology group”) (see “First homology group”)
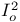 (see “Ordered square”) (see “Ordered square”)
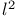 -topology 128 -topology 128
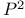 372 372
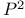 is surface 372 is surface 372
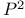 , fundamental group 373 , fundamental group 373
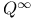 195 195
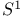 106 106
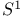 , covering spaces 337 482 , covering spaces 337 482
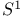 , fundamental group 345 , fundamental group 345
 139 139
 as quotient space 136 139 as quotient space 136 139
 (unit sphere) 156 (unit sphere) 156
 (unit sphere), compactness 174 (unit sphere), compactness 174
 (unit sphere), fundamental group 369 (unit sphere), fundamental group 369
 (unit sphere), path connectedness 156 (unit sphere), path connectedness 156
 (unit sphere), simple connectedness 369 (unit sphere), simple connectedness 369
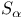 (section of well-ordered set) 66 (section of well-ordered set) 66
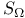 66 66
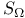 , compactification 242 , compactification 242
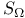 , countable subsets 66 74 , countable subsets 66 74
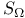 , existence 74 , existence 74
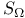 , metrizability 181 , metrizability 181
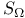 , paracompactness 260 261 , paracompactness 260 261
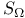 , uniqueness 73 , uniqueness 73
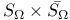 203 203
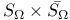 , complete regularity 212 , complete regularity 212
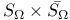 , normality 203 , normality 203
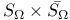 , paracompactness 254 , paracompactness 254
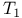 axiom 99 axiom 99
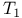 axiom for quotient space 141 axiom for quotient space 141
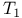 axiom vs. Hausdorff condition 99 axiom vs. Hausdorff condition 99
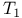 axiom vs. limit points 99 axiom vs. limit points 99
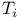 axioms 211 213 axioms 211 213
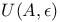 111 111
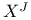 113 113
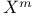 38 38
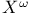 38 38
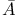 (closure) 95 (closure) 95
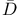 121 121
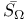 66 66
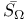 , metrizability 181 , metrizability 181
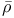 124 266 124 266
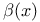 (see “Stone — (see “Stone — 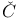 ech compactification”) ech compactification”)
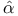 331 331
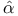 independence of path 335 independence of path 335
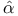 is isomorphism 332 is isomorphism 332
 (reals) 30 (reals) 30
 (reals), algebraic properties 30 (reals), algebraic properties 30
 (reals), compact subspaces 173 (reals), compact subspaces 173
 (reals), connected subspaces 154 (reals), connected subspaces 154
 (reals), K-topology 82 (see also “ (reals), K-topology 82 (see also “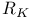 ”) ”)
 (reals), local compactness 182 (reals), local compactness 182
 (reals), lower limit topology 82 (see also “ (reals), lower limit topology 82 (see also “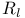 ”) ”)
 (reals), metric for 120 (reals), metric for 120
 (reals), order properties 31 (reals), order properties 31
 (reals), second-countability 190 (reals), second-countability 190
 (reals), standard topology 81 (reals), standard topology 81
 (reals), uncountability 177 (reals), uncountability 177
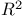 , standard topology 87 , standard topology 87
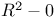 325 325
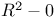 , covering space 340 , covering space 340
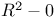 , fundamental group 360 , fundamental group 360
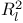 193 193
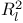 , complete regularity 212 , complete regularity 212
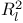 , Lindeloef condition 193 , Lindeloef condition 193
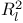 , paracompactness 257 , paracompactness 257
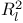 , separation axioms 198 , separation axioms 198
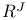 in box topology is Baire 300 in box topology is Baire 300
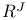 in box topology, complete regularity 213 in box topology, complete regularity 213
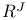 in product topology (cont.) normality 203 in product topology (cont.) normality 203
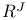 in product topology (cont.) paracompactness 257 in product topology (cont.) paracompactness 257
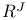 in product topology countable dense subset 195 in product topology countable dense subset 195
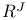 in product topology is Baire 300 in product topology is Baire 300
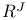 in product topology metrizability 133 in product topology metrizability 133
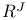 in uniform topology 124 in uniform topology 124
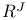 in uniform topology completeness 267 in uniform topology completeness 267
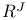 in uniform topology is Baire 300 in uniform topology is Baire 300
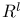 , countable dense subset 195 , countable dense subset 195
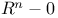 156 156
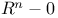 , fundamental group 360 , fundamental group 360
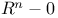 , path connectedness 156 , path connectedness 156
 38 38
 , basis 116 , basis 116
 , compact subspaces 173 , compact subspaces 173
 , local compactness 182 , local compactness 182
 , metrics for 122 123 , metrics for 122 123
 , paracompactness 253 , paracompactness 253
 , second-countability 190 , second-countability 190
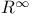 118 118
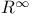 , closure in , closure in  118 127 118 127
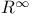 , paracompactness 260 , paracompactness 260
 38 38
 in box topology, components 162 in box topology, components 162
 in box topology, connectedness 151 in box topology, connectedness 151
 in box topology, metrizability 132 in box topology, metrizability 132
 in box topology, normality 205 in box topology, normality 205
 in box topology, paracompactness 205 in box topology, paracompactness 205
 in product topology, completeness 265 in product topology, completeness 265
 in product topology, connectedness 151 in product topology, connectedness 151
 in product topology, local compactness 182 in product topology, local compactness 182
 in product topology, metrizability 125 in product topology, metrizability 125
 in product topology, paracompactness 257 in product topology, paracompactness 257
 in product topology, second-countability 190 in product topology, second-countability 190
 in uniform topology, components 162 in uniform topology, components 162
 in uniform topology, paracompactness 257 in uniform topology, paracompactness 257
 in uniform topology, second-countability 190 in uniform topology, second-countability 190
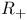 31 31
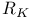 82 82
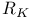 , connectedness 178 , connectedness 178
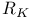 , separation axioms 197 , separation axioms 197
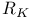 , vs. standard topology 82 , vs. standard topology 82
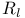 82 82
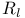 , countability axioms 192 , countability axioms 192
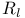 , metrizability 194 , metrizability 194
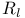 , normality 198 , normality 198
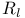 , paracompactness 257 , paracompactness 257
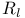 , vs. standard topology 82 , vs. standard topology 82
 32 32
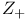 32 32
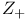 , not finite 42 , not finite 42
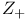 , well-ordered 32 , well-ordered 32
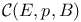 487 (see also “Group of covering transformations”) 487 (see also “Group of covering transformations”)
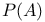 12 12
 -tuple 38 -tuple 38
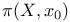 331 (see also “Fundamental group”) 331 (see also “Fundamental group”)
 122 268 122 268
 -compact 289 316 -compact 289 316
 -locally discrete 252 -locally discrete 252
 -locally finite 245 -locally finite 245
2-cell 441
2-manifold 225
2-manifold with boundary 476
2-manifold, topological dimension 308 352
2-sphere 139 (see also “ ”) ”)
Absolute retract 223
Absolute retract vs. universal extension property 223 224
Accumulation point of a net 188
| Action of a group on a space 199
Adjoining a 2-cell 441
Adjoining a 2-cell, effect on fundamental group 439
Adjunction space 224
Affinely independent 309
Alexander homed sphere 393
Algebraic number 51
Antipodal map 372
Antipode 356
Antipode-preserving 356
ARC 308 379
Arc does not separate  389 389
Archimedean ordering 33
Arzela’s theorem 280 293
Ascoli’s Theorem 278 290
Axiom of Choice 59
Axiom of choice vs. nonemptiness of product 118
Axiom of choice vs. well-ordering theorem 73
Axiom of choice, finite 61
Baire category theorem 296
Baire category theorem, special case 178
Baire space 295
Baire space (cont.), 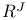 in box, product, uniform topologies 300 in box, product, uniform topologies 300
Baire space (cont.), open subspace of Baire space 297
Baire space, compact Hausdorff space 296
Baire space, complete metric space 296
Baire space, fine topology on 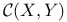 300 300
Baire space, locally compact Hausdorff space 299
Ball, unit 135 156
Barber of Seville paradox 47
Base point 331
Base point choice, effect on 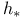 335 335
Base point choice, effect on 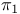 332 332
Basis for a free abelian group 411
Basis for a topology 78 80
Basis for box topology 115 116
Bd A 102
Betti number 424
Bicompactness 178
Bijective function 18
Binary operation 30
Bing metrization theorem 252
Bisection theorem 358 359
Borsuk lemma 382 385
Borsuk — Ulam theorem 358 359
Boundary of a set 102
Boundary of a surface with boundary 476
Bounded above 27
Bounded below 27
Bounded function 267
Bounded metric 121 129
Bounded set 121
Box topology 114
Box topology vs. fine topology 290
Box topology vs. product topology 115
Box topology vs. uniform topology 124 289 290
Box topology, Hausdorff condition 116
Box topology, subspace 116
Brouwer fixed-point theorem 351 353
Cantor set 178
Cardinality of a finite set 39 42
Cardinality, comparability 68
Cardinality, greater 62
Cardinality, same 51
Cartesian product, countably infinite 38
Cartesian product, finite 13 37
Cartesian product, general 113
Cauchy integral formula 405
Cauchy sequence 264
Choice axiom (see “Axiom of choice”)
Choice function 59
Circle, unit (see “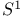 ”) ”)
Classification of covering spaces 482
Classification of covering transformations 488
Classification of surfaces 469
Clockwise loop 405
Closed edge path 566
Closed graph theorem 171
Closed interval 84
Closed map 137
Closed ray 86
Closed refinement 245
Closed set 93
Closed set in subspace 94
Closed set vs. limit points 98
Closed topologist’s sine curve 381
Closed topologist’s sine curve, separates  381 393 381 393
Closure 95
Closure (cont.) via limit points 97
Closure (cont.) via sequences 130 190
Closure in a cartesian product 101 116
Closure in a subspace 95
Closure of a connected subspace 150
Closure of a union 101 245
Closure via basis elements 96
Closure via nets 187
Coarser topology 77
Cofinal 187
Coherent topology 224 435
Collection 12
Commutator 422
Commutator subgroup 422
Compact 164 (see also “Compact Hausdorff space”; “Compactness”)
Compact convergence topology 283
Compact convergence topology vs. compact-open topology 285
Compact convergence topology vs. pointwise convergence topology 285
Compact convergence topology vs. uniform topology 285
Compact convergence topology, independence of metric 286
Compact Hausdorff space is Baire space 296
Compact Hausdorff space, components equal quasicomponents 236
Compact Hausdorff space, metrizability 218
Compact Hausdorff space, normality 202
Compact Hausdorff space, paracompactness 252
Compact-open topology 285
Compact-open topology continuity of evaluation map 286
Compact-open topology vs. compact convergence topology 285
Compactification 185 237
Compactification of (0, 1) 238
Compactification, induced by an imbedding 238
Compactification, one-point 185
Compactly generated space 283
Compactness 164 (see also “Compact Hausdorff space”)
Compactness and least upper bound property 172
Compactness and perfect maps 172
Compactness closed set criterion 169
Compactness in  and and  173 173
Compactness in 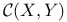 290 293 290 293
Compactness in 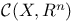 278 279 278 279
Compactness in finite complement topology 166
Compactness in Hausdorff metric 281
Compactness in order topology 172
Compactness of closed intervals in M 173
Compactness of continuous image 166
Compactness of countable products 280
Compactness of finite products 167
Compactness of product space 234 236
Compactness of subspace 164
Compactness via nets 188
Compactness vs. completeness 276
Compactness vs. limit point compactness 179
Compactness vs. sequential compactness 179
Comparability of cardinalities 68
Comparability of topologies 77
Comparability of well-ordered sets 73
Comparison test for infinite series 135
Complement 10
Complete graph 394
Complete graph on five vertices 308 397
Complete metric space 264 (see also “Completeness”)
Complete regularity 211
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



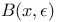
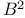
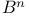 ”)
”)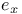 (constant path)
(constant path) 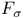 set
set  set
set 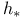
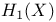
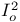
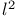 -topology
-topology 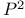
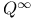
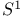

 (unit sphere)
(unit sphere) 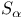 (section of well-ordered set)
(section of well-ordered set) 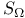
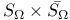
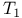 axiom
axiom 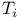 axioms
axioms 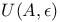
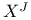
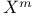
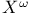
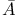 (closure)
(closure) 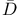
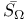
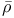
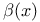
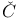 ech compactification”)
ech compactification”)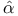
 (reals)
(reals) 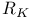 ”)
”)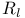 ”)
”)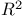 , standard topology
, standard topology 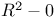
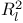
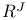 in box topology is Baire
in box topology is Baire 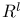 , countable dense subset
, countable dense subset 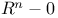

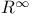

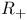

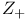
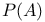
 -tuple
-tuple 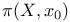

 -compact
-compact