|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Munkres J. — Topology |
|
|
 |
| Предметный указатель |
Frobenius theorem 351
Function 16
functor 242
Functorial properties of 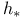 3 34 3 34
Fundamental group 371
Fundamental group of 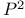 373 373
Fundamental group of 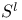 345 345
Fundamental group of  369 369
Fundamental group of 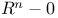 360 360
Fundamental group of a product 371
Fundamental group of deformation retract 361
Fundamental group of double torus 374 452
Fundamental group of dunce cap 444
Fundamental group of figure eight 362 373
Fundamental group of infinite earring 500
Fundamental group of linear graph 511
Fundamental group of m-fold projective plane 453
Fundamental group of n-fold torus 452
Fundamental group of theta space 362 432
Fundamental group of torus 371 442
Fundamental group of wedge of circles 434 436
Fundamental group of wedge of spaces 438
Fundamental group, when abelian 335
Fundamental group, when countable 499 500
Fundamental group, when finitely generated 500
Fundamental group, when uncountable 500
Fundamental theorem of algebra 354
G/H 146 331
G/H as topological group 146
G/H, regularity 146
General lifting lemma 478
General linear group 146
General nonseparation theorem 390
General position 308 310
General separation theorem 380 392
Generalized Continuum Hypothesis 62
Generated by elements 411 421.
Generated by subgroups 407 412
Generator of cyclic group 346
Geometrically independent 309
Graph of a function 171
Greater cardinality 62
Greatest lower bound 27
Greatest lower bound, property 27
Group of covering transformations 487
Groupoid properties 326
Hahn — Mazurkiewicz Theorem 275
Half-open interval 84
Ham sandwich theorem 359
Hausdorff condition 98
Hausdorff condition and closedness of diagonal 100
Hausdorff condition and convergent sequences 99
Hausdorff condition and perfect maps 199
Hausdorff condition and uniqueness of extensions 112 240
Hausdorff condition for box topology 116
Hausdorff condition for manifold 227
Hausdorff condition for metric space 129
Hausdorff condition for orbit space 199
Hausdorff condition for order topology 100
Hausdorff condition for product space 100 116 196
Hausdorff condition for quotient space 142
Hausdorff condition for subspace 100 196
Hausdorff condition for topological group 146
Hausdorff condition vs. 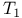 axiom 99 axiom 99
Hausdorff condition vs. regularity 195 197
Hausdorff condition, normality 202
Hausdorff condition, paracompactness 257
Hausdorff condition, subspace 129
Hausdorff maximum principle 69
Hausdorff metric 281
Hausdorff space 98 (see also “Hausdorff condition”)
Have the same cardinality 51
Hilbert cube 128
Homeomorphism 105
Homeomorphism vs. continuous bijective map 106 167
Homogeneous space 146
Homology group 455
Homomorphism 330
Homomorphism, induced by a map 333 (see also ht)
Homomorphism, induced by a path 331 (see also a)
Homotopic maps 323
Homotopy 323
Homotopy as path in function space 288
Homotopy equivalence 363
Homotopy equivalence vs. deformation retraction 365 366
Homotopy equivalence, induces isomorphism of 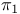 364 364
Homotopy extension lemma 381
Homotopy inverse 363
Homotopy type 363
Homotopy type of contractible space 366
Homotopy, effect on 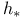 360 363 364 360 363 364
Homotopy, straight-line 325
Hypothesis 7
Identification space 139
Identity function 21
Image 16 19
Imbedding 105
Imbedding theorem for a compact manifold 226 314
Imbedding theorem for a completely regular space 217
Imbedding theorem for a linear graph 308
Imbedding theorem for a manifold 316
Imbedding theorem for a space of dimension m 311
Imbedding, isometric 133
Immediate predecessor 25
Immediate successor 25
inclusion 4
Index of a subgroup 514
Index set 36
Indexed family of sets 36
Indexing function 36
Indiscrete topology 77
Induction principle 32
Induction principle, strong 33
Induction principle, transfinite 67
Inductive definition 47 (see also “Recursive definition”)
Inductive dimension 315
Inductive set 32 67
Inf A 27
Infimum 27
Infinite broom 162
Infinite earring 436
Infinite earring, fundamental group 500
Infinite earring, no universal covering 487
Infinite sequence 38
Infinite series 135
Infinite set 44
Infinite set via injective and bijective functions 57
Initial point of a path 323
Initial point of an oriented line segment 447 506
Injective function 18
Int A 95
Integers 32
Interior point of a set 95
Interior point of an arc 379
Intermediate-value theorem 147 154
Intersection 6 12 36
interval 25 84
Intervals in  compactness 173 compactness 173
Intervals in  connectedness 154 connectedness 154
Intervals in  topological dimension 305 topological dimension 305
Invariance of domain 383 385
Inverse function 18
Inverse image 19
Isolated point 176
Isometric imbedding 133
Isometric imbedding in complete metric space 269 271
Isometry 181
Isomorphism 105 330
J-tuple 113
Jordan curve theorem 390
| Jordan separation theorem 379
K-fold covering 341
K-plane 310
K-topology on  82 (see also 82 (see also 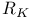 ) )
Kernel of homomorphism 330
Klein bottle 454
Kuratowski 14-set problem 102
Kuratowski lemma 72
Labelling 447
Labelling scheme 449 (see also “Scheme”)
labels 447
Larger topology 77
largest element 27
Least normal subgroup 419
Least normal subgroup, generators 420
Least upper bound 27
Least upper bound property 27
Least upper bound property and compactness 172 177
Least upper bound property and local compactness 183
Least upper bound property for  31 31
Least upper bound property for well-ordered sets 66
Least upper bound property vs. greatest lower bound property 29
Lebesgue number 175
Lebesgue number lemma 175
Left coset 146 330
Left inverse 21
Length of a word 412
Lens space 494
Lifting 342
Lifting correspondence 345
Lifting lemma for path homotopies 343
Lifting lemma for paths 342
Lifting lemma, general 478
Limit of a sequence 100
Limit point 97
Limit point compactness 178
Limit point compactness vs. compactness 179
Limit point compactness vs. countable compactness 181
Limit point vs. 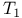 axiom 99 axiom 99
Lindeloef condition 192 (see also “Regular Lindeloef space”)
Lindeloef condition for 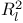 193 193
Lindeloef condition for 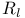 192 192
Lindeloef condition for closed subspace 194
Lindeloef condition for products 193
Lindeloef condition for subspace 193
Lindeloef condition, effect of continuous function 194
Line with two origins 227
Linear continuum 31 153
Linear continuum, compact subspaces 172
Linear continuum, connected subspaces 153
Linear continuum, long line 158
Linear continuum, normality 206
Linear continuum, ordered square 155
Linear graph 308 394 502
Linear graph, fundamental group 511
Linear graph, imbedding in 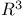 308 308
Linear graph, local path connectedness 504
Linear graph, local simple connectedness 504
Linear graph, semilocal simple connectedness 504
Linear graph, topological dimension 308
Linear order 24
Little ell-two topology 128
Local compactness 182
Local compactness and least upper bound property 183
Local compactness and perfect maps 199
Local compactness for orbit space 199
Local compactness of  and and  and and  182 182
Local compactness of products 186
Local compactness of subspace 185
Local compactness, implies compactly generated 283
Local connectedness 161
Local connectedness of quotient space 163
Local connectedness vs. weak local connectedness 162
Local homeomorphism 338
Local metrizability 218 261
Local path connectedness 161
Local simple connectedness 495
Local simple connectedness vs. simple connectedness 499
Locally compact Hausdorff space, Baire condition 299
Locally compact Hausdorff space, complete regularity 213
Locally compact Hausdorff space, regularity 205
Locally discrete 254
Locally Euclidean 316
Locally finite collection 244
Locally finite family 112
Locally finite family vs. locally finite collection 245
Logical equivalence 8
Logical quantifiers 9
Long line 158 317
Long line, connectedness 159
Long line, path connectedness 159
Loop 331
Lower bound 27
Lower limit topology 82 (see also  ) )
M-fold projective plane 452
M-fold projective plane, first homology group 456
M-fold projective plane, fundamental group 453
m-tuple 37
Manifold 225 316
Manifold, imbedding in  226 314 316 226 314 316
Manifold, metrizability 227
Manifold, necessity of Hausdorff condition 227
Manifold, regularity 227
Manifold, topological dimension 314 316
Mapping 16
Maximal element 70
Maximal tree 509
Maximum principle 69
Maximum principle vs. well-ordering theorem 73
Maximum principle vs. Zorn’s lemma 70 72
Maximum value theorem of calculus 147
Maximum value theorem, general 174
Metric 119
Metric for  120 120
Metric for  122 122
Metric for  125 125
Metric for Discrete topology 120
Metric space 120
Metric topology 119
Metric, bounded 129
Metrically equivalent 270
Metrizability of 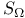 and and 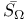 181 181
Metrizability of 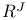 133 133
Metrizability of  123 123
Metrizability of  125 132 125 132
Metrizability of 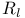 194 194
Metrizability of compact Hausdorff space 218
Metrizability of manifolds 227
Metrizability of ordered square 194
Metrizability of products 133 134
Metrizability of regular Lindelof space 218
Metrizability of regular second-countable space 215
Metrizability of Stone-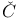 ech compactification 242 ech compactification 242
Metrizable space 120
Minimal uncountable well-ordered set 66 (see also “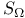 ”) ”)
Moebius band 450
Monomorphism 330
N(f, a) (see “Winding number”)
N-fold torus 451
N-fold torus, first homology group 456
N-fold torus, fundamental group 452
Nagata — Smimov metrization theorem 250
Negation 9
Neighborhood 96
Nested sequence of sets 170
Net 187
No-retraction theorem 348
Nonseparation theorem, arc in  389 389
Nonseparation theorem, general 390
Nonseparation theorem, topologist’s sine curve in  393 393
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



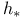
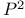
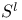

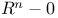
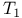 axiom
axiom 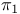
 compactness
compactness 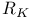 )
)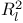
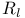
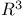
 and
and 
 )
)
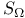 and
and 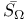
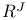
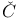 ech compactification
ech compactification 