|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Munkres J. — Topology |
|
|
 |
| Предметный указатель |
Sorgenfrey plane 193 (see also “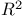 ”) ”)
Sphere, unit 139 156 “
Square metric 122 (see also “ ”) ”)
Standard bounded metric 121
Standard topology, on  81 81
Standard topology, on 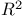 87 87
Star-convex set 334
Stereographic projection 369
Stone-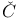 ech compactification 241 ech compactification 241
Stone-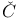 ech compactification of ech compactification of 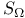 242 242
Stone-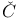 ech compactification of ech compactification of 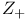 242 242
Stone-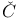 ech compactification, existence 239 ech compactification, existence 239
Stone-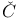 ech compactification, extension condition 240 ech compactification, extension condition 240
Stone-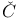 ech compactification, metrizability 242 ech compactification, metrizability 242
Stone-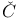 ech compactification, uniqueness 240 ech compactification, uniqueness 240
Straight-line homotopy 325
Strict partial order 68
Strictly coarser topology 77
Strictly finer topology 77
Strong continuity 137
Strong induction principle 33
Stronger topology 78
Subbasis 82
Subbasis for order topology 86
Subbasis for product topology 88 114
Subgraph 503
Subgroup of free abelian group 412
Subgroup of free group 514
Subnet 188
Subsequence 179
Subset 4
Subspace topology 88
Subspace topology in metric space 129
Subspace topology vs. box topology 116
Subspace topology vs. order topology 91
Subspace topology vs. product topology 89 116
Subspace topology, basis 89
Subspace topology, compactness 164
Subspace topology, complete regularity 211
Subspace topology, connectedness 148
Subspace topology, countable dense subset 194
Subspace topology, first-countability 191
Subspace topology, Hausdorff condition 100 196
Subspace topology, Lindeloef condition 193 194
Subspace topology, local compactness 185
Subspace topology, normality 203 205
Subspace topology, paracompactness 254
Subspace topology, regularity 196
Subspace topology, second-countability 191
Subspace topology, topological dimension 306
Sum of groups 407
Sup A 27
Sup metric 268
Sup metric vs. uniform metric 268
Superset 233
Support 225 257
Supremum 27
surface 225 370
Surface with boundary 476
Surface, classification 457
Surjective function 18
Symmetric neighborhood 146
System of free generators 421
Theta space 362 394
Theta space, fundamental group 432
Theta space, separates  395 395
Tietze extension theorem 219
Topological completeness 270 (see also “Complete metric space”)
Topological dimension 305
Topological dimension of 1 -manifold 308
Topological dimension of 2-manifold 308 352
Topological dimension of a union 307 308
Topological dimension of closed subspace 306
Topological dimension of closed subspace of 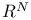 316 316
Topological dimension of compact manifold 314
Topological dimension of compact subspace of  305 305
Topological dimension of compact subspace of 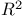 306 306
Topological dimension of compact subspace of 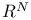 313 313
Topological dimension of linear graph 308
Topological dimension of manifold 316
Topological dimension of triangular region 352
Topological dimension of [0, 1] 305
Topological group 145
Topological group, 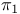 is abelian 335 is abelian 335
Topological group, closedness of 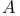 172 188 172 188
Topological group, complete regularity 213
Topological group, covering space of 483
Topological group, Hausdorff condition 146
Topological group, normality 207
Topological group, paracompactness 261
Topological group, regularity 146
Topological group, second-countability 195
Topological imbedding 105
Topological property 105
Topological space 76
Topologist's sine curve 157
Topologist's sine curve, components 160
Topologist’s sine curve (cont.), connectedness 156
Topologist’s sine curve (cont.), does not separate  393 393
Topologist’s sine curve (cont.), path components 160
Topologist’s sine curve (cont.), path connectedness 157
topology 76
Topology, generated by a basis 78 80
Topology, generated by a subbasis 82
Torsion subgroup 412 424
Torus 339
| Torus as quotient space 136 140
Torus, equals doughnut surface 339
Torus, fundamental group 371 442
Torus-type scheme 463
Totally bounded 275
Totally bounded vs. equicontinuity 277
Totally disconnected 152
Tower 73
Transcendental number 51
Transfinite induction 67
Translation of 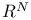 310 310
TREE 507
Tree, fundamental group 508
Tree, maximal 509
Triangle inequality 119
Triangulable 471
Triangulation 471
Trivial homomorphism 335
Trivial topology 77
Tube 167
Tube lemma 168
Tube lemma, generalized 171
Tukey lemma 72
Tychonoff theorem 234
Tychonoff theorem for countable products 280
Tychonoff theorem for finite products 167
Tychonoff theorem via well-ordering theorem 236
Uncountability of 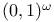 49 49
Uncountability of  177 177
Uncountability of  50 50
Uncountability of transcendental numbers 51
Uncountable set 45
Uncountable well-ordered set 74 (see also “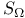 ”) ”)
Uniform boundedness principle 299
Uniform continuity theorem 147 176
Uniform convergence 131
Uniform convergence on compact sets 283
Uniform convergence, Weierstrass M-test for 135
Uniform limit theorem 132
Uniform limit theorem, converse fails 134
Uniform limit theorem, partial converse 171
Uniform metric 124 266
Uniform metric vs. sup metric 268
Uniform metric, completeness 267
Uniform structure 292
Uniform topology 124 266
Uniform topology vs. box topology 124
Uniform topology vs. compact convergence topology 285
Uniformly continuous 176
union 5 12 36
Unit ball 135 331 “
Unit circle 106 (see also “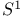 ”) ”)
Unit sphere 156 (see also “ ”) ”)
Universal covering space 484
Universal covering space, existence 498
Universal extension property 223
Upper bound 27 70
Urysohn lemma 207
Urysohn lemma, strong form 213
Urysohn Metrization Theorem 215
Utilities graph 308 394
Utilities graph, nonembeddability 396
Vacuously true 7
Value of a function 16
Vanish at infinity 280
Vanish precisely on A 213
Vector field 350
Vertex of a curved triangle 471
Vertex of a linear graph 308 394 502
Vertex of a polygonal region 447
Weak local connectedness 162
Weak local connectedness vs. connectedness 162
Weaker topology 78
Wedge of circles 434 435
Wedge of circles, existence 437
Wedge of circles, fundamental group 434 436
Wedge of spaces 438
Weierstrass M-test 135
Well-ordered set 63
Well-ordered set, 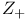 32 32
Well-ordered set,  63 63
Well-ordered set, compact subspaces 172
Well-ordered set, dictionary order 64
Well-ordered set, finite 64
Well-ordered set, normality 202
Well-ordered set, subsets well-ordered 63
Well-ordered set, uncountable 66
Well-ordering theorem 65
Well-ordering theorem and axiom of choice 67 73
Well-ordering theorem and maximum principle 70 73
Well-ordering theorem, applied 236 246
Winding number 398 403
Winding number as an integral 405
Winding number of simple closed curve 404 406
Word 412 415
Word, reduced 413
Zermelo 65
Zorn’s Lemma 70
Zorn’s lemma vs. maximum principle 75
Zorn’s lemma, applied 72 233 236 509
[f] 324
[G, G] 422
[x, y] 330
“If... then,” meaning of 7
“Onto” function 18
“Or,” meaning of 5
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



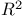 ”)
”) ”)
”)
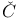 ech compactification
ech compactification 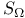
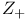

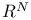
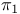 is abelian
is abelian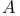
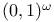

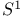 ”)
”) ”)
”)