|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Munkres J. — Topology |
|
|
 |
| Предметный указатель |
Norm 122
Normal space 195 (see also “Normality”)
Normal subgroup 330
Normality 195
Normality of 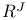 203 203
Normality of 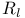 198 198
Normality of adjunction space 224
Normality of closed subspace 205
Normality of coherent topology 224
Normality of compact Hausdorff space 202
Normality of linear continuum 206
Normality of linear graph 502
Normality of metric space 202
Normality of orbit space 199
Normality of paracompact Hausdorff space 253
Normality of product 198 203
Normality of quotient space 199 443
Normality of regular Lindeloff space 205
Normality of regular second-countable space 200
Normality of subspace 203
Normality of topological group 207
Normality of well-ordered set 202
Normality vs. complete regularity 211 212
Normality vs. regularity 195 198 203
normalizer 487
Nowhere-differentiable function 300
Nulhomotopic map 323
Nulhomotopic map, induces trivial homomorphism 364
Nulhomotopy lemma 377
One-point compactification 185
One-point compactification, uniqueness 183
One-to-one correspondence 18
Open covering 164
Open interval 25 84
Open map 92 137
Open ray 86
Open refinement 245
Open set 76
Open set, relative to subspace 89
Operation on schemes 460
Operation, binary 30
Orbit 490
Orbit space 199 490
Order of a covering 305
Order of a group 346
Order of a group element 412
Order relation 24
Order topology 84
Order topology vs. subspace topology 91
Order topology, compact subspaces 172
Order topology, Hausdorff condition 100
Order topology, normality 202 206
Order topology, subbasis 86
Order type 25
Ordered field 31
Ordered pair 13
Ordered square 90
Ordered square is linear continuum 155
Ordered square, connectedness 156
Ordered square, metrizability 194
Ordered square, path connectedness 156
Oriented edge of a graph 506
Oriented line segment 447
Paracompact space 253 (see also “Paracompactness”)
Paracompactness 253
Paracompactness and perfect maps 260
Paracompactness of 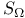 260 261 260 261
Paracompactness of 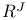 257 257
Paracompactness of  253 253
Paracompactness of 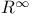 in box topology 260 in box topology 260
Paracompactness of  257 257
Paracompactness of closed subspace 254
Paracompactness of compact Hausdorff space 252
Paracompactness of metric space 257
Paracompactness of regular Lindelof space 257
Paracompactness of topological groups 261
Paracompactness vs. normality 253
Partial order 71
Partial order, axioms 87
Partial order, strict 68
Partition of a set 23
Partition of unity 225 258
Partition of unity, existence 225 259
Pasting edges together 448
Pasting lemma 108
Pasting regions together 458
Path 155
Path component 160
Path component vs. component 161
Path connectedness 155
Path connectedness of 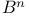 156 156
Path connectedness of  156 156
Path connectedness of 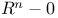 156 156
Path connectedness of long line 159
Path connectedness of ordered square 156
Path connectedness of topologist’s sine curve 157
Path connectedness vs. connectedness 156
Path homotopy 323
Path, corresponding to edge path 506
Path-homotopy class 324
Path-induced homomorphism 331
Peano curve 271
Peano space 275
Perfect map 172 199
Perfect map and compactness 172
Perfect map and paracompactness 260
Perfectly normal space 213
Piecewise linear function 302
Plane in 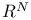 310 310
Point-finite collection 248
Point-finite family 227
Point-open topology 281
Point-open topology vs. compact convergence topology 285
Point-open topology vs. compact-open topology 285
Point-open topology, equals product topology 282
Pointwise bounded 278
Pointwise convergence topology 281 (see also “Point-open topology”)
Polygonal region 447
Positive integers 32
Positive linear map of intervals in R 328
Positive linear map of oriented line segments 447
Power set 12
Precise refinement 258
Preimage 19
Presentation of a group 425
Principle of Induction 32
Principle of induction, transfinite 67
Principle of recursive definition 47 54
Principle of recursive definition, general 72
Product of continuous maps 112
Product of covering maps 339
Product of open maps 141
Product of path-homotopy classes 326
Product of paths 326
Product of quotient maps 141 143 145 186 289
Product space 114 (see also “Product topology”)
Product topology 86 114
Product topology vs. box topology 115
Product topology vs. point-open topology 282
Product topology vs. quotient topology 141 143. 186 289
Product topology vs. subspace topology 89 116
Product topology vs. uniform topology 124
Product topology, basis 86 115 116
Product topology, closures in 101 116
Product topology, compactness 167 234
Product topology, complete regularity 211
Product topology, connectedness 150 152
Product topology, convergent sequences 118 265
Product topology, first-countability 191
Product topology, Hausdorff condition 100 116 196
| Product topology, Lindeloef condition 193
Product topology, local compactness 186
Product topology, metrizability 133 134
Product topology, normality 198 203
Product topology, paracompactness 257
Product topology, regularity 196
Product topology, second-countability 191
Product topology, subbasis 88 114
Products of covering map 339
Projection map 87 114
Projection map is open map 92
Projective n-space 373
Projective plane 372 (see also “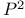 ”) ”)
Projective-type scheme 463
Proper inclusion 4
Proper labelling scheme 463
Proper subset 4
Properly discontinuous 490
Pruefer manifold 317
Punctured euclidean space 156 (see also “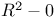 ”) ”)
Punctured plane 325 (see also “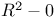 ”) ”)
Quantifiers, logical 9
Quasicomponent 163
Quasicomponent vs. component 163 236
Quotient group 331
Quotient map 137
Quotient map, composites 141
Quotient map, products 141 143 145 186 289
Quotient map, restrictions 137 138 140
Quotient space 139 (see also “Quotient topology”)
Quotient topology 138
Quotient topology and continuous functions 142
Quotient topology, 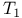 condition 141 condition 141
Quotient topology, Hausdorff condition 142 199
Quotient topology, local compactness 199
Quotient topology, local connectedness 163
Quotient topology, normality 199
Quotient topology, regularity 199
Quotient topology, second-countability 199
Quotient topology, vs. product topology 141 143 145 186 289
Range of a function 16
Rank of a free abelian group 411
Rational number 32
Ray in ordered set 85
Recursive definition, principle 47 54
Recursive definition, principle, general principle 72
Reduced edge path 507
Reduced word 413
refinement 245 305
Regular covering space 489
Regular covering space is orbit space 491
Regular Lindeloef space metrizability 218
Regular Lindeloef space normality 205
Regular Lindeloef space paracompactness 257
Regular space 195 (see also “Regularity”)
Regularity 195
Regularity and perfect maps 199
Regularity of G/H 146
Regularity of locally compact Hausdorff space 205
Regularity of manifold 227
Regularity of orbit space 199
Regularity of products 196
Regularity of subspaces 196
Regularity of topological groups 146
Regularity vs. complete regularity 214
Regularity vs. Hausdorff condition 195 197
Regularity vs. metrizability 215
Regularity vs. normality 195 198 203
Relation 21
Relation on a free group 424
Relation on a free group complete set 425
Represented by a word 412
Restriction of a covering map 338 484
Restriction of a function 17
Restriction of a quotient map 137 138 140
Restriction of a relation 28
retract 223 348
Retraction 335 348
Retraction as quotient map 144
Reverse of a path 327
Right coset 330
Right inverse 21
Rule of assignment 15
Russell’s paradox 62
Saturated set 137
Scheme 449
Scheme, projective type 463
Scheme, proper 463
Scheme, torus type 463
Schoenflies theorem 392
Schroeder — Bemstein theorem 52
Second category set 295
Second coordinate of ordered pair 13
Second-countability 190
Second-countability and perfect maps 199
Second-countability of  and and  and and  190 190
Second-countability of  in uniform topology 190 in uniform topology 190
Second-countability of 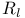 192 192
Second-countability of 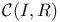 194 194
Second-countability of compact metric space 194
Second-countability of orbit space 199
Second-countability of products 191
Second-countability of subspace 191
Second-countability of topological group 195
Second-countability vs. countable dense subset 194
Second-countability vs. Lindeleof condition 194
Second-countable space 190 (see also “Second-countability”)
Section of a well-ordered set 66
Section of the positive integers 32
Seifert-van Kampen theorem 426
Seifert-van Kampen theorem, classical version 431
Seifert-van Kampen theorem, special case 369
Semilocally simply connected 494
Separable 192 (see also “Countable dense subset”)
Separates a space 378
Separates a space, into n components 378
Separates points from closed sets 218
Separation 148
Separation by continuous functions 211
Separation theorem, closed topologist’s sine curve in  393 393
Separation theorem, general 380 392
Separation theorem, simple closed curve in  379 390 379 390
Separation theorem, theta space in  395 395
Sequence lemma 130
Sequences 38
Sequences and closure 130 190
Sequences and continuity 130 190
Sequential compactness 179
Sequential compactness vs. compactness 179
Shrinking lemma 227
Shrinking lemma, general 258
Shrinking map 182
Shrinking map and fixed points 182
Shrinking map vs. contraction 182
Simple closed curve 379
Simple closed curve, generates 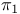 of of  401 401
Simple closed curve, separates  379 390 379 390
Simple closed curve, winding number 404 406
Simple loop 404
Simple order 24
Simply connected 333
Simply connected vs. locally simply connected 499
Simply connected,  369 369
Simply connected, star-convex set 334
Simply connected, tree 508
Slice in covering space 336
Slice in product space 167
Smaller topology 77
Smallest element of ordered set 27
Smirnov metrization theorem 261
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



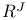
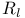
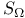

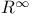 in box topology
in box topology 
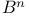

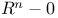
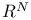
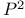 ”)
”)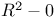 ”)
”)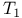 condition
condition  and
and 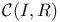

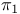 of
of 