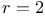|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Matousek J. — Lectures on Discrete Geometry (some chapters) |
|
|
 |
| Предметный указатель |
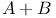 (Minkowski sum) 280 (Minkowski sum) 280
 (-kth. function in Ackermann hierarchy) 167 (-kth. function in Ackermann hierarchy) 167
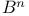 (unit ball in (unit ball in 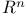 ) 11 ) 11
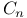 (Hamming cube) 314 (Hamming cube) 314
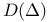 (denning set) 152 (denning set) 152
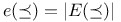 286 286
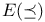 (linear extensions) 286 (linear extensions) 286
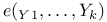 (number of edges on the (number of edges on the 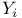 ) 214 ) 214
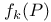 (number of k-faces) 96 (number of k-faces) 96
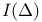 (intersecting objects) 149 (intersecting objects) 149
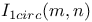 (number of point-unit circle incidences) 50 (number of point-unit circle incidences) 50
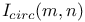 (number of point-circle incidences) 53 (number of point-circle incidences) 53
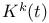 (complete k-partite hypergraph) 204 (complete k-partite hypergraph) 204
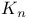 12 12
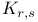 (complete bipartite graph) 69 (complete bipartite graph) 69
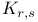 -free graph 69 72 -free graph 69 72
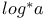 (iterated logarithm) 11 (iterated logarithm) 11
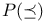 (order polytope) 286 (order polytope) 286
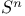 (unit sphere in $\mathbf R^{n+1}) 295 (unit sphere in $\mathbf R^{n+1}) 295
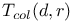 (colored Tverberg number) 194 (colored Tverberg number) 194
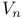 (volume of unit n-ball) 293 (volume of unit n-ball) 293
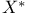 (dual set) 82 (5.1.3) (dual set) 82 (5.1.3)
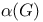 (independence number) 274 (independence number) 274
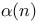 (inverse Ackermann) 167 (inverse Ackermann) 167
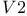 11 11
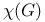 (chromatic number) 274 (chromatic number) 274
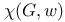 (weighted chromatic number) 275 (weighted chromatic number) 275
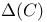 (lattice constant) 35 (lattice constant) 35
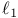 -ball see Crosspolytope -ball see Crosspolytope
 (countable sequences with (countable sequences with  -norm) 333 -norm) 333
 -novm. 333 -novm. 333
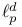 ( (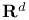 with with  norm) 333 norm) 333
 -dense set 295 -dense set 295
 -net 295 -net 295
 -net, application 304 318 320 339 342 -net, application 304 318 320 339 342
 -separated set 295 -separated set 295
 conjecture 290 conjecture 290
 (Gamma function) 293 (Gamma function) 293
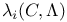 (i-th successive minimum) 35 (i-th successive minimum) 35
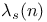 (maximum length of DS sequence) 161 (maximum length of DS sequence) 161
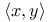 (scalar product) 11 (scalar product) 11
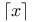 (ceiling function) 11 (ceiling function) 11
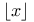 (floor function) 11 (floor function) 11
![$\mathbf E[X]$](/math_tex/590e5e8eb8aae60cd7eee628b3ef6abd82.gif) (expectation) 11 (expectation) 11
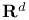 13 13
 (duality) 83 (duality) 83
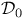 (duality) 80 (5.1.1) (duality) 80 (5.1.1)
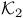 (planar convex sets) 227 (planar convex sets) 227
 (squared Euclidean metrics) 349 (squared Euclidean metrics) 349
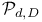 (sets definable by polynomials) 232 (10.3.2) (sets definable by polynomials) 232 (10.3.2)
 ((p,q)-theorem) 243 (10.5.1) ((p,q)-theorem) 243 (10.5.1)
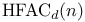 (number of halving facets) 253 (number of halving facets) 253
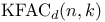 (maximum number of k-facets) 252 (maximum number of k-facets) 252
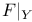 (restriction of set system) 227 (restriction of set system) 227
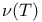 (packing number) 222 (packing number) 222
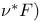 (fractional packing number) 222 (fractional packing number) 222
 (simple k-packing number) 225 (Ex.4) (simple k-packing number) 225 (Ex.4)
 (asymptotically at least) 11 (asymptotically at least) 11
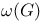 (clique number) 274 (clique number) 274
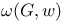 (weighted clique number) 275 (weighted clique number) 275
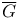 (graph complement) 274 (graph complement) 274
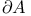 (boundary) 11 (boundary) 11
 125 (6.1) 125 (6.1)
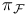 (shatter function) 228 (shatter function) 228
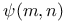 (length of m-decomposable DS-sequence) 171 (length of m-decomposable DS-sequence) 171
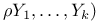 (hypergraph density) 214 (hypergraph density) 214
 (lower envelope of segments, complexity) 160 (lower envelope of segments, complexity) 160
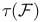 (transversal number) 221 (transversal number) 221
 (fractional transversal number) 222 (fractional transversal number) 222
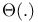 (same order) 11 (same order) 11
 -approximation 231 -approximation 231
 -net 226 (10.2.1) 227 -net 226 (10.2.1) 227
 -net, size 228 (10.2.4) -net, size 228 (10.2.4)
 -net, weak 248 (10.6.3) -net, weak 248 (10.6.3)
 -net, weak, for convex sets 240 (10.4.1) -net, weak, for convex sets 240 (10.4.1)
 -pushing 101 -pushing 101
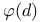 (Euler's function) 58 (Euler's function) 58
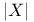 11 11
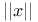 (Euclidean norm) 11 (Euclidean norm) 11
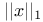 ( (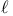 -norm) 85 -norm) 85
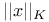 (norm induced by K) 321 (norm induced by K) 321
 ( ( -norm) 332 -norm) 332
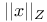 (general norm) 321 (general norm) 321
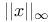 (maximum norm) 85 333 (maximum norm) 85 333
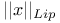 (Lipschitz norm) 332 (Lipschitz norm) 332
(p,q)-condition 243
(p,q)-theorem 243 (10.5.1)
(p,q)-theorem, for hyperplane transversals 246 (10.6.1)
0 (.) (asymptotically at most) 11
A(n) (Ackermann function) 167
Ackermann function 167
AffDep(a) 108
Affine combination 13
Affine dependence 14
Affine Gale diagram 110
Affine hull 13
Affine mapping 15
Affine subspace 13
Affinely isomorphic arrangements 131
AffVal(a) 108
Alexandrov — Fenchel inequality 284
Algebraic geometry 129
Algebraic number 32 (Ex.4)
Algebraic surface patches, lower envelope 181
Algebraic surface patches, single cell 183 (7.7.2)
Algebraic surfaces, arrangement 128
Algebraic surfaces, decomposition problem 156
Algorithm, convex hull 87 104
Algorithm, for 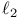 -embedding 351 -embedding 351
Algorithm, for volume approximation 297 302
Algorithm, Goemans — Williamson for MAXCUT 353 (Ex.5)
Algorithm, greedy 225 225
Algorithm, LLL 36
Algorithm, simplex, randomized 94
Almost convex set 47 48
Almost spherical projection 329
Almost spherical section of convex body 322 (14.4.5) 325
Almost spherical section of crosspolytope 323 329
Almost spherical section of cube 320
Almost spherical section of ellipsoid 319 (14.4.1)
Antichain 278 (Ex.4)
Approximation by fraction 31 (2.1.3) 32 32
Approximation of volume 302
Approximation of volume, hardness 297
ARC 60
Arithmetic progression, generalized 54
Arithmetic progression, primes in 58 (4.2.4)
Arithmetic progression, Szemeredi's theorem 217
Arrangement of arbitrary sets 128
Arrangement of hyperplanes 124
Arrangement of hyperplanes, number of cells 125 (6.1.1)
Arrangement of hyperplanes, unbounded cells 126 (Ex.2)
Arrangement of lines 50
Arrangement of pseudolines 129 133 255
Arrangement of pseudosegments 255
Arrangement of segments 127
Arrangement, affine isomorphism 131
Arrangement, central 126
Arrangement, isomorphism 131
Arrangement, many cells 51 53 63 147
Arrangement, realization space 134
Arrangement, simple 125
Arrangement, stretchable 131 134
Arrangement, triangulation 75 (Ex.2) 154
Art gallery 234 238
Atomic lattice 90
B(x, r) (r-ball centered at x) 11
Balanced line 265
Balinski's theorem 89
Ball, 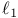 see Crosspolytope see Crosspolytope
| Ball, random point in 294
Ball, smallest enclosing 24 (Ex.5)
Ball, volume 293
Banach spaces, local theory 309 315
Banach — Mazur distance 323
Bandwidth 363
Basis (lattice) 32
Basis, reduced 36
Bezdek's conjecture 52
bi-Lipschitz mapping 332
Binomial distribution 229
Bipartite graph 12
Bisection width 62
bisector 118
Blaschke — Santalo inequality 301
Body, convex, almost spherical 319
Body, convex, almost spherical section 322 (14.4.5) 325
Body, convex, approximation by ellipsoids 305 (13.4.1)
Body, convex, lattice points in 29—38
Body, convex, volume approximation 297 302
Borsuk — Ulam theorem, application 26 196
Bottom-vertex triangulation 154 156
Brick set 282
Brunn — Minkowski inequality 280 (12.2.2)
Brunn — Minkowski inequality, application 311 313
Brunn — Minkowski inequality, dimension-free form 284 (Ex.5)
Brunn's inequality 280 (12.2.1)
Brunn's inequality, application 289
Busemann — Petty problem 295
Cage representation 93
Canonical triangulation see Bottom-vertex triangulation
CAP 40
Cap, spherical (volume) 313
Caratheodory's theorem 17 (1.2.3) 19
Caratheodory's theorem, application 191 200 300
Caratheodory's theorem, colorful 190 (8.2.1)
Caratheodory's theorem, colorful, applicaton 193
Cauchy — Schwarz inequality 12
Cell of arrangement 51 124 127
Cell, complexity, in higher dimensions 183 184
Cell, complexity, in the plane 169
Center transversal theorem 27 (1.4.4)
Centerpoint 25 (1.4.1) 202
Centerpoint theorem 26 (1.4.2) 195
Central arrangement 126
Chain 278 (Ex.4)
Chain polytope 291
Chebyshev's inequality 229
Chirotope 208
Chromatic number 274
Circles, cutting lemma 75
Circles, incidences 53 67 67 73 73 76
Circles, touching (and planar graphs) 93
Circles, unit, incidences 50 55 57 63 73
Circles, unit, Sylvester-like result 52
Circumradius 299 (13.2.2)
Circumradius, approximation 302
Clarkson's theorem on levels 137 (6.3.1)
Clique number 274
Closed from above (or from below) 46
Closest pair, computation 119
Coatomic lattice 91
Colored Helly theorem 189 (Ex.2)
Colored Tverberg theorem 194 (8.3.3)
Colored Tverberg theorem, application 204
Colored Tverberg theorem, for 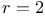 196 196
Colorful Caratheodory theorem 190 (8.2.1)
Colorful Caratheodory theorem, applicaton 193
Combination, affine 13
Combination, convex 17
Combinatorially equivalent polytopes 90 (5.3.4)
Combinatorics, polyhedral 273
Compact set 12
Comparability graph 278 (Ex.4) 291
Complete graph 12
Complex plane, point-line incidences 52
Complex, simplicial, d-collapsible 189
Complex, simplicial, d-Leray 189
Complex, simplicial, d-representable 189
Complex, simplicial, Van Kampen-Flores 342
Complexity, of cell 159
Compression, path 169
Concentration for Hamming cube 315 (14.2.3)
Concentration for sphere 310 (14.1.1)
Concentration Gaussian 314 (14.2.2)
Concentration of projection 334 (15.2.2)
Conductance (of graph) 346
Cone of squared Euclidean metrics 349
cone(X) 192
Cone, convex 20 (Ex.5) 192
Cone, metric 105 349
Conjecture,  290 290
Conjecture, Bezdek's 52
Conjecture, d-step 94
Conjecture, Dirac — Motzkin 56
Conjecture, Fueredi — Hajnal 170
Conjecture, Gruenbaum — Motzkin 248
Conjecture, Hirsch 94
Conjecture, Kalai's 195
Conjecture, perfect graph, strong 275
Conjecture, perfect graph, weak 275
Conjecture, Purdy's 54
Conjecture, Reay's 19
Conjecture, Ryser's 225
Conjecture, Sierksma's 196
Conjecture, Stanley — Wilf 170
Connected graph 12
Constant, lattice 35
Continuous motion argument 268
Continuous upper bound theorem 112
conv(.X") (convex hull) 17
Convex body, almost spherical 319
Convex body, almost spherical section 322 (14.4.5) 325
Convex body, approximation by ellipsoids 305 (13.4.1)
Convex body, lattice points in 29—38
Convex body, volume approximation 297 302
Convex combination 17
Convex cone 20 (Ex.5) 192
Convex function 12
Convex hull 17
Convex hull of random points 99 305
Convex hull, algorithm 87 104
Convex independent set 40 (3.1.1)
Convex independent set in grid 43 (Ex.2)
Convex polygons, union complexity 185
Convex polyhedron 85
Convex polytope 85
Convex polytope, almost spherical, number of facets 320 (14.4.2)
Convex polytope, integral, cvirefex:hoffm-int 278
Convex polytope, number of 135 (Ex.3)
Convex polytope, realization 134
Convex polytope, symmetric, number of facets 324 (14.4.2)
Convex polytope, volume, lower bound 303
Convex polytope, volume, upper bound 297 (13.2.1)
Convex polytopes, union complexity 185
Convex position 40
Convex set 17 (1.2.1)
Convex sets, in general position 42
Convex sets, intersection patterns 189
Convex sets, transversal 243 (10.5.1)
Convex sets, upper bound theorem 189
Convex sets, VC-dimension 227
Copies, similar (counting) 53 56
cr(G) (crossing number) 60
cr(X) (crossing number of halving-edge graph) 268
Criterion, Gale's 97 (5.4.4)
Cross-ratio 54
Crossing (in graph drawing) 60
Crossing edges, pairwise 169
Crossing number 60
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



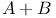 (Minkowski sum)
(Minkowski sum)  (-kth. function in Ackermann hierarchy)
(-kth. function in Ackermann hierarchy) 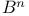 (unit ball in
(unit ball in 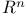 )
) 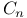 (Hamming cube)
(Hamming cube) 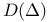 (denning set)
(denning set) 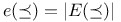
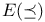 (linear extensions)
(linear extensions) 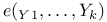 (number of edges on the
(number of edges on the 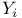 )
) 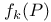 (number of k-faces)
(number of k-faces) 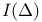 (intersecting objects)
(intersecting objects) 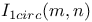 (number of point-unit circle incidences)
(number of point-unit circle incidences) 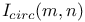 (number of point-circle incidences)
(number of point-circle incidences) 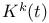 (complete k-partite hypergraph)
(complete k-partite hypergraph) 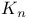
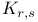 (complete bipartite graph)
(complete bipartite graph) 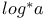 (iterated logarithm)
(iterated logarithm) 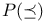 (order polytope)
(order polytope) 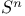 (unit sphere in $\mathbf R^{n+1})
(unit sphere in $\mathbf R^{n+1}) 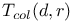 (colored Tverberg number)
(colored Tverberg number) 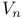 (volume of unit n-ball)
(volume of unit n-ball) 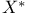 (dual set)
(dual set) 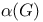 (independence number)
(independence number) 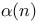 (inverse Ackermann)
(inverse Ackermann) 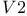
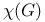 (chromatic number)
(chromatic number) 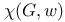 (weighted chromatic number)
(weighted chromatic number) 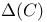 (lattice constant)
(lattice constant) 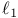 -ball
-ball  (countable sequences with
(countable sequences with 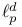 (
(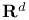 with
with  -dense set
-dense set  conjecture
conjecture  (Gamma function)
(Gamma function) 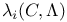 (i-th successive minimum)
(i-th successive minimum) 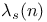 (maximum length of DS sequence)
(maximum length of DS sequence) 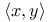 (scalar product)
(scalar product) 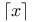 (ceiling function)
(ceiling function) 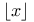 (floor function)
(floor function) ![$\mathbf E[X]$](/math_tex/590e5e8eb8aae60cd7eee628b3ef6abd82.gif) (expectation)
(expectation)  (duality)
(duality)  (duality)
(duality) 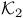 (planar convex sets)
(planar convex sets)  (squared Euclidean metrics)
(squared Euclidean metrics) 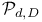 (sets definable by polynomials)
(sets definable by polynomials)  ((p,q)-theorem)
((p,q)-theorem) 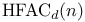 (number of halving facets)
(number of halving facets) 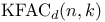 (maximum number of k-facets)
(maximum number of k-facets) 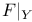 (restriction of set system)
(restriction of set system) 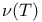 (packing number)
(packing number) 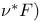 (fractional packing number)
(fractional packing number)  (simple k-packing number)
(simple k-packing number)  (asymptotically at least)
(asymptotically at least) 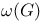 (clique number)
(clique number) 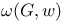 (weighted clique number)
(weighted clique number) 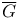 (graph complement)
(graph complement) 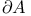 (boundary)
(boundary) 
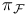 (shatter function)
(shatter function) 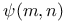 (length of m-decomposable DS-sequence)
(length of m-decomposable DS-sequence) 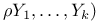 (hypergraph density)
(hypergraph density)  (lower envelope of segments, complexity)
(lower envelope of segments, complexity) 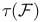 (transversal number)
(transversal number)  (fractional transversal number)
(fractional transversal number) 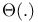 (same order)
(same order)  -approximation
-approximation 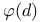 (Euler's function)
(Euler's function) 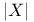
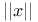 (Euclidean norm)
(Euclidean norm) 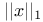 (
(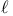 -norm)
-norm) 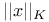 (norm induced by K)
(norm induced by K)  (
(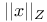 (general norm)
(general norm) 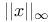 (maximum norm)
(maximum norm) 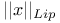 (Lipschitz norm)
(Lipschitz norm) 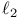 -embedding
-embedding