|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Matousek J. — Lectures on Discrete Geometry (some chapters) |
|
|
 |
| Предметный указатель |
Simplicial complex, d-collapsible 189
Simplicial complex, d-Leray 189
Simplicial complex, d-representable 189
Simplicial polytope 91 (5.3.6)
Simplicial sphere 103
Simplification (of level) 76
Single cell in higher dimensions 183 184
Single cell in the plane 169
Site (in Voronoi diagram) 113
Smallest enclosing ball 24 (Ex.5)
Smallest enclosing ellipsoid, computation 307
SO(N) 318
SO(n), measure concentration 314
Sobolev inequalities, logarithmic 315
Sorting with partial information 285—291
Space,  333 333
Space, Hilbert 333
Space, metric 331
Space, realization 134
Spanner 343 (Ex.2)
Spanning tree, minimum 120 (Ex.5)
Sphere, measure concentration 310 (14.1.1)
Sphere, simplicial 103
Spherical cap 313
Spherical polytope 121 (Ex.10)
STAB(G) (stable set polytope) 277
Stable set see Independent set
Stable set polytope 277
Stanley — Wilf conjecture 170
Starshaped 24 (Ex.7)
Steinitz theorem 20 89 93
Steinitz theorem, quantitative 94
Stretchability 131 134
Strong perfect graph conjecture 275
Strong upper bound theorem 104
Subgraph 12
Subgraph, forbidden 69
Subgraph, induced 274
Subgraphs, transversal 249
Subgroup, discrete, of Rd 33
Subhypergraph 203
Subsequence, monotone 278 (Ex.4)
Subset sum problem 36
Subspace, affine 13
Subspace, linear 13
Subspace, random 317
Successive minimum 35
Sum of squares of cell complexities 146 (Ex.1)
Sum, Minkowski 280
Sums and products 56 (Ex.8)
Superimposed projections of lower envelopes 184
Surface patches, algebraic, lower envelope 181
Surface patches, algebraic, single cell 183 (7.7.2)
Surfaces, algebraic, arrangement 128
Surfaces, decomposition problem 156
Sylvester's problem 51
Szemeredi regularity lemma 214 217
Szemeredi — Trotter theorem 49 (4.1.1)
Szemeredi — Trotter theorem, application 56 (Ex.5) 56 56 56 65 67
Szemeredi — Trotter theorem, in the complex plane 52
Szemeredi — Trotter theorem, proof 61 70 72
T(d, r) (Tverberg number) 191
t-almost spherical body 319
Tessellation, Dirichlet see Voronoi diagram
Theorem, (p,q) 243 (10.5.1)
Theorem, (p,q), for hyperplane transversals 246 (10.6.1)
Theorem, Balinski's 89
Theorem, Borsuk — Ulam, application 26 196
Theorem, Caratheodory's 17 (1.2.3) 19
Theorem, Caratheodory's, application 191 200 300
Theorem, center transversal 27 (1.4.4)
Theorem, centerpoint 26 (1.4.2) 195
Theorem, Clarkson's, on levels 137 (6.3.1)
Theorem, colored Helly 189 (Ex.2)
Theorem, colored Tverberg 194 (8.3.3)
Theorem, colored Tverberg, application 204
Theorem, colored Tverberg, for 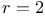 196 196
Theorem, colorful Caratheodory 190 (8.2.1)
Theorem, colorful Caratheodory, applicaton 193
Theorem, crossing number 60 (4.3.1)
Theorem, crossing number, application 61 66 73 268
Theorem, crossing number, for multigraphs 65 (4.4.2)
Theorem, Dilworth's 278 (Ex.4)
Theorem, Dirichlet's 58
Theorem, Dvoretzky's 325 (14.6.1) 329
Theorem, Edmonds', matching polytope 277
Theorem, efficient comparison 286 (12.3.1)
Theorem, Elekes — Ronyai 54
Theorem, epsilon-net 228 (10.2.4)
Theorem, epsilon-net, application 235 239
Theorem, epsilon-net, if and only if form 240
Theorem, Erdos — Simonovits 204 (9.2.2)
Theorem, Erdos — Szekeres 40 (3.1.3)
Theorem, Erdos — Szekeres, application 44
Theorem, Erdos — Szekeres, generalizations 42
Theorem, Erdos — Szekeres, positive-fraction 211 (9.3.3) 213
Theorem, Erdos — Szekeres, quantitative bounds 42
Theorem, fractional Helly 187 (8.1.1)
Theorem, fractional Helly, application 200 203 245
Theorem, fractional Helly, for line transversals 247 (10.6.2)
Theorem, g-theorem 104
Theorem, Hadwiger's transversal 248
Theorem, Hahn — Banach 19
Theorem, Hall's, marriage 225
Theorem, ham-sandwich 26 (1.4.3)
Theorem, ham-sandwich, application 209
Theorem, Helly's 21 (1.3.2)
Theorem, Helly's, application 23 (Ex.2) 24 25 83 188 191
Theorem, Helly-type 248 250
Theorem, Helly-type, for containing a ray 24 (Ex.6)
Theorem, Helly-type, for lattice points 279 (Ex.7)
Theorem, Helly-type, for line transversals 84 (Ex.9)
Theorem, Helly-type, for separation 25 (Ex.9)
Theorem, Helly-type, for visibility 25 (Ex.7)
Theorem, Helly-type, for width 23 (Ex.4)
Theorem, Kirchberger's 25 (Ex.9)
Theorem, Koebe's 93
Theorem, Koevari — Sos — Turan 69 (4.5.2)
Theorem, Konig's, edge-covering 225 278
Theorem, Krasnosel'skii's 25 (Ex.7)
Theorem, Kruskal — Hoffman 278 (Ex.6)
Theorem, Lagrange's, four-square 38 (Ex.2.3.1)
Theorem, lattice basis 34 (2.2.2)
Theorem, Lawrence's, representation 133
Theorem, Lipton — Tarjan 62
Theorem, lower bound, generalized 104
Theorem, lower bound, generalized, application 264
Theorem, Milnor — Thom 128 132
Theorem, Minkowski — Hlawka 35
Theorem, Minkowski's 29 (2.1.1)
Theorem, Minkowski's, for general lattices 33 (2.2.1)
Theorem, Minkowski's, second 35
Theorem, Pappus 131
Theorem, Preiman's 54
Theorem, prime number 58
Theorem, Ramsey's 39
Theorem, Ramsey's, application 40 42 43 48 99 346
Theorem, Sard's 16
Theorem, separation 18 (1.2.4)
Theorem, separation, application 19 82 304 350
Theorem, separator 62
Theorem, seven-hole 45 (3.2.2)
Theorem, Steinitz 89 (5.3.3) 93
Theorem, Steinitz's 20
Theorem, Steinitz, quantitative 94
Theorem, Szemeredi — Trotter 49 (4.1.1)
Theorem, Szemeredi — Trotter, application 56 (Ex.5) 56 56 56 65 67
Theorem, Szemeredi — Trotter, in the complex plane 52
Theorem, Szemeredi — Trotter, proof 61 70 72
Theorem, Tverberg's 192 (8.3.1)
| Theorem, Tverberg's, application 200
Theorem, Tverberg's, positive-fraction 211
Theorem, Tverberg's, proofs 195
Theorem, two-square 37 (2.3.1)
Theorem, upper bound 100 (5.5.1) 103
Theorem, upper bound, and k-facets 264
Theorem, upper bound, application 117
Theorem, upper bound, continuous analogue 112
Theorem, upper bound, for convex sets 189
Theorem, upper bound, formulation with h-vector 103
Theorem, upper bound, proof 266 (Ex.6)
Theorem, upper bound, strong 104
Theorem, weak epsilon-net 241 (10.4.2)
Theorem, weak epsilon-net, another proof 242 (Ex.1)
Theorem, weak epsilon-net, application 245
Theorem, zone 142 (6.4.1)
Theorem, zone, planar 162 (Ex.5)
Thiessen polygons 117
Topological plane 133
Torus, n-dimensional, measure concentration 314
Total unimodularity 277 278
Trace (of set system) 227
Transform, duality 80 (5.1.1) 83
Transform, Gale 106
Transform, Gale, application 202 266
Transform, medial axis 117
Transversal 84 (Ex.9) 221
Transversal number 221
Transversal number, bound using 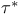 225 231 225 231
Transversal of convex sets 243 (10.5.1)
Transversal of d-intervals 248 249
Transversal of discs 221 249
Transversal of subgraphs 249
Transversal same-type 208
Transversal theorem, Hadwiger's 248
Transversal, criterion of existence 209 (9.3.2)
Transversal, fractional 222
Transversal, fractional, bound 244 (10.5.2)
Transversal, fractional, for infinite systems 224
Transversal, hyperplane 246 (10.6.1) 248
Transversal, line 248
Traveling salesman polytope 273
Tree metric 360 364 365 365 365
Tree volume 363
Tree, hierarchically well-separated 364
Tree, spanning, minimum 120 (Ex.5)
Treewidth 249
Triangle, generalized 70 (4.5.3)
Triangles, fat, union complexity 185
Triangles, level in arrangement 176
Triangles, lower envelope 175 (7.5.1) 178
Triangles, VC-dimension 238 (Ex.1)
Triangulation, bottom-vertex 154 156
Triangulation, canonical see Bottom-vertex triangulation
Triangulation, Delaunay 115 118 120
Triangulation, of arrangement 75 (Ex.2)
Tverberg partition 192
Tverberg point 192
Tverberg's theorem 192 (8.3.1)
Tverberg's theorem, application 200
Tverberg's theorem, colored 194 (8.3.3)
Tverberg's theorem, colored, application 204
Tverberg's theorem, colored, for 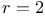 196 196
Tverberg's theorem, positive-fraction 211
Tverberg's theorem, proofs 195
Two-square theorem 37 (2.3.1)
Type, order 207 212
U(n) (number of unit distances) 50
Unbounded cells, number of 126 (Ex.2)
Uniform measure 227
Unimodularity, total 277 278
Union, complexity 185
Union, complexity, for discs 120 (Ex.9)
UNION-FIND problem 169
Unit circles, incidences 50 55 57 63 73
Unit circles, Sylvester-like result 52
Unit distances 50
Unit distances and incidences 55 (Ex.1)
Unit distances for convex position 52
Unit distances in 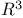 52 52
Unit distances in 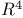 52 55 52 55
Unit distances in the plane 52
Unit distances lower bound 57 (4.2.2)
Unit distances on 2-sphere 52
Unit distances upper bound 63 (Ex.2)
Unit paraboloid 116
Universality of cyclic polytope 99 (Ex.3)
Up-set 286
Upper Bound Theorem 100 (5.5.1) 103
Upper bound theorem, and k-facets 264
Upper bound theorem, application 117
Upper bound theorem, continuous analogue 112
Upper bound theorem, for convex sets 189
Upper bound theorem, formulation with /i-vector 103
Upper bound theorem, proof 266 (Ex.6)
Upper bound theorem, strong 104
V(G) (vertex set) 11
V(x) (visibility region) 235
V-polytope 84 (5.2.1)
Van Kampen-Flores simplicial complex 342
Vapnik — Chervonenkis dimension see VC-dimension
VC-dimension 227 (10.2.3)
VC-dimension, bounds 232 (10.3.2) 233
VC-dimension, f-vector 96
VC-dimension, f-vector, of representable complex 189
VC-dimension, for halfspaces 232 (10.3.1)
VC-dimension, for triangles 238 (Ex.1)
VC-dimension, g-vector 104
VC-dimension, h-vector 102
VC-dimension, shortest (lattice) 36
VC-dimension, sign (of a face) 124
Veronese mapping 232
Vertex of arrangement 51 127
Vertex of polytope 88
Vertical decomposition 75 (Ex.3) 150
Visibility 234
Visibility, Helly-type theorem 25 (Ex.7)
vol(A) 11
Volume of ball 293
Volume of polytope, lower bound 303
Volume of polytope, upper bound 297 (13.2.1)
Volume of regular simplex 300
Volume, approximation 302
Volume, approximation, hardness 297
Volume, mixed 284
Volume, tree 363
Volume-respecting embedding 362
Voronoi diagram 113
Voronoi diagram, abstract 118
Voronoi diagram, complexity 117 (5.7.4) 119 184
Voronoi diagram, farthest-point 117
Voronoi diagram, higher-order 119
Weak  -net 248 (10.6.3) -net 248 (10.6.3)
Weak  -net, for convex sets 240 (10.4.1) -net, for convex sets 240 (10.4.1)
Weak epsilon-net theorem 241 (10.4.2)
Weak epsilon-net theorem, another proof 242 (Ex.1)
Weak epsilon-net theorem, application 245
Weak perfect graph conjecture 275
Weak regularity lemma 214 (9.4.1)
Weak regularity lemma, application 217 (Ex.2) 219
width 23 (Ex.4)
Width, approximation 302 303
Width, bisection 62
Wigner — Seitz zones 117
Wiring diagram 130
x-monotone (curve) 76
X-simplex 199
Zarankiewicz problem 72
Zone in segment arrangement 145
Zone of algebraic variety 145 146
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




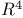
 -net
-net