|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Matousek J. — Lectures on Discrete Geometry (some chapters) |
|
|
 |
| Предметный указатель |
Crossing number and forbidden subgraph 62
Crossing number theorem 60 (4.3.1)
Crossing number theorem, application 61 66 73 268
Crossing number theorem, for multigraphs 65 (4.4.2)
Crossing number, odd 62
Crossing number, pairwise 62
Crosspolytope 85
Crosspolytope, almost spherical section 323 329
Crosspolytope, faces 89
Crosspolytope, projection 87 (Ex.2)
Cryptography 36
cube 85
Cube, almost spherical section 320
Cube, faces 90
Cube, Hamming 314
Cube, Hamming, embedding into 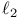 343 343
Cube, Hamming, measure concentration 315 (14.2.3)
Cubes, union complexity 185
Cup 40
Curve, moment 97 (5.4.1)
Curves, cutting into pseudosegments 73 256 257 257
Curves, incidences 53
Curves, lower envelope 160 179
Curves, single cell 169
Cutting 70
Cutting lemma 70 (4.5.3) 72
Cutting lemma, application 248
Cutting lemma, for circles 75
Cutting lemma, higher-dimensional 154 (6.5.3)
Cutting lemma, lower bound 74
Cutting lemma, proof 74 77 148 156 238
Cutting, on the average 72
Cyclic polytope 97 (5.4.3)
Cyclic polytope, universality 99 (Ex.3)
Cylinders, union complexity 185
d-collapsible simplicial complex 189
D-embedding 332 (15.1.1)
d-intervals, transversal 248 249
d-Leray simplicial complex 189
d-representable simplicial complex 189
d-step conjecture 94
Davenport — Schinzel sequence 160
Davenport — Schinzel sequence, asymptotics 167
Davenport — Schinzel sequence, decomposable 171
Davenport — Schinzel sequence, generalized 168 169
Davenport — Schinzel sequence, realization by curves 162 (Ex.1)
Decomposition problem 156
Decomposition, vertical 75 (Ex.3) 150
Deep below 45
Defining set 152
deg(z) (degree in halving-edge graph) 268
Degree 12
Dehn — Sommerville relations 103
Delaunay triangulation 115 118 120
Delone see Delaunay
Dense set 43
Density of graph, local 363
Density of hypergraph 214
Dependence, affine 14
det  33 33
Determinant and affine dependence 14
Determinant and orientation 208
Determinant and volume 37 (Ex.1)
Determinant of lattice 33
Diagram, Gale 110
Diagram, power 118
Diagram, Voronoi 113
Diagram, Voronoi, abstract 118
Diagram, Voronoi, complexity 117 (5.7.4) 119 184
Diagram, Voronoi, farthest-point 117
Diagram, Voronoi, higher-order 119
Diagram, wiring 130
Diameter and smallest enclosing ball 24 (Ex.5)
Diameter approximation 302
Dilworth's Theorem 278 (Ex.4)
dim(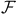 ) (VC-dimension) 227 (10.2.3) ) (VC-dimension) 227 (10.2.3)
Dimension of polytope 85
Dimension Vapnik-Chervonenkis see VC-dimension
Dimension, VC-dimension 227 (10.2.3)
Dirac — Motzkin conjecture 56
Dirichlet tessellation see Voronoi diagram
Dirichlet's theorem 58
Disc, largest empty, computation 119
Discrete subgroup of Rd 33
Discs, transversal 221 249
Discs, union complexity 120 (Ex.9) 185
Distance, Banach — Mazur 323
Distances, distinct 50 64
Distances, distinct, bounds 52
Distances, unit 50
Distances, unit, and incidences 55 (Ex.1)
Distances, unit, for convex position 52
Distances, unit, in 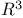 52 52
Distances, unit, in 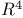 52 55 52 55
Distances, unit, in the plane 52
Distances, unit, lower bound 57 (4.2.2)
Distances, unit, on 2-sphere 52
Distances, unit, upper bound 63 (Ex.2)
Distortion 332 (15.1.1)
Distribution, binomial 229
Distribution, normal 314 328
Divisible point 195
Domains of action 117
Dominated (pseudo) metric 358
Double-description method 87
Drawing (of graph) 60
Drawing (of graph), on grid 94
Drawing (of graph), rubber-band 93
Dual polytope 91
Dual set 82 (5.1.3)
Dual set system 234
Dual shatter function 231
Duality of linear programming 223 (10.1.2)
Duality of planar graphs 82
Duality transform 80 (5.1.1) 83
Dvoretzky — Rogers lemma 326 (14.6.2) 329
Dvoretzky's theorem 325 (14.6.1) 329
E(G) (edge set) 12
Edge of an arrangement 51
Edge of arrangement 127
Edge of polytope 88
Edge, halving 252
Edges, pairwise crossing 169
Edges, parallel 169
Edmonds' matching polytope theorem 277
Efficient comparison theorem 286 (12.3.1)
Eigenvalue, second, of graph 347
Eigenvalue, second, of random graph 352
Elekes — Ronyai theorem 54
Elimination, Fourier — Motzkin 87
Ellipsoid method 352
Ellipsoid, almost spherical section 319 (14.4.1)
Ellipsoid, definition 306
Ellipsoid, Lowner — John 307
Ellipsoid, smallest enclosing, computation 307
Embedding into 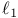 351 362 365 351 362 365
Embedding into 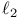 365 (Ex.4) 365 (Ex.4)
Embedding into 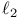 , algorithm 351 , algorithm 351
Embedding into 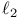 , dimension reduction 334 (15.2.1) , dimension reduction 334 (15.2.1)
Embedding into 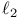 , lower bound 340 343 348 352 , lower bound 340 343 348 352
Embedding into 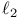 , testability 349 (15.5.2) , testability 349 (15.5.2)
Embedding into 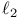 , upper bound 357 (15.7.1) , upper bound 357 (15.7.1)
Embedding into  352 352
Embedding into  , isometric 353 (Ex.4) 353 , isometric 353 (Ex.4) 353
Embedding into 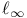 , isometric 354 (15.6.1) , isometric 354 (15.6.1)
Embedding into 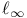 , upper bound 355 (15.6.2) , upper bound 355 (15.6.2)
Embedding into arbitrary normed space 341
Embedding of planar-graph metrics 360
Embedding of tree metrics 360 365 365 365
Embedding, distortion and dimension 341
| Embedding, distortion and dimension, lower bound 339 (15.3.3)
Embedding, isometric 332
Embedding, volume-respecting 362
Entropy (graph) 291
Envelope of segments 159
Envelope of segments, lower bound 163 (7.2.1)
Envelope of simplices 178
Envelope of triangles 175 (7.5.1) 178
Envelope, lower, of curves 160 179
Envelope, superimposed projections 184
Epsilon-net theorem 228 (10.2.4)
Epsilon-net theorem, application 235 239
Epsilon-net theorem, if and only if form 240
Equivalent polytopes, combinatorially 90 (5.3.4)
Equivalent radius 280
Erdos — Sachs construction 342 (Ex.1)
Erdos — Simonovits theorem 204 (9.2.2)
Erdos — Szekeres lemma 278 (Ex.4)
Erdos — Szekeres Theorem 40 (3.1.3)
Erdos — Szekeres theorem, application 44
Erdos — Szekeres theorem, generalizations 42
Erdos — Szekeres theorem, positive-fraction 211 (9.3.3) 213
Erdos — Szekeres theorem, quantitative bounds 42
Euler function 58
Excess 149
Excl(H) (excluded minor class) 360
Excluded minor, and metric 360
Expander 346
Expander, LPS 341
Exposed point 96 (Ex.8)
Extension of Lipschitz mapping 336
Extension, linear 285
Extremal point 88 96 96
Extreme (in arrangement) 141 (Ex.1)
f-vector 96
f-vector of representable complex 189
Face lattice 90
Face of arrangement 124 128
Face of polytope 88 (5.3.1)
Face, popular 146
Facet of arrangement 124
Facet of polytope 88
Facet, halving 252
Facet, halving, interleaving lemma 262 (11.3.1)
Facet, halving, interleaving lemma, application 263 268 271
Facet, k-facet 251
Factorization, of polynomial 36
Fano plane 51
Farkas lemma 19 19 20
Farthest-point Voronoi diagram 117
Fat objects, union complexity 185
Fat-lattice polytope 106 (Ex.1)
Finite projective plane 51 70
First selection lemma 200 (9.1.1)
First selection lemma, application 241
First selection lemma, proofs 202
Flag 104 127
Flat 14
Flattening lemma 334 (15.2.1)
Flattening lemma, application 340
Flipping (Delaunay triangulation) 118
Forbidden permutation 170
Forbidden short cycles 337
Forbidden subgraph 69
Forbidden subgraph and crossing number 62
Forbidden subhypergraph 204 (9.2.2)
Forbidden submatrix 170
Forbidden subsequence 168
Forest, regular 30 (2.1.2)
Form, linear 37 (Ex.4)
Four-square theorem, Lagrange's 38 (Ex.2.3.1)
Fourier — Motzkin elimination 87
Fraction, approximation by 32 (Ex.4) 32
Fractional Helly theorem 187 (8.1.1)
Fractional Helly theorem for line transversals 247 (10.6.2)
Fractional Helly theorem, application 200 203 245
Fractional packing 222
Fractional transversal 222
Fractional transversal for infinite systems 224
Fractional transversal, bound 244 (10.5.2)
Fractions, approximation by 31 (2.1.3)
Frechet's embedding 354
Freiman's theorem 54
Fueredi — Hajnal conjecture 170
Function, Ackermann 167
Function, convex 12
Function, dual shatter 231
Function, Euler's 58
Function, Lipschitz 316 317
Function, primitive recursive 167
Function, rational, on Cartesian product 55
Function, shatter 228
g(n) (number of distinct distances) 50
g-theorem 104
g-vector 104
Gale diagram 110
Gale transform 106
Gale transform, application 202 266
Gale's criterion 97 (5.4.4)
Gallai-type problem 221
Gallery, art 234 238
Gauss integers 58
Gaussian distribution 328
Gaussian measure 313
Gaussian measure concentration 314 (14.2.2)
General position 15
General position of convex sets 42
Generalized arithmetic progression 54
Generalized Davenport — Schinzel sequence 168 169
Generalized lower bound theorem 104
Generalized lower bound theorem, application 264
Generalized triangle 70 (4.5.3)
Genus, and VC-dimension 239 (Ex.6)
Geometric graph 61 169
Geometry of numbers 29 31
Geometry, real algebraic 129
girth 337
Girth and 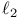 -embeddings 352 -embeddings 352
Goemans — Williamson algorithm for MAXCUT 353 (Ex.5)
Graded lattice 90
Graph 11
Graph drawing 60
Graph drawing, on grid 94
Graph drawing, rubber-band 93
Graph of polytope 89
Graph of polytope, connectivity 89 96
Graph of polytope, number of 135 (Ex.3)
Graph, 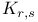 -free 69 72 -free 69 72
Graph, bipartite 12
Graph, comparability 278 (Ex.4) 291
Graph, complete 12
Graph, connected 12
Graph, determines a simple polytope 94
Graph, entropy 291
Graph, geometric 61 169
Graph, intersection 135 (Ex.2)
Graph, isomorphism 12
Graph, Moore 341
Graph, perfect 274—279
Graph, random, second eigenvalue 352
Graph, regular 12
Graph, shattering 239 (Ex.5)
Graph, without short cycles 337
Grassmanian 317
Greedy algorithm 225 225
Growth function see Shatter function
Gruenbaum — Motzkin conjecture 248
h(a) (height in poset) 287
H-polyhedron 84 (5.2.1)
H-polytope 84 (5.2.1)
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




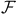 ) (VC-dimension)
) (VC-dimension) 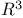
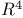
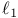

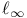 , isometric
, isometric 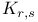 -free
-free