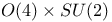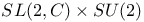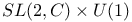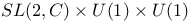Carmeli M. — Classical Fields: General Gravity and Gauge Theory :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Carmeli M. — Classical Fields: General Gravity and Gauge Theory

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Classical Fields: General Gravity and Gauge Theory

Автор: Carmeli M.

Аннотация:

This textbook for a one-year graduate course in theoretical physics explores the classical theory of fields with a mix of electrodynamics, gauge fields, and gravitation. Carmell (Ben Gurion) develops the geometry of curved spacetime, the Einstein field equations, gravitational fields of elementary mass systems, the equations of motion in general relativity, spinor formulation of gravitation and gauge fields, and the gauge theory of gravitation.

Язык:

Рубрика: Физика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Год издания: 1982

Количество страниц: 650

Добавлена в каталог: 09.06.2006

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

Gravitational energy      200
Gravitational field      1—19
Gravitational field of body with quadrupole structure      177—182
Gravitational field of spherically symmetric charged body      168—171
Gravitational field with quadrupole moment      177—182
Gravitational field with rotational symmetry      172 177
Gravitational field, action integral for      93—105
Gravitational field, basic properties of      10—13
Gravitational field, classification of      130 488—509
Gravitational field, combined with electromagnetic field      580—590
Gravitational field, deflection of light m      222—226
Gravitational field, delay of radar pulses in      227—230
Gravitational field, eigenspinor-eigenvalue equation of      500—507
Gravitational field, equations      84—88
Gravitational field, equations, derivation of      84 86
Gravitational field, equations, Newtonian limit of      88—93
Gravitational field, equations, pure      583—586
Gravitational field, equations, tetrad formulation of      135—143
Gravitational field, external      267—268
Gravitational field, invariants of      492—499
Gravitational field, motion in centrally symmetric      215—222
Gravitational field, properties of      205—265
Gravitational field, spinors      434—445 467
Gravitational field, stationary and static      130—134
Gravitational field, weak      205—213 242 251
Gravitational fields of elementary mass systems      155—204
Gravitational Lagrangian      94 98
Gravitational lime dilation      214
Gravitational mass      4 13—16 299
Gravitational potential      227
Gravitational principal null directions      493
Gravitational radiation      234—246 278 494 506
Gravitational radiation from isolated system      251—253 254
Gravitational radiation from solar system      259—262
Gravitational radiation in nonrelativistic collisions      257—259
Gravitational radiation in slow motion      278—279
Gravitational radiation, power formula      261
Gravitational red shift      213—215
Gravitational spinor      436—438
Gravitational waves      234 235 242—244 251 252 403
Gravitational waves, cylindrical      198—199 235
Gravitational waves, detection of      227
Gravitational waves, helicity and polarization of      243—244
Green's formula      301
Green's function      279
Group velocity      401 402
Group, 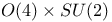$O(4)\times SU(2)$       472
Group, 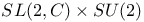$SL(2,C)\times SU(2)$       593—595
Group, 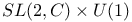$SL(2,C)\times U(1)$       555 580 586 587 590
Group, 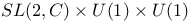$SL(2,C)\times U(1)\times U(1)$       590—593
Group, 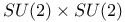$SU(2)\times SU(2)$       471—480
Group, 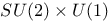$SU(2)\times U(1)$       509 580
Group, abelian      560
Group, Bondi — Metzner — Sachs      242
Group, compact      445
Group, conformal Kale      563
Group, covariance      388—389
Group, covering      416 445
Group, euclidean      128 129
Group, Galilean      1—2
Group, gauge      470 560
Group, Gl(2,C)      562 563
Group, GL(n,R)      551
Group, infinite parameter      242
Group, inhomogeneous Lorentz      124
Group, Klein      497
Group, Lie      470 562
Group, Lorentz      13 149 416 456 462 472 491 626
Group, non-abelian      560
Group, O(2,C)      563
Group, O(3)      445
Group, O(4)      471—480
Group, phase      563
Group, Poincare      13 123—128 207 243 349 350 358
Group, SL(2,C)      149 397 407—413 415 416 455—463 472 476 491 509 554
Group, special linear      388
Group, structure      562
Group, SU(1,1)      388
Group, SU(2)      445 447 471—480 509
Group, SU(3)      509
Group, SU(4)      509
Group, U(1)      553 560
Group, unitary      560
Group-theoretical interpretation      331
Gyroscope      322 626
Hamilton — Jacobi equation      67 154
Hamiltonian      578
Hankel function      9 10
Harmonic coordinate system      152 281 296 300 301
Harmonic function      175 275 370
Hartle, J.B.      404 405
Hausdorff manifold      555
Havas, P.      281 363
Hawking, S.W.      404 403 616
Hayashi, M.J.      615
Haystack radar      230
Helicity and polarization of gravitational waves      243—244
Herit, E.      405
Hermitian scalar product      388
Hiawka, E.      616
Hicks, N.J.      616
Higgs symmetry-breaking phenomenon      610
Hirzebruch, F.      551
Hoffmann, B.      277 296 322 363
Hojman, S.      326 361 363
Holonomic basis      556
Horizon      401 402 404
Horizontal and vertical covariant derivatives      620—623
Hughston's criterion      390
Hughston, L.P.      390 405
Husemoiler D.      616
Hydrodynamics      206
ICARUS      221
Identities, Bianchi      80—82 139-141 296 432—433 442 568 570
Identities, contracted      81—82 85
Identities, differential      80—83
Identities, Ricci      69—70
Identities, Spinorial Ricci      430
Indices (dotted, primed, undotted, unprimed)      411 413 416 419
Indices (dotted, primed, undotted, unprimed), SU(2) spinor      445 454 455
Inequivalent realization      517
Inertial force      11
Inertial mass      4 13—16 281 299
Inertial system of coordinates      1 2 12
Infeld, L.      267 277 296 297 299 322 363 416
Infinite parameter group      242
Infinitesimal generators      124 447 472
Infinitesimal mapping      113
Infinitesimal matrices      125
Infinitesimal transformation      113 122
infinity      235 240
Ingalls, R.P.      265
Inhomo eneous Lorentz group      124 242
Initial data      238 241
Initial-value problem      152—154 241
Inner planet      227
Inner produce      557
Integrals of motion      343—363
Integrals of motion, Wigner — Lubanski      334—336 346 349 350 358
Internal basis      446
Internal space      445 554
Internal symmetry      560
Intrinsic derivative      137 571
Invariant voluma element      36
Invariants      22
Invariants in presence of electromagnetic field      499—500
Invariants of electromagnetic field      481—484
Invariants of gravitational field      492—499
Invariants of gravitational field in presence of electromagnetic field      499—500
Invariants of Yang — Mills field      509—511 516

Inverse metric      186
Inverse-square law      10
Ipser, R.J.      143 396 403
Irreducible components      73
Irreducible quantity      30
Isaacson stress-energy tensor      403
Isometric mapping      123
Isospin      449—450 454 471 560
Isospin space      448
Isospinor      454
Isotopic spin, gauge theory      560
Isotopic spin, transformation      560
Isotriplet      449
Isotropic Cartesian coordinates      162
Isotropic spherical coordinates      162 230
Isovector      454
Israel theorem      366
Israel, W.      366 405
Jackiw, R.      472 479 480
Jacobian      21 22 35 121 555
Janis, A.I.      601
Jupiter-Sun system      262
Jurgens, R.P.      265
Kaluza, T.      579
Kasner, E.      163
Kaye, M.      135 154 185 204 336 363 389 405 480 507 543 562 616
Kerr black hole      405
Kerr coordinates      400 402
Kerr metric      131 144 185 323 366 382—383 384 386 387 389—404
Kerr metric, generalized      391
Kerr metric, nonstationary      389—396
Kerr metric, perturbation on      396—409
Kerr metric, radiative      390—391
Kerr metric, source of      391
Kerr metric, variable-mass      391 507
Kerr — Newman metric      608 610
Kerr — Schild metric      390
Kerr, R.P.      366 382 389 403
Kerr-type geometry      612
Killing equation      122—130
Killing vector      123 172 327 360 361 390
kinetic energy      280 299
Kinnersley, W.      186 388 405
Klein four-group      497
Klein — Gordon equation      102 103
Klein's bottle      237
Klein, O.      579
Kniskal, M.D.      165 204
Kobayashi, S.      616
Kramer, D.      405
Kronecker delta      22 26
Kronecker delta, covariant derivative of      56
Kronecker delta, generalization of      31
Krotkov, R.      14
Kruskal coordinates      163—166
Kruskal diagram      167
Kruskal manifold      165
Kugler, M.      552
Lagrange equation      62 576
Lagrangian desity for Lewis line element      369
Lagrangian desity for rotator      366
Lagrangian desity for scalar field      102
Lagrangian desity for SL(2,C) theory      568 570 572—579 585—586 589 591—592
Lagrangian desity for Yang — Mills theory      448 449
Lagrangian for Einstein — Infeld — Hoffmann equation      321
Lagrangian for electromagnetic field      100
Lagrangian for gravitational field      94 98
Lagrangian for motion in Schwarzschild field      232
Lagrangian, Einstein      312
Lagrangian, post-Newtonian      316—322
Landau — Lifshitz pseudotensor      248—249
Landau, L.D.      92 247 264 265
Laplace equation      3 7—10 175 176 210 377
Laplacian operator      3 91 370 372 376 377
Left dual      71
Legendre equation      377
Legendre function      179
Legendre polynomials      6 179 377
Lemaitre, G.      163
Levi-Civita tensor densities      37—45 422 423 426
Levi-Civita tensor densities, covariant derivative of      59
Levi-Civita, metric spinors      416 417 420
Levi-Civita, T.      51 172 366 405
Lewis line element      368
Lewis, T.      366 405
Lie derivative      113—122 622
Lie group      470 562
Lie group, representation of      552
Lifshitz, E.M.      92 247 264 265
Light cone      209 235 419 458 459 602
Light cone at infinity      235
Lindquist, R.W.      336 337 363 405
Line element      33
Line element, general form of      366—367
Line element, Lewis      368
Line, geodesic      64 163
Linear approximation      206—207
Linear momentum      329
Linear representation      409
Linear space      409
Linearized Einstein equations      207—213 234 242 251 403
Local coordinate system      557
Local SU(2) transformation      446—447
Loos, H.      480
Lorentz force law      87
Lorentz group      13 149 416 456 462 472 491 626
Lorentz group, inhomogeneous      124 242
Lorentz group, representation of      455—463 491
Lorentz invariant versus gauge invariant methods of classification      530—532
Lorentz matrices      126
Lorentz transformation      12 20 127 129 130 270 455 482 483 497
MacCallum, M.      405
Macfarlane, a.j.      404
MacKenzle, K.      616
Magnetic mom poles      590—593
Malm, S.      ix 480 601 616
Mandlestam, S.      578
Manifold, compact conformal      235
Manifold, complete      165
Manifold, curvature forms of      551
Manifold, Hausdorff      555
Manifold, Kruskal      165
Manifold, maximal      165
Manifold, orientable      237
Mapping      367 380 381 383 385 387
Mapping, conformal      74 470
Mapping, infinitesimal      113
Mapping, isometric      123
MARS      221
Martellini, M.      578 579 616
Mass center in general relativity      623—630
Mass center in general relativity, characterization of      626—628
Mass multipole      180
Mass particle in gravitational field      268—270
Mass quadrapole moment tensor      5 7 253 256
Mass, effective      330
Mass, gravitational      4 13—16 299
Mass, inertial      4 13—16 281 299
Mass, proper      282
Mass, rest      243
Master equation      144
Mathematical techniques      618—623
Matrices, Dirac      473
Matrices, Pauli      416 418 447 449 454 455
Matrices, s $\mu$       472—476
Matrices, spin      474
Matrix method of classification - a four-way scheme      532—552
Matrix method of classification of SU(2) gauge fields      517—529
Maximal extension of Schwarzschild metric      165—168
Maximal manifold      165

1 2 3 4 5 6

О проекте