|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Carmeli M. Ч Classical Fields: General Gravity and Gauge Theory |
|
|
 |
| ѕредметный указатель |
"Tail" (of radiation) 201 203 255
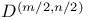 (spinor representation) 411 (spinor representation) 411
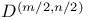 (spinor representation), particular cases of 413 415 (spinor representation), particular cases of 413 415
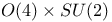 (group) 472 (group) 472
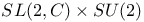 (group) 593Ч595 (group) 593Ч595
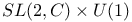 (group) 555 580 586 587 590 (group) 555 580 586 587 590
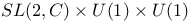 (group) 590Ч593 (group) 590Ч593
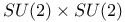 (group) 471Ч480 (group) 471Ч480
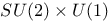 (group) 309 580 (group) 309 580
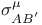 (matrices) 416 420 421 434 (matrices) 416 420 421 434
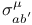 (null tetrad matrices 568 570 571 572Ч578 586 587 (null tetrad matrices 568 570 571 572Ч578 586 587
't Hooft, G. 578
Abelian gauge fields 559Ч560
Abelian gauge theory 560
Abelian group 560
Abelian solutions of Yang Ч Mills theory 600Ч601
Action functional 310
Action integral for gravitational field 93Ч105
Action principle 310Ч311
Action-at-a-distance 3 313
Adapted coordinate system 131 172
Advanced time 279
Affine connection 46 424 426 471 567
Affine connection, spinor 419 420 424 426 566 567
Affine connection, torsion-free 551
Affine parameter 64Ч65
Algebra of the matrices 472Ч476
Algebraically special solution 389 390
Anandan, J. 552
Angle of deflection of light 224
Angle of deflection of light, Newtonian calculation of 225Ч226
Angles Euler 445
Angular velocity 212 213
Anholonomic basis 556
Anticommutation relation 473
Antisymmetric tensor 26
Antisymmetrization 28
Aperiodic solution 200
Arecibo Ionospheric Observatory 229
Ash, M.E. 265
Asymptotic flatness 239 240
Atlas 555
atomic clocks 214
Auslander, L. 616
Axisymmetric solutions of Einstein field equations 365Ч406
Bardeen, J.M. 144
Base space 562
Bases 556
Basis spinor 445 446
Basis vectors 556
Basombrio, F.G. 616
Batygin, V.V. 264
Bazanski, S. 310 363
Beiglboeck, W. 627 628 630 630
Bel, L. 405
Bertotti, B. 281 363
Bessel equation 8 10
Bessel function 8 9 199
Bessel, F.W. 13 14
Bianchi identities 80Ч82 139Ч141 296 432Ч433 442 568 570 614
Bianchi identities for coupled gravitation and gauge fields 594
Bianchi identities for gauge fields 448
Bianchi identities, contracted 81Ч82 85 266
Bianchi identities, spin-coefficient form of 137
Bijection 555
Binary star 262
Birkhoff theorem 160
Bisurface 172 367
Bjorken, J.D. 19
Black hole 401 404 610
Boltzmann's constant 259
Bondi coordinates 244Ч246
Bondi news function 241
Bondi Ч Metzner Ч Sachs group 242
Bonnor, W.B. 281
Boost 457 458
Borel, A. 551
boundary conditions 400Ч401
Boyer, R.H. 405
Boyer-I indquist coordinates 383 387 396 400 402
Braginsky, V.B. 14 19
Brehme, R.W. 618Ч630
Bremsstrahlung, gravitational 255Ч265
Brocket man, R.A. 265
Bruhat, Y. 154
Bundle space 559 562
C-invariance 555
Campbell, D.B. 265
Canonical cylindrical coordinates 175 370 371 380
Canonical form 515Ч516
Canonical spheroidal coordinates 363
Carmeli, M. 19 135 154 204 230 259 260 265 280 331 336 363 389 404 405 514 517 543 551 552 554 562 570 607 612 616
Carmell classification scheme 509Ч516 530Ч532 533
Cartan, E. 408 480
Carter, B. 366 405
Cartesian coordinates 11 33 113 161 206 224 421 558
Cartesian coordinates, isotropic 162
Cartesian product bundle 559
Casimir operator 334 346 348 350 358
Castillejo, L. 552
Cauchy problem 152 153
Caustic surface 192
Center of mass 618 628
Centrifugal force 14Ч16
Change of basis for spinors 461 463
Charach, Ch. 331 336 363 480 543 616
Characterization of mass center 626Ч628
Chart 555
Chern classes 530Ч352
Chern polynomial 551
Chern, S.S. 551
Cho, Y.M. 552
Choice of coordinate system 244Ч246 270Ч271
Christoffel symbols 45Ч51 424 426 471
Christoffel symbols, transformation laws of 46Ч48
Classical fields vii 267 310
Classical mechanics 1
Classification by spinor method 500Ч507
Classification of electromagnetic field 481Ч488 517Ч520
Classification of electromagnetic field, diagram of 485
Classification of gauge fields, diagram of 514
Classification of gauge fields, eigenspinor-eigenvalue equation of 509Ч516
Classification of gauge fields, four-way scheme of 532Ч552
Classification of gauge fields, Lorentz invariant versus gauge invariant methods 530Ч532
Classification of gauge fields, matrix method 517Ч529
Classification of gravitational and gauge fields 481Ч552
Classification of gravitational field 130 488Ч509
Classification of gravitational field, diagram of 503 505
Classification of gravitational field, eigenspinor-eigenvalue equation of 500Ч507
Classification of Weyl tensor 490Ч492
Classification of Weyl tensor, eigenvector-eigenvalue equation of 490
Classification, Carmeli 509Ч516 530Ч532 533
Classification, Penrose 492Ч507
Classification, Petrov 488Ч492 507 509
Classification, Wang Ч Yang 514 517Ч529 530Ч532 534
clocks 213 214
Collapse 198
Collapsed object 365
Collapsed rotating object 366
Collapsing matter 189
Collision 255
Combined gravitational and electromagnetic fields 586Ч590
Commutation coefficients 556
Commutator 68 421 446 556
Commutator equations 137
Commutator operator 421 429 433
Comoving coordinates 190Ч192
Compact group 445
Complete manifold 165
Complex conjugate bundle 563 564
| Complex potential 388
Complex rotation 482 491
Complex vector bundle 559 562
Complexification isomorphism 561
components 22
components of vector 22
Components, irreducible 73
Conformal mapping 74
Conformal mapping of gauge fields 470
Conformal scale group 563
Conformal space 73
Conformal spinor 437 439Ч442 467
Conformal structure of spacetime 235Ч239
Conformal tensor 72Ч76 237 238 367 464
Conformal transformation 235 237 239 242
Conformal transformation, properties of 73Ч76
Conformally fiat space 172
Connected manifold 555
Connection 557 558
Conservation law of angular momentum 250
Conservation laws in presence of gravitation 247Ч248 250
Conservation of isospin 449Ч450
Conserved currents 599
Constant of motion 624
Constant-phase solution to Ernst equation 382
Contracted Bianchi identities 81Ч82
Contraction 25 417
Contravariant tensor 23
Contravariant vector 22 556
Coordinate basis 556
Coordinate conditions 151Ч152
Coordinate conditions, deDonder 152 281 296 300 301
Coordinate singularity 165
Coordinate system, Fermi 51 270 558
coordinates 20Ч22
Coordinates, adapted 131 172
Coordinates, Bondi 244Ч246
Coordinates, Boyer Ч Lindquist 383 387 396 400 402
Coordinates, canonical cylindrical 175 370 371 380
Coordinates, canonical spheroidal 383
Coordinates, Cartesian 11 33 113 161 206 224 421 558
Coordinates, choice of 244Ч246 270Ч271
Coordinates, comoving 190Ч912
Coordinates, curvilinear 12
Coordinates, cylindrical 7Ч10 175 370
Coordinates, ellipsoidal 177
Coordinates, Fermi 51 270 558
Coordinates, freely falling 11
Coordinates, geodesic 50 82 247 248
Coordinates, harmonic 152 281 296 300 301
Coordinates, inertial 1 2 12
Coordinates, isotropic Cartesian 162
Coordinates, isotropic spherical 162 230
Coordinates, Kerr 400 402
Coordinates, Kruskal 163Ч168
Coordinates, local 557
Coordinates, noninertial 11 12
Coordinates, null 183 337 459
Coordinates, prolate spheroidal 177 181 375 379
Coordinates, retarded time 337 343 389 390 391 459
Coordinates, rotating 12
Coordinates, spherical 381
Coordinates, spheroidal 377 389
Coordinates, transformation of 20Ч23 113 172 276
Corinaldesi Ч Papapetrou supplementary condition 326 331Ч334 338 360
Corinaldesi, E. 322 326 328 331 363
Coriolis force 212
Correspondence between spinors and tensors 416Ч419
Cosmological constant 87 240 467
Cotangent space 557
Coulomb collision 255
Coupling matter and gauge fields 569Ч571
Covariance group of Ernst equation 388Ч389
Covariant derivative 53 557 618
Covariant derivative of spinor 419Ч421
Covariant derivative operator 420 421 557
Covariant derivative, double 471 593Ч594
Covariant derivative, gauge 447Ч448
Covariant derivative, horizontal 620Ч623
Covariant derivative, vertical 620Ч623
Covariant differentiation 51Ч61 557 618
Covariant differentiation, rules for 55Ч58
Covariant tensor 23
Covariant vector space 556
Covariant vectors 23 557
Covering group 416 445
CPT-invariance 555
Crammer, J. 267 322 363
Cranshaw, T.F. 214 215
Cross section 495 562
Curl 141 373
Current vector 107 111 142 312
Curvature spinor 428Ч434
Curvature spinor, spinor equivalent of 434Ч435
Curvature spinor, symmetry of 430Ч431
Curvature tensor 67Ч80 237 428 429 431 432 434Ч435 464 465
Curvature tensor, symmetry of 70Ч71
Curvature, Gaussian 76
Curvature, mean 76
Curvature, scalar 238
Curve, null 66
Curved spacetime 13 20 415 416
Curved spacetime, geometry of 20Ч83
Curvilinear coordinates 12
Curzon metric 380
Curzon, H.E.J. 381
Cylindrical coordinates 7Ч10 175 370 380
Cylindrical gravitational waves 198Ч199 235
D'Alembertian operator 208 242 278
D(g) (operator) 409
Debever Ч Penrose equation 492
Debye shielding radius 259
Decomposition of Riemann tensor 78 434Ч435 443
Decoupled electromagnetic equations 147Ч148
Decoupled gravitational equations 144Ч147
DeDonder coordinate condition 152 281 296 300 301
Deflection of light in a gravitational field 222Ч226 234
Deformation parameter 384
Delay of radar pulses in gravitational field 227Ч230
Delay of radar pulses in gravitational field, angle of 224
Delta, covariant derivative of 56
Delta, Dirac 111 201
Delta, generalization of 31
Delta, Kronecker 22 26
Demianski Ч Newman metric 386Ч387
Demianski, M. 366 386 405
Densities, Levi-Civita 37Ч38 422 423
Densities, scalar 35
Densities, tensor 35Ч45
Densities, vector 35
Densities, weight of tensor 35
Derivative, covariant 51Ч61 557 618
Derivative, directional 186 392 555 571 602
Derivative, double covariant 471
Derivative, gauge covariant 447Ч448
Derivative, intrinsic 137 571
Derivative, Lie 113Ч122 622
Detection of gravitational waves 227
DeWitt, B.S. 618 630
Diagram of classification, of electromagnetic field 485
Diagram of classification, of gauge field 514
Diagram of classification, of gravitational field 503 505
Diagram, Kruskal 167
Diagram, Penrose 236 237 240 503 505
Dicke, R.H. 14 16 19 299
Differentiable manifold 555
Differential forms 161
Differential geometrical analysis 553Ч558
Differential geometry, an introduction 555Ч558
Differential geometry, an introduction, general relativistic interpretation of 558Ч559
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



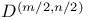 (spinor representation)
(spinor representation) 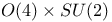 (group)
(group) 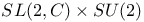 (group)
(group) 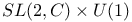 (group)
(group) 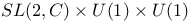 (group)
(group) 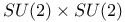 (group)
(group) 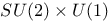 (group)
(group) 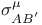 (matrices)
(matrices) 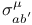 (null tetrad matrices
(null tetrad matrices