|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grotschel M., Lovasz L., Schrijver A. — Geometric Algorithms and Combinatorial Optimization |
|
|
 |
| Предметный указатель |
 -polar 180 -polar 180
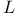 -perfect graph 299 -perfect graph 299
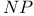 -complete 28 29 -complete 28 29
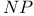 -easy 29 -easy 29
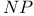 -equivalent 29 -equivalent 29
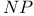 -hard 29 -hard 29
(Hitchcock-Koopmans) transportation problem 232
(r, s)-dicut 239
(r,s)-cut 198
(s, t)-cut 19
(s, t)-diwalk 19
Absolute error 34
Acyclic digraph 20
Acyclic subgraph problem 253
Adjacency on a polyhedon 183
Adjacent 17
Adleman, L. 221 331
Affine combination 3
Affine hull 3 182—184
Affine rank 3
Affine subspace 3
Affinely (in)dependent 3
Agmon, S. 35
Aho, A.V. 21 331
Akguel, M. 282 342
Algorithm 22 22—23
Almost bipartite graph 274
Antiblocker (of a convex set) 11 130—131 188 283
Antiblocker (of a hypergraphl 284
Antidominant 11
Apery, R. 35 343
Approximation of numbers 29—36
Approximation problem, best 134 137
Approximation problem, diophantine 133—156 134 168—170
Approximation problem, simultaneous diophantine 138 138—139 146—156 168—170
Arborescence 20 201—203 218 242 242—247
Arborescence packing problem 246
Arborescence, rooted 20 201 242
ARC 18
Arithmetic model 32
Assignment problem, optimal 232 232—233
Avi-Itzhak, B. 332
b-matching 46 257 250—259 265
b-matching polytope 257
Babai, L. 149 195 331
Bachere, A. 45 150 339 341
Balas, E. 301 302 331
Balinski, M.L. 233 331
Ball of radius  around K 6 around K 6
Ball of radius  with center a 6 with center a 6
Barahona, K 249 250 254 262 331
Barany, I. 127 331
Basic ellipsoid method 73—86 75
Basic feasible index set 41
Basic feasible solution 10
Basic optimum dual solution of a linear program 185
Basic solution 10
Basis 9
Basis of a lattice 139
Basis of a set in a matroid 211
Basis reduction 139—156 220
Basis, reduced 142 142—146
Beginning state 22
Beineke, L.W. 341
Bellman, R. 337 339
Berge, C. 16 255 256 277 279 280 282 283 331 332 344
Berkowitz, S.J. 40 332
Best approximation problem 134 137
Betke, U. 66 332
Binary search method 28
Bipartite graph 18 200 204 208—210 229—233 273—274 279 305
Bipartite planar graph, nearly 274 274—275
Bipartition 18
Bixby, R.E. vii 211 332
Bland, R.E. 42 65 71 72 82 94 107 248 282 332
Block 19
Blocker of a hypergraph 225 225—229
Blocker of a set 11 130—131 188 225—229
Blow-up parameter 82
Bock, F. 242 332
Boland, J.Ch. 280 341
Bollobas, B. 16 332
Bondy, J.A. 16 332
Bonnesen, T. 49 332
Booth, K.S. 280 332
Borfivka, O. 247 332
Borgwardt, K.H. 42 64 332
Bose, R.C. 336
Boulala, M. 274 332
Bounded set 9
Branching 20 245 245—247
Brickell, E.F. 221 332
Bridge 19
Burlet, M. 281 332
Cactus 274
Capacitated (Hitchcock — Koopmans) transportation problem 232
Capacitated b-matching 258
Capacitated spanning tree packing problem 251
Capacitated weighted (perfect) b-matching problem 258
Caratheodory's theorem 10
Caratheodory, C. 10 162 184
Cassels, J.W.S. 139 332
Cauchy — Schwarz inequality 8
CEILING 2
Center of a wheel 300
Center of an ellipsoid 67
Centered convex set 53
Central cut 72
Central-cut ellipsoid method 86—94 87
Centrally symmetric parallel cuts 72
Centrally symmetric set 123
Characteristic polynomial 4
Cheriton, D. 247 332
Cheung, T-Y. 236 333
Chinese postman problem 262
Chord 19
Chordal graph 280
Chromatic index 208
Chu, Y.J. 201 242 333
Chvattal, V. 1 13 273 274 281 282 302 332 333
Circuit 19
Circuit problem 21
Circuit, odd 19 272—276
Circuit-constrained stable set polytope 275
Circulation 241
Circumscribed convex set 53
Claw 18
Claw-free graph 302
CLIQUE 18 229 272—303
Clique constraint 276 276—298
Clique covering 18
Clique covering number 229 277—279 296—298
Clique number 229
Clique tree 264 264—265
Clique tree inequality 265
Clique-constrained stable set polytope 283
Closed walk 20
Clutter 225
Color classes 18
Coloring 18
Coloring number 229 277—279 296—298
Coloring, edge 208—210 229
Column sum norm 7
Column vector 1
Combination , conic 3
Combination, affine 3
Combination, convex 3
Combination, linear 3
Combination, proper 3
Commodity 266
| Comparability graph 280
Compatible norm 7
Complement of a graph 18
Complementary problem 25
Complementary slackness theorem 15
Complete bipartite graph 18
Complete graph 18
Complexity theory 21—36
Complexity, space 23—24
Complexity, time 23—24
Component of a graph 19
Cone 3
Conformal clutter 284
Conforti, M. 262
Conic combination 3
Conic hull 3
Connected graph 19
Connected nodes 19
Continued fraction 134—137 135
Continued fraction expansion 135
Contraction in a graph 17
Contraction in a matroid 212
Convergent 135
Convex body 53
Convex combination 3
Convex function 49 55—56 188
Convex function minimization problem 55 56
Convex hull 3
Convex set 3 46—132
Cook, S.A. 28 333
Cook, W. 259 333
Cornuejols, G. 265 333
Courant, R. 339
Cramer, G. 76
Cross-free 323
Crossing family 315 315—324
Crossing of two sets 244 323
Crowder, H. 46 265 333
Crypto-analysis 221
Cunningham, W.H. 46 214 256 257 258 282 310 311 333
Cut 17 198 201 247—254
Cut polytope 248—249
Cut, directed 19 239 251 251—254 321
Cut, odd 205 207—208 256 256—257 329
Cut, rooted 19 197—203 201 242—247 251—254 305
Cut, separating r from s 197—201 198 237—242 248—252
Cycle, even 236
Cycle, odd 235—236
D-simplex 10
Dantzig, G.B. 1 41 333 334 336
Danzer, L. 69 333
Decision problem 24
Deep cut 72
Deep-cut ellipsoid method 83
Degree 17 18
Deletion in a matroid 212
Deletion of a node set 17
Deletion of an edge set 17
Determinant 2 3031 40
Diameter 6 126
Diconnected digraph 19
Dicut 19 239 251 251—254 321
Dicut covering 251 251—254 321
Dicut packing problem 251
Dicycle 19
Digraph 18 18—20
Dijkstra, E.W. 235 247 333
Dijoin 251 251—254 321
Dijoin packing problem 251
Dilatation parameter 82
Dilworth truncation 320
Dilworth's Theorem 240
Dilworth, R.P. 240 277 280 304 320 333
DIMENSION 3
Dinits, E.A. 198 236 333
Diophantine approximation problem 133—156 134 168—170
Diophantine approximation problem, simultaneous 138 138—139 146—156 168—170
Diophantine equations, linear 11—12 45 155—156
Diophantine inequalities problem, linear 11—14 192 192—196
Dipath 19
Dipath, longest 240
Dipath, shortest 234—236
Dirac, G.A. 274 280 281 333
Directed cut 19 239 251 251—254 321
Directed cycle 19
Directed cycle packing problem 254
Directed graph 18
Directed path 19
Directed walk 19
Dirichlet, G.L. 134 138 139 141 146 334
Distance 5
Diwalk 19
Domich, P.D. 45 334
Dominant 11 226
Dorfman, Y.G. 250 343
Down-monotone 11
Dual basis of a lattice 151
Dual lattice 150
Dual program 15
Dual solution 185 185—188 189—192
Duality theorem 15
Duality, linear programming 15
Duchet, P. 282 332
Duffin, R.J. 274 334
Ecker, J.G. 64 334
EDGE 17
Edge coloring 208 208—210 229
Edge coloring number 208 230
Edge covering 229 229—233 259
Edge covering number 229
Edge covering polytope 259
Edge of a hypergraph 225
Edmonds' disjoint arborescence theorem 246
Edmonds' perfect matching polytope theorem 205
Edmonds, J. 16 25 37 39 46 160 181 189 201 202 204 205 206 213 214 216 238 242 244 245 246 250 255 256 257 258 260 261 262 282 304 306 308 312 313 316 319 320 321 322 333 334 344
Egervary, E. 200 231 232 334
Eigenvalue 4
Eigenvector 4
Elekes, G. 127 334
Elementary arithmetic operation 32
Elementary column operation 43
Elias, P. 199 335
Elimination, Gaussian 36—40
Ellipsoid 66 66—72
Ellipsoid method 64 64—101
Ellipsoid method, basic 73—86
Ellipsoid method, central-cut 86—94
Ellipsoid method, shallow-cut 94—101
Ellipsoidal norm 5
Emde Boas, P. van 141 335
Encoding 23
Encoding length 23 29—31 30 32
Encoding length of a convex set 54
Encoding length of a lattice 151
Encoding length of a linear program 30
Encoding length of a number 30
Encoding length of a polyhedron 136
Encoding length of an inequality (system) 30
Encoding scheme 22 23
end state 22
Endnode 17 19
Equations, linear 11—12 36—40
Equations, linear diophantine 11—12 45 155—156
Euclidean distance 5
Euclidean norm 5
Euler, L. 343
Eulerian digraph 19
Eulerian ditrail 19
Eulerian graph 19
Eulerian tour 19
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -polar
-polar 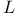 -perfect graph
-perfect graph 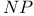 -complete
-complete  around K
around K