|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grotschel M., Lovasz L., Schrijver A. Ч Geometric Algorithms and Combinatorial Optimization |
|
|
 |
| ѕредметный указатель |
Minimization of a submodular function 310 310Ч311 315 316 325Ч329
Minimum (r, s)-cut problem 237
Minimum (r, s)-flow problem 239
Minimum basis problem 140
Minimum cut problem 247 248
Minimum degree 230
Minimum dicut problem 251
Minimum dijoin problem 251
Minimum feedback arc set problem 253
Minimum multicommodity cut problem 267
Minimum odd cut problem 257
Minimum potential problem 240
Minimum rooted cut problem 245
Minimum spanning tree problem 247
Minimum strongly connected subdigraph problem 247
Minimum weighted clique covering problem 296 296Ч298
Minimum weighted coloring problem 296 296Ч298
Minimum weighted perfect matching problem 204
Minimum weighted T-cut problem 207 258
Minimum weighted T-join problem 260
Minimum-cost circulation problem 241
Minimum-cost flow problem 238 238Ч242
Minkowski, H. v 131 140 141 148
Minty, G.J. 42 64 238 241 282 302 340 342
Moore, E.F. 235 342
Moser, J. 339
Mote, J. 236 337
Motzkin, T.S. 35
Multicommodity cut 267
Multicommodity cut packing problem 267
Multicommodity flow problem 266 266Ч271
Multicommodity path 267
Multiterminal flow problem 249
Munkres, J. 233 342
Murphy, F. 332
Murray, W. 66 337
Murty, U.S.R. 16 332
Name of a convex set 53
Named convex set 53
Nash-Williams, C.St. J.A. 251 335 342
Nearest lattice vector problem 141
Nearly bipartite planar graph 274
Neighbor 17
Nemchinov, V.S. 346
Nemhauser, G.L. 282 301 302 311 339 342
Nemirovskii, A.S. v 65 94 104 107 113 346
Nesetril, J. 302 331
Network flow problem 190Ч201 233Ч242 234
Network synthesis problem 248
Niven, I. 134 342
Node 17 18
Node covering 229 229Ч233
Node covering number 229
Node of a hypergraph 225
Nondeterministic polynomial time algorithm 24Ч26 25 56Ч63
Nonemptiness problem, strong 47 47Ч48 75 171 173Ч178
Nonemptiness problem, weak 51 51Ч53 171
Nonsingular matrix 3
Nonweiler, T.R.F. 134 343
Norm 5 5Ч8 125Ч126 148
Normal form, Hermite 43Ч45 155Ч156
Objective function 15
Odd antihole inequality 301
Odd circuit 19 272Ч276
Odd circuit constraints 273
Odd cut 205 207Ч208 256 256Ч257 329
Odd cut constraints 205
Odd cycle 235Ч236
Odd submodular function minimization 325Ч329
Odd wheel constraints 300 300Ч301
Odlyzko, A.M. 149 218 220 221 341 343
Okamura, H. 268 343
Olaru, E. 281
Optimal assignment problem 232 232Ч233
Optimal solution 15
Optimization oracle 55
Optimization over extended polymatroids 309
Optimization over intersections of extended polymatroids 310
Optimization over potymatroids 309
Optimization problem, strong 47 47Ч50 162Ч163 171Ч172 179Ч180 191Ч192
Optimization problem, weak 50 50Ч53 102Ч122 170Ч174 173
Optimum dual solution 185 185Ч188 189Ч192
Oracle 26Ч29 27
Oracle algorithm 26
Oracle tape 26
Oracle-polynomial time algorithm 27 54
Orden, A. 238 343
Order of a graph 17
Ore, O. 255 343
Origin 19
Orlin, J.B. 238 343
Orlova, G.I. 250 343
Orthogonal 8
Orthogonalization, Gram Ч Schmidt 40
Orthonormal representation 285 285Ч296
Orthonormal representation constraint 285
Outdegree 18
Outer radius 53
Output of a problem 22
Padberg, M.W. vii 46 65 207 217 223 257 258 259 263 265 301 331 333 338 343
Papadimitriou, C.H. vii 65 236 239 262 265 267 339 343
Parallel cuts 72
Parallel edges 17
Parallelepiped 8
Parity graph 281
Parthasarathy Ч Ravindra graph 282
Parthasarathy, K.R. 282 343
Partially ordered set 240Ч241 280
Partition mattold 211
Path 19
Pentagon 19
Perfect b-matching 257
Perfect b-matching polytope 257
Perfect graph 276 276--298
Perfect graph, 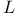 299 299
Perfect graph, h- 299
Perfect graph, t- 272Ч276 273
Perfect matching 17 203 203Ч208 230Ч233 255Ч259
Perfect matching polytope 205
Perfectly orderable graph 281
Permutation graph 280
Perron, O. 134 343
Picard, E. 338
Piecewise linear function 188
Pivot element 36
Pivoting 36Ч45
Pivoting rule 42
Planar graph 18
Plummer, M.D. 230 342
Pnueli, A. 280 335
Pointed polyhedron 9
polar 11 131 188
Polar cone 11
Polar,  - 180 - 180
Polyhedrai cone 9
Polyhedral function 188
Polyhedron 9 9Ч11
Polymatroid 304Ч324 306 316
Polymatroid intersection theorem 316
Polymatroid, extended 306 306Ч324 316
Polynomial approximation algorithm (scheme) 35
Polynomial computation algorithm with absolute (relative) error 34
Polynomial space algorithm 24
Polynomial time algorithm 24 27 54
Polynomial time algorithm, nondeterministic 24Ч26 25 56Ч63
Polynomial time algorithm, strongly 32 32Ч33 188Ч192 189 238
Polynomial time Turing reduction 28
Polynomial transformation 27
Polynomially computable from a given input with absolute (relative) error 34
Polytope 9
| Poorten, A. van der 35 343
Positive definite matrix 4
Positive semidefinite matrix 4
Potential 234 234Ч235 240
Power set 2
Predecessor 18
Prekopa, A. 345
Prim, R.C. 235 247 343
Primal program 15
Principal submatrix 2
Problem 21 21Ч22
Pulleyblank, W.R. 160 181 250 257 258 259 265 332 333 334 338 343 344
Q+-max-flow min-cut property 226 226Ч229
Q+-MFMC property 226 226Ч229
Quasi parity graph 283
Quintas, L.V. 332
R-arborescence 201 242
R-arborescence problem, shortest 201 201Ч203 242 242Ч243
r-cut 19
Rado, R. 304 344
Rank of a matrix 3 40
Rank of a matroid 211
Rao, M.R. vii 46 65 207 223 257 258 259 263 343
Ravindra, G. 282 343
Ray, extremal 184
Realization of an oracle 26
Recession cone 10 178
Recognition problem 279
Recski, A. 211 344
Reduced basis 141Ч146 142
Reduction, basis 139Ч156
Reinelt, G. vii 250 254 331 338
Relative error 34
Removal of a node set 17
Removal of an edge set 17
Riele, H.J.J. te 149 343
Rinaldi, G. 265 343
Ring family 313 313Ч319 325Ч329
Rinnooy Kan, A.H.G. 338 343
Rockafellar, R.T. 1 344
Rooij, A. van 280 344
Root of a digraph 19 201 242
Root of a matrix 4
Rooted arborescence 20 201 242
Rooted cut 19 201
Rooted cut packing problem 243
Rose, D.J. 281 344
Row sum norm 7
Roy, B. 331
Running time function 23 24
Rustin, R. 334
Sachs, H. 281 344
Sauer, N. 334 344
Saunders, M.A. 66 337
Sbihi, N. 282 302 344
Scheme, fully polynomial approximation 35
Scheme, polynomial approximation 35
Schmidt, W.M. 146 344
Schnorr, C.P. 146 344
Schoenberg, I.J. 35
Schoenheim, J. 334 344
Schrader, R. 65 344
Schrijver, A. 1 13 65 107 159 193 199 218 252 253 259 274 275 283 285 324 326 337 338 344
Separating cut 207
Separation from extended polymatroids 309
Separation oracle 55
Separation oracle of a lattice 151 151Ч154
Separation problem, shallow 94Ч101
Separation problem, strong 48 48Ч50 170Ч181
Separation problem, weak 51 51Ч53 55 57Ч58 62 102Ч122 128Ч132 170Ч174
Series-parallel graph 273
Serre, J.-P. 335
Seymour, P.D. 200 250 259 261 262 267 268 275 282 337 339 343 344 345
Shallow  -cut 98 -cut 98
Shallow  -separation oracle 98 -separation oracle 98
Shallow cut 72 95 96
Shallow separation oracle 95 101
Shallow separation problem 94Ч101
Shallow- -cut ellipsoid method 98 -cut ellipsoid method 98
Shallow-cut ellipsoid method 83 94Ч101 96
Shamir, A. 221
Shannon, C.E. 199 335
Sheehan, J. 335
Shisha, O. 340
Shmoys, D. 338 343
Shortest (di)path problem 234 234Ч236
Shortest arborescence problem 245
Shortest circuit problem 22
Shortest lattice vector problem 140 143
Shortest multicommodity path problem 267
Shortest odd cycle problem 235
Shortest r-arborescence problem 201 242
Shot, N.Z. v 56 65 94 345
Sieveking, M. 45 155 337
Simple graph 17
simplex 10
Simplex method 41Ч43 64Ч66
Simultaneous diophantine approximation problem 138 138Ч139 146Ч156 168Ч170
Singular matrix 3
SIZE 23 30
Sliding objective function technique 107
Smale, S. 42 345
Small linear form problem 139 147
SMEM 48
SNEMPT 47
Solution of a problem 21 21Ч22
Sonnevend, G. 66 345
SOPT 47
Space complexity function 24
Spanning arborescence 20
Spanning tree 20
Spanning tree packing problem 251
Specker, E. 337
Spectral norm 7
Spencer, T. 243 247 336
Split graph 281
Splitter 327
SSEP 48
Stability number 229 229Ч233 272Ч303
Stable set 18 229 229Ч233 272Ч303
Stable set polytope 272 272Ч303
Standard form of a linear program 41
Standard representation of a polyhedron 9
Star 18 209
State 23
Steiglitz, K. 236 239 343
Step parameter 82
Stoer, J. 1 345
Strang, G. 1
Strassen, V. 40 337 345
Strazicky, B. 345
Strong connector 252 252Ч253
Strong cut 252
Strong membership problem 48 48Ч50 170Ч174
Strong nonemptiness problem 47 47Ч48 75 172 173Ч178
Strong optimization problem 47 47Ч50 162 162Ч163 171Ч172 179Ч180 191Ч192
Strong perfect graph conjecture 279
Strong separation problem 48 48Ч50 170Ч181
Strong unconstrained convex function minimization problem 55
Strong validity problem 47 47Ч50 170Ч172
Strong violation problem 47 47Ч50 170Ч172 179Ч180
Strongly connected digraph 19
Strongly connected subdigraph 247 252Ч253
Strongly perfect graph 282
Strongly polynomial time algorithm 32 32Ч33 188Ч192 189 238
Strongly t-perfect graph 274 274Ч275
Submodular circulation 320
Submodular function 304 304Ч308
Submodular function minimization 310 310Ч311 315 316 325Ч329
Submodular on crossing pairs 315
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -
-  -cut
-cut