|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grotschel M., Lovasz L., Schrijver A. — Geometric Algorithms and Combinatorial Optimization |
|
|
 |
| Предметный указатель |
Submodular on intersecting pairs 315
Submultiplicative norm 7
Subordinate norm 7
Subset sum problem 218—221 219
Subtour elimination constraints 263
Successor 18
Succinct certificate 25
Sum of two sets 128 188
Supply-demand theorem 233 305
Support function 49
Suranyi, J. 280 338
SVAL 47
SVIOL 47
Symmetric difference 2
Symmetric matrix 4
System of (linear) equations 9
System of (linear) inequalities 9
Szegoe, G. 93 343
Szelezsfin, J. 345
Szemerbdi, E. 344
T-cut 207 207—208 257—262 259 263
T-cut packing problem 260
t-extremal 58
t-hull of F 58
T-join 259 259—262
T-join packing problem 260
t-perfect graph 273 273—276
T-tape k-oracle Turing machine 26
tail 18
Tape 22
Tarasov, S.P. 181 340
Tardos, E. vi vii 158 168 169 189 190 198 238 335 345
Tarjan, R.E. 237 242 243 246 247 274 281 332 337 339 344 345
TDI 16
Terminal endnode 18
Terminus 19
Thatcher, J.W. 340
Thomassen, C. 236 345
Time complexity function 23 23—24 27
Tismenetsky, M. 1
Todd, M.J. 65 71 72 82 94 107 248 332
Tomlin, J.A. 66 337
Tooth 264
Total value of a multicommodity flow 266
Totally dual integral 16
Totally primal integral 16
Totally unimodular matrix 199 199—201 282—283
Tough ellipsoid 96
Tour 19
TPI 16
Trace 2
Trail 19
Transportation problem 232 232—233
Transposition 2
Traveling salesman problem 22 46 262 262—265
TREE 20 247—251 311—313
Tree, Gomory-Hu 249
triangle 19
Triangle inequality 5
Triangulated graph 280 302
Trotter, L.E., Jr. 45 281 301 302 334 337 342 345
Truemper, K. vii 201 275 282 336 342 345
Tucker, A.W. 339
Turing machine 22 22—23 26
Turing reduction 28
Tutte — Berge theorem 255
Tutte's perfect matching theorem 204
Tutte, W.T 25 204 206 208 222 251 255 256 258 259 346
Tutte-set 206
Uhry, J.P. 250 274 281 332 335
Ullman, J.D. 21 331
Uncrossing technique 244
Underlying graph 18
| Unimodular graph 281 281—282
Union of convex sets 129 188
Unit ball 6
Unit vector 2
Up-monotone 11
Upper integer part 2
Valid inequality 9
Validity oracle 55
Validity problem, strong 47 47—50 170—172
Validity problem, weak 51 51—53 55 57—58 62—63 102—122 128—132 170—172
Vazirani, V.V. 255 342
Veinott, A.F. 334 336
Vertex 9
Vertex of a polyhedron 181 183 184 190—192
Vertex-complexity 163 163—165
Vial, J.P. 66 337
Violation oracle 55
Violation problem, strong 47 47—50 170—172 179—180
Violation problem, weak 50 51—53 55 57—58 61—62 102—122 128—132 170—172
Vizing, V.G. 209 346
Volume 8 126
Wakabayashi, Y. vii
Walk 19
Warshall, S. 235 346
Weak constrained convex function minimization problem 55
Weak membership problem 51 51—55 56—58 61—63 102—122 128—132 170—174
Weak membership problem  56 56
Weak membership problem 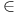 co- co- 57 57
Weak nonemptiness problem 51 51—53 171
Weak optimization problem 50 50—53 102—122 170—174 173
Weak separation problem 51 51—53 55 57—58 62 102—122 128—132 170—174
Weak separation problem  57 57
Weak validity problem 51 51—53 55 57—58 62—63 102—122 128—132 170—172
Weak validity problem  57 57
Weak validity problem 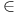 co- co- 57 57
Weak violation problem 50 51—53 55 57—58 61—62 102—122 128—132 170—172
Weak violation problem  57 57
Weakly triangulated graph 282
Weighted (perfect) b-matching problem 257
Weighted (perfect) matching problem 255 256
Well-bounded convex set 53
Well-characterized problem 25
Well-described lattice 151
Well-described polyhedron 163
Welsh, D.J.A. 211 346
Werra, D. de 281 333
Wheel constraint 300
Whitesides, S.H. 281 346
Whitman, D. 236 337
width 6 125
Will, H. 280 344
Wilson, R.J. 341
Witzgall, C. 1
WMEM 51
WNEMPT 51
Wolsey, L.A. 217 311 342 343
WOPT 50
Wright, M.H. 66 337
WSEP 51
WVAL 51
WVIOL 51
Yakovleva, M.A. 238 241 346
Yamnitski, B. 65 104 346
Yannakakis, M. 267 339
Yao, A.C. 247 346
Younger, D.H. 251 252 253 254 321 342
Yu, C.S. 302 331
Yudin, D.B. v 65 94 104 107 113 346
Z+-max-flow min-cut property 227 227—229 252
Z+-MFMC property 227 227—229 252
Zaw Win vii
Zuckerman, H.S. 134 342
[s, t]-cut 17 19
[s, t]-walk 19
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




 co-
co-