Авторизация
Поиск по указателям
Zeidler E. — Nonlinear Functional Analysis and Its Applications: Part 1: Fixed-Point Theorems
Обсудите книгу на научном форуме Нашли опечатку?
Название: Nonlinear Functional Analysis and Its Applications: Part 1: Fixed-Point TheoremsАвтор: Zeidler E. Аннотация: This is the first of a five-volume exposition of the main principles of nonlinear functional analysis and
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1986Количество страниц: 897Добавлена в каталог: 22.12.2011Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Retraction,trick for constructing fixed points 51 563 Riesz - Schauder theory for compact operators 372 Riesz - Schauder theory for dual pairs 788ff Rotation of a vector field 521 Saddle point of a dynamical system 93 Saddle point of a functional 457 Scalar product 785 Schauder fixed-point theorem 56 Schauder fixed-point theorem, generalized 500 556 624 725 Schauder fixed-point theorem, second 452 Schauder fixed-point theorem, with uniqueness 624 Selection 463 Selection theorem, finite sets (marriage theorem) 464 Selection theorem, topological spaces (Michael's selection theorem) 466 Semi-linear 804 Semi-linear differential equation see Applications to Semi-linear operator equations 60 398 Separable B-space 770 Separable topological space 751 Separation theorem for compact sets 636 Separation theorem for convex sets see Section 39.1 in Part III Separation theorem Jordan - Brouwer 580 Sequentially closed 759 Sequentially compact 759 Sequentially complete 762 Set 746 Set theory 745ff Set theory, basic theorems of 489 511 749 Set, absolutely convex 764 Set, absorbing 764 Set, algebraic 646 Set, analytic 646 Set, arcwise connected 758 Set, bounded 762 768 769 780 Set, Cantor 583 758 Set, circled 764 Set, closed 751 Set, compact 756 Set, connected 757 Set, convex 764 Set, dense 751 Set, directed 759 Set, finite 749 Set, infinite 749 Set, Julia 743 Set, locally arcwise connected 758 Set, massive see Residual Set, meager see of first Baire category Set, nowhere dense 751 Set, of first Baire category 802 Set, of normal structure 485 Set, of second Baire category 802 Set, open 751 Set, ordered 503 Set, perfect 754 Set, relatively closed 755 Set, relatively compact 756 Set, relatively open 755 Set, residual 802 Set, sequentially closed 759 760 Set, sequentially compact 759 760 Set, simply connected 758 Set, totally disconnected 757 Set, well-ordered 503 Sheaf theory 647; see Part V Shift operator 86 Shockwaves 113 simplex 599 Singular fixed point 184 Singular point 184 Singular value 184 Singular zero 184 Small divisor 103 220 223 smallest see Element Sobolev space 261; see Part II Space 800 Space, analytic 646ff Space, arcwise connected 758 Space, Banach (B-space) 769 Space, Banach manifold 180 Space, barrelled 783 Space, bornological 783 Space, compact 756 Space, connected 757 Space, contractible 609 Space, covering 727; see Part V Space, first countable 754 Space, fixed-point 609 Space, Fr 784 Space, function spaces see List of Symbols Space, Hausdorff see Separated Space, Hilbert (H-space) 785 Space, invariant 158 Space, Lebesgue 111 Space, Lindel 757 Space, linear 763 Space, linear topological see Topological space vector Space, locally arcwise connected 758 Space, locally compact 597 Space, locally connected 757 Space, locally convex 779 Space, manifold 181 Space, metric 761 Space, metrizable 762 Space, normal 596 Space, nuclear 784; see Part V Space, paracompact 597 Space, Polish 762 Space, regular 596 Space, second countable 754 Space, separable 751 Space, separated 754 Space, simply connected 758 Space, Sobolev 261 Space, topological 750 Space, topological vector 768 Space, totally disconnected 757 Spaces, schematic overviews of important 752 753 Spectral radius 795 Spectrum 795 Spectrum essential 497 Spectrum of compact operators 372 Splitting property 766 Stability of bifurcation solutions 386 424 Stability of biological equilibria 163 Stability of equilibrium points of dynamical systems 86 Stability of fixed points 158 160 Stability of fixed points of analytic maps 223 Stability of iterative methods 31 157 282 Stability of oscillations 91ff Stability of periodic solutions 162 200 202 Stability of planetary system 100 125 222 Stability of positive solutions 282 Stability of solutions of elliptic equations 323 324 Stability of solutions of parabolic equations 330 Stability, notions of bifurcation solution (asymptotically stable, weakly asymptotically stable, unstable) 424 Stability, notions of equilibrium point (asymptotically stable, stable, unstable) 86 Stability, notions of fixed point ( 160 Stability, notions of fixed point (asymptotically stable, stable, unstable) 158 Stability, notions of solution of an elliptic equation (asymptotically stable, weakly stable, unstable) 323 324 Stable homotopy 717 Stable manifold 93 112 Stable set 158 Stochastic particle reactions 124 Strange attractors 164 Strategy pair in game theory 461 462 Structural stability 95 99 100 106 Structure 800 Subimmersion 178 Subimmersion theorem 178 Submersion 183 Submersion Theorem 185 Support 756 Supremum in ordered sets 503 Suspension 715 Switching circuits 96 Symmetry in nature 109 Symplectic geometry 734; see Part V Synergetics 656 Tangent see Part IV Tangent bundle 183 Tangent space 183 Tangential map 183 192; Tangential map and the chain rule for higher derivatives 192 Taylor's theorem 148 Taylor's theorem, converse of 193 Theorem see also Fixed-point theorem Theorem, Alaoglu - Bourbaki 777 782 Theorem, approximation 55 533 770 Theorem, Arzel 772 Theorem, Atiyah - J 727; see Part V Theorem, Atiyah - Singer index 372 727; Theorem, B 434 Theorem, Baire - Hausdorff 776 802 Theorem, Banach 111 779 782 Theorem, Banach - Steinhaus 111 Theorem, beer barrel 846 Theorem, Bernstein 246 251 Theorem, Bing - Nagata - Smimov metrization 597 Theorem, bipolar see Part III Theorem, Birkhoff - Kellogg 559 Theorem, Borsuk - Ulam 708 Theorem, Borsuk antipodal 701 Theorem, Borsuk homotopy extension 698 Theorem, Bott periodicity 727 Theorem, bread-ham-cheese 710 Theorem, Brouwer - Schauder invariance of domain 705 Theorem, Brouwer fixed-point index 535 Theorem, Brouwer invariance of dimension 581 Theorem, Brouwer mapping classes 692 711 Theorem, bunch 392 Theorem, Caccioppoli 174 Theorem, closed graph 779 Theorem, closed graph, nonlinear 471 Theorem, closed range 111 Theorem, Cohen independence 748 749 Theorem, Crandall - Rabinowitz 383 426 Theorem, Cronin - Schwartz 621 Theorem, curve selection 639 647 Theorem, Dancer - Turner 669 Theorem, Eberlein- 111 Theorem, embedding 233 Theorem, Euler polyhedral 727; see Part V Theorem, extension see Extension of Theorem, for semi-linear equations 398 Theorem, Frobenius 167 343 Theorem, G 749 Theorem, Gauss - Bonnet - Chern 727; see Part V Theorem, general mean value 76 Theorem, generalized Frobenius 167 Theorem, generalized Gronwall 281 Theorem, generalized Peano 81 Theorem, generalized Picard - Lindelof 78 Theorem, generalized Taylor 148 Theorem, Grobman - Hartman 100 Theorem, Gronwall 82 Theorem, Grundmann 421ff 640 Theorem, Hadamard 174 Theorem, Hahn - Banach 776 Theorem, hard implicit function theorem (Moser - Nash) 218 Theorem, Hausdor ff Theorem, hedgehog see Poincare - Brouwer Theorem, Hess - Kato 347 Theorem, Hopf classification 711 Theorem, implicit function 150 Theorem, invariance of domain 705 Theorem, inverse mapping theorem, global 174 Theorem, inverse mapping theorem, local 172 Theorem, Ize 669 Theorem, Jentzsch 291 Theorem, Jordan - Brouwer separation 580 Theorem, Jordan curve 581 592 Theorem, Kantorovi 210 Theorem, Knaster- Kurato wski- M azurkiewicz 67 Theorem, Kneser - Fukuhara 567 Theorem, Krasnoselskii - Zabreiko - Steinlein mod 724 Theorem, Krasnoselskii cone expansion 562 Theorem, Krasnoselskii local bifurcation 666 Theorem, Krasnoselskii monotone minorant 286 Theorem, Krein - Milman see Section 38.7 in Part III) Theorem, Krein - Rutman 290 Theorem, Krein - Smuljan 782 Theorem, Leray - Schauder continuation 245 556 628 Theorem, Leray - Schauder fixed-point index 542 Theorem, Leray - Schauder unbounded component 631 Theorem, Leray- Schauder index 619 Theorem, Leray-product 575 Theorem, Ljapunov center 655; see Part IV Theorem, Ljapunov stability 87 99 Theorem, Ljusternik - Schnirelman - Borsuk 708 Theorem, Mackey - Arens see Part III Theorem, marriage 464 Theorem, Mazur 776 Theorem, Menger - N 594 Theorem, Michael selection 466 Theorem, Milman 475 Theorem, minimax 458 Theorem, Moser - Nash 218 Theorem, Moser twist 736 Theorem, Nagumo 122 Theorem, Nash embedding 220 Theorem, Nash equilibrium 469 Theorem, Noether 110; see Part V Theorem, nonlinear Krein - Rutman 312 Theorem, on generic finiteness 189 Theorem, on transflnite induction 511 Theorem, open mapping 111 Theorem, open mapping, nonlinear 705 Theorem, parametrized Sard 188 Theorem, Peano 57 Theorem, Perron 291 342 Theorem, Picard - Lindel 27 Theorem, Poincar 581 727; Theorem, Poincar 120 Theorem, Poincar 571 Theorem, Poincar 558 Theorem, Poincar 727; see Part V Theorem, preimage 185 Theorem, Rabinowitz global bifurcation 668 Theorem, rank 178 195 Theorem, Riemann - Roch 727; see Part V Theorem, Riesz compactness 111 Theorem, Riesz representation 785 Theorem, Sard 186 550 Theorem, Sard - Smale 186 550 Theorem, separation see Separation Theorem, Siegel center 223 Theorem, Smale complexity 257 Theorem, Spectral Mapping 798 Theorem, Sturm oscillation 792 Theorem, subimmersion 178 Theorem, Submersion 185 Theorem, Sundman 125 Theorem, surjective implicit function 177 Theorem, Taylor 148 Theorem, Tietze - Dugundji 49 65 756 Theorem, Tietze - Urysohn 756 Theorem, Tihonov product 756 Theorem, uniform boundedness 111 Theorem, Urysohn metrization 596
Реклама
 |
|
О проекте
|
|
О проекте



 chet (F-space)
chet (F-space)  f
f  -stable,
-stable, 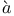 - Ascoli
- Ascoli  nich
nich  zout
zout 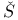 muljan
muljan 
