Авторизация
Поиск по указателям
Zeidler E. — Nonlinear Functional Analysis and Its Applications: Part 1: Fixed-Point Theorems
Обсудите книгу на научном форуме Нашли опечатку?
Название: Nonlinear Functional Analysis and Its Applications: Part 1: Fixed-Point TheoremsАвтор: Zeidler E. Аннотация: This is the first of a five-volume exposition of the main principles of nonlinear functional analysis and
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1986Количество страниц: 897Добавлена в каталог: 22.12.2011Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Fixed-point, trick for semi-linear equations 399 Formal languages 510 Formal languages, and the Tarski fixed-point theorem 511 Foundations of mathematics 746ff 806 Fourier series 787 Fr see F-derivative Fr 784 Fredholm alternatives, closed range theorem 111 Fredholm alternatives, compact operators 373 Fredholm alternatives, differential equations 259ff 792 Fredholm alternatives, dual pairs 788ff Fredholm alternatives, Fredholm operators 366 370 Fredholm alternatives, integral equations 788ff Fredholm integral equations of first kind 805 Fredholm integral equations of second kind 805 Fredholm mappings, linear 365 Fredholm mappings, nonlinear 366 Fredholm mappings, properties of 365ff Functional see Operator Functional calculus 798 (see also Part II) Functions of operators 797 Fundamental theorem of algebra and mapping degree 520 617 Fundamental theorem of algebra, generalized 639 Fundamental theorem of algebra, historical remarks 675 G see G-derivative G-derivative, basic definition 135 G-derivative, basic ideas 131 G-derivative, nth order 136 G-differential, basic definition 135 G-differential, basic ideas 131 Game theory 461 469 Gauge field theory 67 114 728; Generating order cone 276 Generic bifurcation 381 391 416 428 Generic finiteness of the solution set 189 Genericity 106 802 Genericity, as proof strategy 188 253ff 525 Gerschgorin disk 796 Graph norm 778 Graph of a map 448 748 GREATEST see Element Green's function 791 Green's function, and reduction of differential equations to integral equations 59 791 Green's function, generalized solution operator and 238 Green's function, positivity of 338 H 230ff H 232 H 248 H-isomorphism 785 Haar measure 67 466 Hard implicit function theorem 218ff Hausdorff dimension see Part V Hausdorff measure of noncompactness 611 Hausdorff metric 449 Hausdorff space 754 Hilbert space (H-space) 785 Hilbert space (H-space), important theorems in 787 Hilbert's problems 228 589 749 Historical remarks on Baire spaces 801 Historical remarks on Banach spaces 768 Historical remarks on bifurcation theory 350 395 Historical remarks on dimension theory 593ff Historical remarks on foundations of mathematics in the 19th century 582ff Historical remarks on Fredholm alternatives and Fredholm operators 370ff Historical remarks on functional analysis, linear 750 752 Historical remarks on functional analysis, nonlinear see Part V Historical remarks on fundamental theorem of algebra 675 Historical remarks on Hilbert spaces 784 Historical remarks on iterative solutions of differential and integral equations in the 19th century 15 Historical remarks on linear spaces 763 Historical remarks on locally convex spaces 779 Historical remarks on mapping degree 519 555 542 Historical remarks on metric spaces 761 Historical remarks on partial differential equations 226ff 236ff Historical remarks on positivity 269ff Historical remarks on set theory 589 745ff Historical remarks on topology 585 592ff 692 750 752 Homeomorphisms 755 Homeomorphisms, 755 Homeomorphisms, existence of global 174 649 705 706 Homeomorphisms, local 174 Homeomorphisms, local index of 577 Homeomorphisms, sign of 577 Homology 728; see Part V Homotopy invariance of essential maps 698 Homotopy invariance of fixed-point index 529 Homotopy invariance of mapping degree 570 Homotopy, basic definitions 527 Homotopy, classes 714 Homotopy, extension of a 698 Homotopy, groups 714 Homotopy, mod 569 Homotopy, stable 717 Homotopy, theory 714 Hopf bifurcation 411 438 655 663 Hull closed convex 764 Hull convex 764 Hull linear 764 Immersion 152 Implicit function theorem 150 Implicit function theorem, basic applications of the 151ff Implicit function theorem, basic ideas of the 150 Implicit function theorem, hard 218 Independence of axiom of choice 748 Independence of continuum hypothesis 749 Independence of parallel axiom 749 Index jump) proof strategies, fixed-point theory 10 61 188 253 Index of elliptic differential operators 259 Index of fixed points 529 532 Index of Fredholm operators 366 Index of integral operators and mapping degree 371 Index of linear operators 767 Index of zeros 524 533 Index theorem of Atiyah - Singer 372 727; Index theorem of Leray - Schauder 619 Induced topology (identical with subspace topology) 755 Inequality, abstract 281 Inequality, differential 887(see also Maximum principle) Inequality, Fan 449; see Part IV Inequality, Garding 794 Inequality, integral 82 281 Inequality, Poincar 794 Inequality, quasivariational 448; see Part IV Inequality, Variational 3 453 Infimum in an ordered set 503 Infinite-dimensional 765 Inner product see Scalar product Integrability condition 166 169ff 204 Integral equations, see Applications to Integral equations, and fixed-point theory 10 58 61 Integral equations, Fredholm 805 Integral equations, Hammerstein 805 Integral equations, Urysohn 805 Integral of vector functions of one real variable 75 Interior 751 Interior point 751 Intersection number 661 Interval mathematics 508 Interval mathematics, Newton's method in 513 Invariant manifold 112 412 Invariant set 112 158 Invariant subspaces of linear operators 66 Invariant tori 104 222 412 Inverse mappings, differentiation of 172 Inverse mappings, global theorem 174 Inverse mappings, local theorem 172 Isometry 761 Isomorphic B-spaces 771 Isomorphic H-spaces 785 Isomorphic linear spaces 764 Isomorphic manifolds 755 Isomorphic metric spaces 761 Isomorphic topological spaces 755 Isomorphic topological vector spaces 768 Iterative methods 16 21 481 Iterative methods for linear equations 30ff 35 40 343 Iterative methods for linear equations, block iteration 42 Iterative methods for linear equations, optimal relaxation 42 Iterative methods for linear equations, relaxation 41 Iterative methods for linear equations, single step 41 Iterative methods for linear equations, total step 41 Iterative methods, accelerated convergence 25 Iterative methods, basic ideas of 19 157 Iterative methods, for bifurcation problems 393 Iterative methods, for differential equations 28 240 324 327 330 Iterative methods, for eigenvalue problems 40 215 Iterative methods, for fixed-point problems 16 157 159 199 282 481 Iterative methods, for implicit functions 151 Iterative methods, for integral equations 28 58 Iterative methods, for regular semi-linear equations 398 Iterative methods, Newton's method and 206 Iterative methods, positivity and 282 343 Iterative methods, possible complex structure of 164 723 742 Iterative methods, rate of convergence see Rate Iterative methods, regularization and see Hard implicit function theorem Iterative methods, stable 31 Jets 804; see Part IV Jordan curve 119 592 Jordan curve theorem 119 581 592 Jordan normal form 373 Kolmogorov - Arnold - Moser theory (KAM-theory) 104 220 Kronecker elimination method 434 435 Kronecker existence principle 520 529 569 Kronecker integral and mapping degree 519 535 Lattice 503 Lattice, complete 504 Lebesgue integral see Part II Lebesgue measure see Part II Lebesgue space 771 Lemma see Theorem Leray - Schauder principle see Continuation method Limit cycle 98 119 408 Linear hull 764 Linear operator 764 Linear space 764 Linear subspace 764 Linearization may fail 5 359 409 736 Linearization principle 5 87 95 99 131 150 159 161 172 176 178 183 283 353 358 398 424 619 626 666 Linearization technique in differential calculus 131 Linearly independent 765 Linking number 727; see Part V Ljapunov - Schmidt method in bifurcation theory 375 Ljapunov center theorem 655; see Part IV Ljapunov function 84 Ljapunov stability 87 local 171 Locally convex space 779 Loop 758 Lower limit 761 Lower semi-continuous functional 456 760 Lower semi-continuous multivalued mapping 450 Lowerbound in an ordered set 503 M - S - Cauchy sequence in locally convex spaces 780 M - S - Cauchy sequence in uniform spaces 801 M - S-sequence 759 M - S-sequentially closed 759 M - S-sequentially compact 759 M - S-sequentially continuous 759 M - S-subsequence 760 Magnetic monopoles 111 729 Manifold see Banach manifold Manifold center, stable, and unstable 112; see Part V MAP see Operator Map, multivalued 447 Map, single-valued 748 Mapping degree see Fixed-point index Mapping degree for special classes of operators, 604 Mapping degree for special classes of operators, analytic Fredholm maps 648 Mapping degree for special classes of operators, analytic type 645 Mapping degree for special classes of operators, basic situation (compact perturbations of identity) 569 608 Mapping degree for special classes of operators, classical analytic functions 616 Mapping degree for special classes of operators, compact perturbations of homeomorphisms 578 Mapping degree for special classes of operators, condensing perturbations of identity 568 607 Mapping degree for special classes of operators, continuous operators in 535 569 Mapping degree for special classes of operators, operators which lower dimension 526 681 695 716 Mapping degree for special classes of operators, overview of generalizations in Parts II and V 600 Mapping degree for special classes of operators, real functions 521 535 Mapping degree, basic definition via fixed-point index 531 Mapping degree, basic ideas 519ff Mapping degree, basic properties 568ff 574ff Mapping degree, coincidence degree 580 Mapping degree, construction of the 521 551 Mapping degree, local 532 Mapping degree, uniqueness of the 570 Markov chain 343 Mathematical biology 162 733 Mathematical economics 255 469 Mathematical logic 749 Matrix, adjoint 796 Matrix, norm 796 Matrix, positive (Frobenius — Perron theory) 342 Matrix, transposed 796 Maximal see Element Maximal chain 511 Maximum norm 772 Maximum principle, basic ideas 274 Maximum principle, for elliptic equations 334ff Maximum principle, for ordinary differential equations 334ff Maximum principle, for parabolic equations 337 Method, approximation see Approximation Method, averaging 203 Method, continuation see Continuation method Method, for computing the fixed-point index see Fixed-point index Method, iterative see Iterative method Method, Kronecker elimination 434 435 Method, line 124 Method, majorant 210 214 363 395 Method, Newton (see Newton's method) method, nonlinear Fourier method 124 Method, of a priori estimates see a priori estimates Method, of discretization 124; see Part II Method, of Green's function 59 791 Method, of Ljapunov - Schmidt in bifurcation theory 376 Method, of Ljapunov function 84 Method, of Newton diagram in bifurcation theory 432 Method, of Poincar 86 Method, of projection see Part II Method, of projection in bifurcation theory 379 Method, of quasilinearization 217 Method, of regula falsi 218 Method, of retraction 50 51 563 Method, of shift operator 86 Method, of subsolutions and supersolutions 271 282 286 Method, overview of important methods in nonlinear functional analysis 2ff Method, Rothe 124 Method, shooting 216 Metric 761 Metric space 761 Metrization 596 762 Metrization theorem 596 597 Minimal surfaces 250 Moore-Smith sequence see M-S- sequence Multiplicity of a characteristic number 374 Multiplicity of a characteristic number, algebraic 374 Multiplicity of a fixed point 617 Multivalued map 447 Multivalued map, continuous 451 Multivalued map, lower semi-continuous 450 Multivalued map, upper semi-continuous 450 Nested interval principle 762 Nested interval principle, generalized 495 783
Реклама
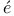chet derivative 
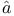teaux-derivative 
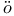lder continuous functions 
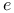-homeomorphisms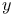 
-compact operators on closed convex sets 
|
|
О проекте