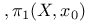|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Shafarevich I.R., Kostrikin A.I. (ed.) — Basic Notions of Algebra |
|
|
 |
| Предметный указатель |
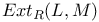 103 219—220 103 219—220
 -module (= Abelian group) 100 205 -module (= Abelian group) 100 205
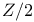 -grading 70 -grading 70
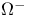 -hyperon 188 -hyperon 188
'Coordinatisation' 6—11 14 17 21 24—25 49 85 102 160 240
a.c.c. (= ascending chain condition) 41 44
Abel, N.H. 35 100 240
Abelian group 35 42 43 100 155 163 170 203 213
Abelian group, Lie algebra or ring 192
Absolute value (= modulus) of a quaternion |q| 65
Abstract group 100—102 104—108 151 240
Action of a group 104—105 132 192
Adele group 151
Adjoint action 105
Algebra 4—248 63 74
Algebra of differential forms 71
Algebra over a ring 63 203—204
Algebraic element of a field 48
Algebraic extension 48
Algebraic integers 61
Algebraic matrix group (= linear algebraic group) 150 155 157 159 181 224
Algebraic number field 31 61 103 235
Algebraically closed field 29 49 88 91
Algebraically dependent elements 47
Alternating group 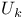 109 157 159 109 157 159
Alternative ring 200
Arithmetic genus 229
Arithmetic group or subgroup 132 133 150—151 224 239
Arnol'd, V.I. 143 242 243
Associative law 11 100 188 190 196 199 223
Atiyah — Singer index theorem 234
Atiyah, Sir Michael 234 239 240 241 242
Automorphic function 131 177
Automorphism 99
Automorphism of an extension 99 177—178
Axiomatic projective geometry 84 201
Banach, S. 38
Baobab tree 130
Baryons 185 187
Basis of free module 35
Bianchi, L. 172
Bieberbach, L. 126
Bogolyubov, N.N. 243
Boole, G, 22
Boolean ring 21—22 25 241
Borel, A. 240 243
Borel, E. 56
Bose, S.N. 162
Bosons 162
Boundary 213 215 217
Bouquet of topological spaces 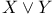 137 207 137 207
Bourbaki, N, 239 242 243
Braid group 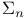 139 243 139 243
Brauer group Br K 93—96 103—104 237
Brauer, R.D. 95 103
Bravais lattices and groups 115—118 127
Bravais, A. 115
Brouwer fixed point theorem 215
Brouwer, L.E.J. 215
Brown, K.S. 241
Burnside's theorems 88—89 163 167
Burnside, W.S. 88 89 240
Campanula 130
Canonical homomorphism to quotient 28 36 107
Cartan, E. 197
Cartan, H. 241
Categories 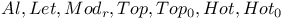 205 215 219 205 215 219
Category 202 204 225 241
Category of formal groups 206
Cauchy, A.L. 57 72
Cayley numbers (= octavions) 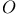 199—200 199—200
Cayley table (multiplication table) of a finite group 101 151
Cayley — Klein model of Lobachevsky space 105 131 132 149
Cayley, A. 101 105 200 241
Central algebra 90 103—104
Centre of an algebra 63 90
Chain conditions 41 44 77—78
Chain, complex 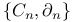 213 213
Chandler, B. 240 243
CHARACTER 89 163—165 167 173
Character of SU(2) 172—174 186
Character, group G 163—164 170
Characteristic of a field 31
Che valley, C. 91 240 243
Chevalley's theorem (finite fields are quasi-algebraically closed) 91
Class field theory 95
Class group: see ideal class group
Class number 36
Classical groups 144—150 157—158 174—176
Clebsch — Gordan formula (for representations of SU(2)) 173 186
Clebsch, R.F.A. 173
Clifford algebra C(L) 70 71 72 73 87 145 149 242
Clifford, W.K. 71 242
Coboundary homomorphism 213
Cochain complex 213
Cohomology 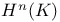 , , 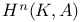 , , 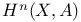 208 213 214 216 208 213 214 216
Cohomology ring 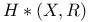 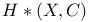 217 234 see sheaf long 217 234 see sheaf long
Commutative diagram 202
Commutative group: see Abelian group
Commutative Lie ring 192
Commutative ring 17—23
Commutative ring of continuous function 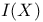 20 24 234—235 20 24 234—235
Commutative ring of differential operators ![$\mathbb{R}[\frak{\partial}{\partial x_1}, \cdots, \frak{\partial}{\partial x_n}]$](/math_tex/f7e1743e35452eb814d3f02c20c8d79082.gif) , , ![$\mathbb{C}[\frak{\partial}{\partial x_1}, \cdots, \frak{\partial}{\partial x_n}]$](/math_tex/a079df29bca678b431b14ebd99cb827182.gif) 19 33 34 42 71 189 19 33 34 42 71 189
Commutative ring of finite type 45
Commutative ring of germs of  functions functions 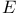 27 44 52 56 27 44 52 56
Commutative ring of germs of holomorphic functions 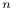 21 22 26 21 22 26
Commutative ring of integers 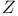 17 22 26 28 31 54 56 17 22 26 28 31 54 56
Commutative ring of integers of an algebraic number field 31 61 103 235
Commutative ring of p-adic integers 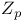 56—57 56—57
Commutative ring of polynomial functions on a curve K[C] 21 33 40 45 56 see polynomial
Commutator in a group G' 155—156 158—159
Commutator of differential operators (derivations) 189
Commutator [ , ] 189 194
Commuting differential operators 33
Compact Lie groups 143—147 167—174
Complement of a normal subgroup 223
Completion 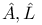 55—57 59 55—57 59
COMPLEX 214
Complex Lie groups 147—150 174—177
Complex manifold 47 147 148 226 228 229
Complex torus 48 143
Complexification of vector space 38
Composite of loops 136 210 211
Composition series 77—78 154
Congruence mod I 28
Conjugacy classes 106 109 165
Conjugate element or subgroup 106 109
Conjugate quaternion q 65 93 199
Conservation of momentum 98
Continuous geometry 87 242
Contragredient (= dual) representation p 165 166 172 188
Contravariant see functor tensor
Convolution 64
Coordinate ring K[C] 21 33 40 45 56
Coset (= residue class) mod I 28 36
Coset (left- or right-) 105—106
Covariant: see functor tensor
Crystal (or crystallographic) class 115 116 117 124 242
Crystallographic group 97—98 126—131 155
Crystallographic group in Lobachevsky plane 130—131
cube 110—111 158
Curvature tensor 172
CYCLE 215
Cycle type of a permutation 109
Cyclic group or subgroup 107 108 110 111 180
Cyclic module 43
de Fermat, P. 23
de Rham cohomology 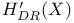 216—217 216—217
de Rham's theorem 217
de Rham, G-W. 216 217 241
| Dedekind, J.R.W. 239 241
Defining relations see generators and relations
Degenerate kernel 38
Degree of an extension [L : K] 48 99 182—183
Delone, B.N. 242
Demushkin, S.P. 183 243
Derivation 53 189
Derived functor see long exact cohomology sequence
Desargues' theorem or axiom 85—86 91 201 242
Desargues, G. 85 242
Descartes, R. 6
Deuring, M.F. 239 242
Diagram 202
Dictionary of quantum mechanics 8 38 185 186
Differential automorphism 181
Differential form 34 35 36 53 216 226
Differential Galois group 181
Differential of a complex 213
Differential operator 19
Differential operator on a manifold 53 193
Differential operator on a vector bundle 233
Dihedral group 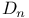 110 111 112 118 123 152 110 111 112 118 123 152
DIMENSION 41 206
Dimension of a Lie algebra dim if 191
Dimension of a variety dim C 47
Dirac equation 71 242
Dirac, P.A.M. 71 162 242
Direct product of groups 108 153 170 207
Direct sum of fields 83 163
Direct sum of modules 34 79 207
Direct sum of representations 76 88 89 162
Direct sum of rings 20 81 207
Dirichlet character 165
Dirichlet, P.G.L. 165
Discrete (= discontinuous) group 124—125
Discrete group in Lobachevsky space 131—133 243
Discrete series 177
Discrete subgroup of  125—128 125—128
Discrete transformation group 125 138
Divisibility theory in a ring 22 23
Division algebra 66 72 77 78 83—86 88 90—96 200 237
Division algebra over  91 201 233 239 91 201 233 239
Divisor on a Riemann surface 226 229
dodecahedron 110—111 158
Dold,A.E. 241
Dual category 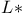 206 206
Dual module M* 39
Dual polyhedron 110—111
Dyson, F.J. 243
E.Noether's theorem (on symmetries and conservation laws) 98
Egyptian craftsmen 128 242—243
Eilenberg, S. 241
Einstein, A. 162
Elementary particles 158 162 174 185—188
Elliptic functions 126
Elliptic operator 233
Empty set 84
Endomorphism ring End^M 62 63 67 69 75 79 166
Engel, F. 240
Equivalent extensions 103
Equivalent functors 209
Equivalent lattices 115
Equivalent representations 76
Error-correcting code 30
Euclid (Euklides) 22 35 158
Euclidean algorithm 22 43 237
Euler characteristic 224
Euler characteristic of a group 224
Euler characteristic of a sheaf 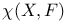 228—230 234 228—230 234
Euler equations for rigid body motion 198
Euler substitutions 16
Euler, L. 16 23 65 93 141 198 224 238
Evaluation homomorphism 24 27 51
Even Clifford algebra 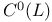 71 72 73 145 149 71 72 73 145 149
Even permutation 109 112
Exact sequence 218 226—228 231 236
Exceptional simple Lie groups 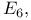 E_7 E_7 E_8 E_8 G_2 G_2 F_4$ 158 197 201 F_4$ 158 197 201
Extension of finite type 46
Extension of groups 154—155 223—224
Extension of modules 103 219—220
Extension of the group field 92 198
Exterior algebra of a module or vector space 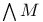 70—71 70—71
Exterior power of a module 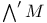 39 39
Exterior product 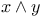 39 39
Factor group see quotient group
Factorisation 22 23 26—27 61
Family of vector space 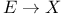 40 230 40 230
Fano's axiom in projective geometry 86
Fano, G. 86
Fedorov, E.S. 242
Fermi, E. 162
fermions 162
Feynman, R.P. 242
Field 11—17 26 29 72 235
Field of (formal) Laurent series K((t)) 16—17 21 56
Field of fractions of a ring 19 31
Field of meromorphic functions Ji(X) 16 47
Field of rational functions K(x), 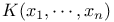 13 19 47 49 58 180 13 19 47 49 58 180
Field of trigonometric functions 16
Field, 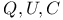 12 29 31 46 59 94 12 29 31 46 59 94
Field, extension L/K 12 29 46 49
Final object in a category 210
Finite abelian group 42 43
Finite dimension 41—45 191
Finite extension L/K 48—49 63 103 177
Finite field 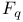 10 12 29 30 46 48 86 91 124 159 177 238 242 10 12 29 30 46 48 86 91 124 159 177 238 242
Finite geometry 9 86 91
Finite group 64 100—101 106 107 108—124
Finite group of algebraic type 159
Finite group of fractional-linear transformations 114
Finite group of orthogonal transformations 110 112—114 115
Finite length 77—78 153—154
Finite rank 41 63
Finite reflection groups 119 122—124
Finite sheeted cover 182—183
Finite simple groups 159
Finitely generated abelian group 44 153
Finitely generated algebra or ring over A (= of finite type) 45
Finitely generated extension 46—49
Finitely generated group 135
Finitely generated module (= of finite type) 42
Finitely presented group 135—136
First order linear differential operators 53 55 62 189
Flabby (= flasque) sheaf 227—228
Flabby resolution of a sheaf 228
Flag 110 168—169
Formal group (law) 197 206
Formal power series ring K[t], ![$K[x_1, \cdots, x_n]$](/math_tex/1fa81a1c5c8fc85a1983c42f2788c84982.gif) 21 56 21 56
Fourier coefficients 164
Fourier series 25 143 170 177
Fourier transform as isomorphism of modules 35
Fourier, J-B-J. 25 35 170
Fredholm operators 69 234
Fredholm, E.I. 69
Free action of a group 125 138
Free generators (= basis) 35
Free groups 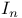 134 135 137 138 203 134 135 137 138 203
Free module 34—35 41 221
Free product of groups 203 207
Freudenthal, H. 241
Frobenius' theorem (on division algebras over  ) 91 ) 91
Frobenius, F. 91 240
Function field K(Q 14 31 47 49 91
Functional view of a ring 18 24 31 40 53—54 61 234—235 238 241
functor 207 208 215 219 226 231
Functor 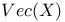 230 230
Fundamental domain for a discrete group 116 125
Fundamental group 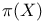 , \pi_1(X) , \pi_1(X)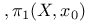 136—138 142 182 208 136—138 142 182 208
Fundamental Theorem of Galois Theory 179—182
Fundamental theorem of invariant theory 184
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



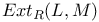
 -module (= Abelian group)
-module (= Abelian group)  -grading
-grading 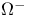 -hyperon
-hyperon 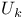
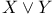
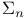
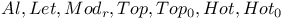
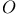
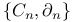
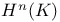 ,
, 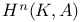 ,
, 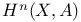
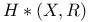
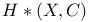
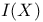
![$\mathbb{R}[\frak{\partial}{\partial x_1}, \cdots, \frak{\partial}{\partial x_n}]$](/math_tex/f7e1743e35452eb814d3f02c20c8d79082.gif) ,
, ![$\mathbb{C}[\frak{\partial}{\partial x_1}, \cdots, \frak{\partial}{\partial x_n}]$](/math_tex/a079df29bca678b431b14ebd99cb827182.gif)
 functions
functions 
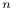
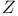
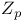
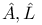
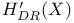
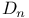


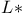
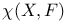
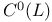
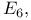 E_7
E_7 E_8
E_8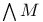
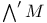
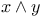
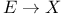
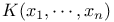
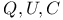
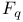
![$K[x_1, \cdots, x_n]$](/math_tex/1fa81a1c5c8fc85a1983c42f2788c84982.gif)
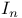
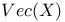
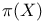 , \pi_1(X)
, \pi_1(X)