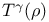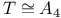|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Shafarevich I.R., Kostrikin A.I. (ed.) — Basic Notions of Algebra |
|
|
 |
| Предметный указатель |
Quotient ring (= residue class ring) 28
Quotient sheaf 226
Radical extension ![$K(\sqrt[n]{a})$](/math_tex/8b6167006bf36d7298a90c3c90cada0182.gif) 180 180
Rank of a module rank M 34 41
Rank of an algebra over a field 63 92
Rational fraction 12
Rational function 12
Rational function field K(x), 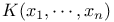 13 13
Rational function field of a curve or variety K(C) 14
Real part of a quaternion Re(q) 65
Reduced suspension SX 210—211 231 232
Reflection 97 98 119
Regular action (left-, right-) 105 193
Regular polyhedron 110—114 158 169
Regular representation 77 78 170 176—177 209
Remak, R. 153
Representable functors 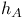 , , 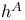 208—209 208—209
Representation of  and octahedral group 167 and octahedral group 167
Representation of a group 75—76 160—177
Representation of Abelian groups 163—165 170 173
Representation of an algebra 75
Representation of classical complex Lie groups 174—177
Representation of compact Lie groups 167—174 185—188
Representation of finite groups 119 163 240
Representation of semisimple ring 81—83 88—89
Representation of SO(3) 174
Representation of SO(4) 171—172
Representation of SU(2) 172—174 185—187
Residue class mod I 28
Ricci (trace-free) tensor 172
Ricci, C.G. 172
Riemann surface 31 58 126 131 137—138 226 229 241
Riemann — Roch theorem 229—230 234 241
Riemann, G.F.B. 31 58 72 169 172 224 230
Right coset, right ideal, right invariant, right regular see coset ideal invariant regular
Rigid body motions 140 195 198
Ring 17 62
Ring axioms 62
Ring of bounded operators on Banach space 62 69 87
Ring of differential operators 63 69 73
Ring of linear transformations: see endomorphism ring matrix coordinate- semisimple-)
Roch, G. 230
Rotation 110 112 140—142
Row and column operations 43 237
Ruler-and-compass construction 50
Salt NaCl 98
Schoenflies, A.M. 242
Schur's lemma 77
Schur, I. 77
Section of a family of vector spaces 40
Seifert, H. 241 243
Semidirect product of groups 223
Semigroup with unit 206 230
Semisimple module or ring 79 81 90 103 166 167 169 175 184
Serre, J.-P. 240
Set with operations 4 11 17 100
Sheaf 225—230
Sheaf associated with a divisor on a Riemann surface 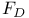 226 229 226 229
Sheaf cohomology 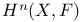 225—230 225—230
Shmidt, O.Yu. 153
Short exact sequence 218
Similar lattices 132
Simple algebraic groups 157
Simple central algebra 92 103—104
Simple compact Lie groups 157
Simple complex Lie groups 157 177
Simple finite groups 159
Simple group 154 155 158
Simple Lie algebra 192 197
Simple Lie groups 157 197
Simple module or ring 72 73 77 81 82 84
simplex 214
Simply connected 137 142
Singer, I.M. 234
Singular point of a variety 54
Skew field: see division algebra
Skew-isomorphic (= opposite) ring 67
Skew-isomorphism of rings 67 71
Smash product 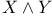 210 210
Solvable group 155—157 180
Solving a differential equation by quadratures 181—182
Solving an equation by radical 180
Soule, C. 243
Special linear group SL(n, k) 144 149 195
Special linear Lie algebra sl(n, K) 190—191 195
Speiser, A. 240
Spinor group Spin(n), Spin(p, q) 146 149
Sporadic simple groups 159
Stabiliser subgroup of a point 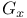 100 104 106 128 100 104 106 128
Stammbach, U. 241
Stapelia variegata 130
Stokes'theorem 216—217
Stokes, G.G. 216
Structure constants of an algebra 63 192 194
Subcomplex 217
| Subfield 12 30
Subgroup 104. See also Lie subgroup normal
Submanifold 32 200—201
Submodule 35
Submodule generated by a system of elements 36
Subrepresentation (= invariant subspace) 75 76 162 175
Subring 17 63
Subsheaf 225
Sum in a category 202 207
Sum of extensions of modules 103
Superalgebra (= 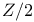 -graded algebra) 70 216 -graded algebra) 70 216
Suslin, A.A. 241 243
Suspension 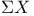 210—211 232 210—211 232
Switzer, R.M. 241
Symbol of an elliptic operator 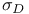 234 234
Symmetric group 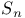 108—109 119 122 139 162 180—181 108—109 119 122 139 162 180—181
Symmetric power of a module S'M 39 184
Symmetric square of a module 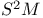 39 39
Symmetric—function 98 180
Symmetry 96—99 158 161 169 174 177 242
Symmetry breaking 174 185—187
Symmetry group of a crystal 97—98 126 242
Symmetry group of a lattice (Bravais group) 115—118 127
Symmetry group of a molecule 97 113
Symmetry group of a polynomial 98
Symmetry group of a regular polyhedron 111—112 158
Symmetry group of an ornament 97 128 242—243
Symmetry group of physical laws 98 99 242
Symmetry group of the n-cube 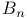 123 123
Symplectic group 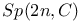 148 148
Tamagawa number 151
Tamagawa, T. 151
Tangent space 51—54
Taylor, B. 52 56
Tensor algebra of a vector space T(L) 67—68 183
Tensor of type 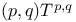 39 39
Tensor power 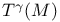 , , 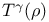 38 67 166 207—208 38 67 166 207—208
Tensor product of algebras or rings 92 104 166 204 207
Tensor product of modules 36—38 166 170 208
Tensor product of representations 166 167
Tensor, covariant or contravariant 38 39
Tetrahedral group 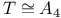 97 111—112 167 97 111—112 167
tetrahedron 97 110—112 158
The Monster 159
Threlfall, W. 241 243
Topology, topological space 102 125 136—140 213 225
Torsion element or module 42 43
Torus 143 243
Trace 88—89 90 173 195
Transcendence degree tr deg L/K 47
Transformation group 96 100 192 209 240
Transitive action or transformation group 100 106 143 169
Translation in a Lie group 142 195
Trivial family of vector spaces 230
Tsen's theorem (on division algebras over K(C)) 91
Tsen, C.T. 91
Twistor space 66
Two-sided ideal: see ideal
Ultraproduct of fields 32
Uniformisation of Riemann surfaces 126 131 137—138
Unique factorisation 22 61
Unique factorisation domain (UFD) 22 26
Unitary groups U(n), SU(n), SU(p,q), PSU(n) 144 158
Unitary Lie algebra u(n), su(n) 191 196
Unitary representation 169 177
Unitary symplectic group SpU(n) 145
Unitary symplectic Lie algebra spu(3n, K) 191
Unitary trick 175—176
Universal cover 138 142 182—183 197
Universal mapping property 37 202—204 207
Unramified cover of a space 125 142 182—183
Valuation of a field 57—61
Van der Waerden, B.L. 239 243
Vector bundle 230
Vector field 33 36 39 40 53 144 189 190 191 193 226 233
Vector space with a linear transformation 34 42 43 77 80 103
Vessiot, E. 181
von Helmholtz, H. 168 169 243
von Neumann, J. 242
Weber, H.F. 239 241
Wedderburn — Remak — Shmidt theorem 153
Wedderburn's theorem (on finite division algebras) 91
Wedderburn's theorem (on semisimple rings) 83 104
Wedderburn, J.H.M. 83 91 153
Weierstrass approximation theorem 170
Weierstrass preparation theorem 22
Weierstrass, K.T.W. 22 170
Weil, A. 239 241
Weyl tensor 172
Weyl, C.H.H. 6 172 193 240 242 243
Word 134
Word problem (= identity problem) for groups 135—136
Zeeman, P. 174
Zeta-function 238
Zhelobenko, D.P. 240 243
Zorn, M.A. 29
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



![$K(\sqrt[n]{a})$](/math_tex/8b6167006bf36d7298a90c3c90cada0182.gif)
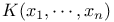
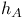 ,
, 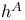
 and octahedral group
and octahedral group 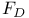
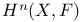
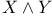
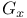
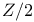 -graded algebra)
-graded algebra) 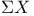
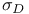
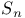
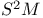
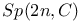
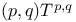
 ,
,