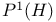|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Shafarevich I.R., Kostrikin A.I. (ed.) — Basic Notions of Algebra |
|
|
 |
| Предметный указатель |
Fundamental theorem of projective geometry 85
Galileo Galilei 6—7 99
Galileo — Newton group 99—100
Galois extension 99 178 225
Galois group 178
Galois theory 50 102 177 240
Galois, E. 90 102 177 179 239 240 242
Gauss' method (row and column operations) 43 237
Gauss, C.F. 23 43 94 239 240
Gaussian integers 23
General linear group GL(n, K), GL(K) 96 99 115 147 150 160 161 169—170 183 195 232
General linear group, Lie algebra 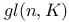 190 195 190 195
Generalised Cay ley algebra 201
Generalised quaternion algebra 93—95 237
Generators and relations 69 101—102 108 122—123 134—138 139
Generators of a group 101—102 104
Generators of a module 36 42
Generators of algebra or ring 45 68
Generic equation 181
Geometric construction of algebraic operations 13 50 85 242
Geranium 130
Germ of a function 27
Gordan, P.A. 173
Gorenstein, D. 240
Graded algebra or ring 46 63 68
Green, G. 217
Grothendieck, A. 241
Group 100 see knot Lie Lorentz orthogonal representation symmetry transformation unitary
Group 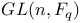 102 124 150 102 124 150
Group algebra or ring ![$\mathbb{Z}[G]$](/math_tex/010c3971fc8bdc636da66eeecd8afaec82.gif) , K [G] 64 75 163 222 237 , K [G] 64 75 163 222 237
Group character 162 167
Group cohomology 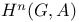 222—225 222—225
Group homomorphism 104
Group object in a category 209—210
Group of algebraic type 159
Group of an integral ternary quadratic form 132
Group of automorphisms of free module GL(n, A) 99 236
Group of extensions 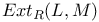 103 219—220 103 219—220
Group of finite length 153
Group of knot 138
Group of motions 96 97 107 156
Group of orders 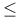 10—152 10—152
Group of rotations of 3-space SO(3) 112 140—142 195
Group, defined by relations 101—102 108 122—123 134—138 139
Group, generated by reflections 119 122—124 242
Hadamard, J.S. 242 243
Hamilton, W.R. 65 174
Hasse — Brauer — Noether theorem (on division algebras over  ) 95 ) 95
Hasse's theorem (on division algebra over  ) 95 ) 95
Hasse's theorem (on division algebra over 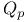 ) 93 ) 93
Hasse, H. 60 93 95
Haussdorff, F. 125
Heisenberg, W.K. 185
Helmholtz — Lie theorem 168—169 243
Hermite, C. 80
Hermitian scalar product 80 168
Higman's theorem 136
Higman, G. 136
Hilbert basis theorem 45
Hilbert, D. 8 45 80 184 239 242
Hilton, P.J. 241
Hirzebruch, F.E.P. 241 243
Hochschild, G.P. 240
Holder, O. 78 154
Hom( , A) and Hom(A, ) 208 209
Homeomorphism problem for manifolds 138
Homology 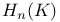 , , 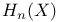 , , 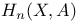 102 208 213—216 102 208 213—216
Homomorphic image (= quotient) 36 42 45 68
Homomorphism of families of vector spaces 40 230
Homomorphism of groups 104
Homomorphism of modules 36 74
Homomorphism of rings or algebras 24 28 31 63 192
Homomorphism of sheaves 225
Homomorphisms theorem 29 36 69 107
Homotopy theory 102 136 205 208—212 215 219 231—232 241
Hopf algebra 166
Huppert, B. 240
Hurwitz, A. 243
Ideal class group of a ring Cl A 36 61 102—103 235
Ideal of a commutative ring 26 28 32 36
Ideal of a Lie algebra 192
Ideal, generated by a system of elements 36 69
Ideal, left-, right-, two-sided- 68—69 73 83—84
Identity element 11 100
Identity morphism in a category 204
Identity problem (= word problem) for groups 135—136
Image of a homomorphism Im f 25 36 63 74 106 226
Imaginary part of a quaternion Im(q) 65
Incidence axioms 8—9 84
INDEX 249—258
Index of a subgroup (G: H) 106 109
Index of an elliptic operator Ind 2—234
Index theorem 234 243
Infinite group 64 124
Infinite-dimensional representation 80 176—177
Infinitesimal 50—51 55 192
Instantaneous angular velocity 195
Integral domain 19
Integral of a differential form 216
Integral of motion 98
Integral over a group I(f) 168
Invariant differential form 142 168 176
Invariant Hermitian scalar product 80 148 165 168
Invariant of a division ring (algebra) 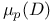 93—95 104 93—95 104
Invariant of a group 183 185
Invariant quadratic form 80 114 115
Invariant Riemannian metric 142 198
Invariant subspace 75 76 162 175
Invariant theory 160 183—184
Invariant vector field 142 193—194
Inverse 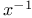 11 66 72 100 134 163 166 11 66 72 100 134 163 166
Inverse quaternion 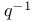 65 66 65 66
Invertible element 22
Involution of rings * 67 71 191
Irreducible polynomial 14 22
Irreducible representation (= simple module) 77 87 88 162 163 170 176
Isomorphism in a category 207
Isomorphism of fields and rings 13 17 24 29 63
Isomorphism of group actions 105
Isomorphism of groups 101
Isomorphism of ideals and modules 35 36
Isomorphism of Lie algebras 191
Isomorphism problem for groups 135—136 139
Isosahedral group 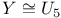 111—112 123 111—112 123
Isosahedron 110—112 158
Isotopic spin (isospin) 172—174 185—187
Jacobi identity 190
Jacobi, C.G.J. 190 191
Jets 55
Jordan normal form 43 80 103
Jordan — Hoelder theorem 78 154
Jordan's theorem on finite subgroups of 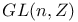 119 124 126 119 124 126
Jordan's theorem on finite subgroups of O(n) 118
Jordan, C. 43 78 80 118 119 154 239 240
K-theory 230—239
K-theory, 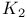 of a field of a field 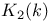 237 237
K-theory, 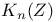 238—239 238—239
K-theory, K(A), 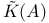 , , 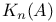 , , 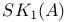 235—236 235—236
K-theory, K(X), 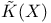 , , 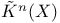 231 231
Kaplansky, I. 243
Kernel of homomorphism Ker f 26 63 68 106
Kernel of integral operator 38
Kernel of morphism of sheaves 226
Kirillov, A.A. 240
Klein, F. 105 239 240 241 243
Knot group 138—139
Koebe, P. 131
Kronecker, L. 239 241
Kurosh, A.G. 240
Lagrange's theorem (on sums of four squares) 66
| Lagrange, J.L. 23 66 98 240
Laplace, P.S. 72
Lattice 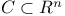 115 126 143 115 126 143
Laurent series 16 21 57 59
Laurent, P.A. 16 33
Left coset, left ideal, left invariant, left regular see coset ideal invariant regular
Legendre's theorem (on rational solutions of 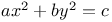 ) 60 94 132 ) 60 94 132
Legendre, A.M. 60
Length 77—78 79 153—154
Lie algebra of a Lie group 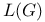 194—197 194—197
Lie algebra or ring 188—199
Lie group 125 140 142 143—150 192 210 240 see orthogonal unitary special spinor
Lie subgroup 143
Lie theory 192—199 206 240
Lie's theorem (on the Lie algebra of a Lie group) 196
Lie, M.S. 142 168 169 190 192 196 240 243
Linear dependent elements of a field 40
Linear differential operator 19 34
Linear differential operator of order 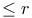 55 55
Linear map 36
Liouville's theorem (on integrable systems) 143 243
Liouville, J. 143 228 243
Lobachevsky plane 105 131 149 169
Lobachevsky, N.I. 105 130 243
Local Lie group 196
Long exact cohomology sequence 218—219 220—222 227—228 231 236
Long exact cohomology sequence of a subspace 218—219
Loop (= closed path) 136 182 208
Loop space 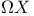 208 210 208 210
Lorentz group O(3,1), SO(3,1) 100 148—149 176
Lorentz, H.A. 100
MacDonald, I.G. 239 242
MacLane, S. 241
Magnus, W. 240 243
Mal'tsev, A.I. 242
Manifold 40 47 52 55 56 125 131 142 148 182 189 192 201 214 216—217 225 228 229 233
Manin, Yu.I. 70 240 241 242
Matrix algebra or ring 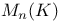 , , 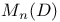 63 73 78 83 89 190 63 73 78 83 89 190
Maximal compact subgroup 148 158 224
Maximal ideal 29 32 40 51—52
Merkur'ev, A.S. 243
Meromorphic functions 16 47 181 226 229
Mesons 185
Milnor, J.W. 241
Minimal polynomial 48
Minkowski — Hasse theorem (on rational solutions of quadratic equations) 60
Minkowski, H. 60
Modular group 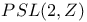 132—133 132—133
Module 33—34 74—79
Module of differential forms 34 35
Module of finite type (= finitely generated) 42 44
Module or rank zero 42
Module over  35 100 205 35 100 205
Module over a PID 43 235
Module over K[x] corresponding to linear transformation 34 42 43 77 80
Modulus (= absolute value) of a quaternion |q| 65
Momentum 98
Monodromy of a differential equation 115 162
Morphism in a category 204
Motions 96 195
Multiplication in modules 36
Multiplication table (= Cayley table) 101 151
Newton, Sir Isaac 99
Noether, A.E. 44 95 98 184 239 242
Noetherian module or ring 44—46
Nonassociative (division) algebra 199—200
Noncommutative ring 62
Noncommuting polynomial algebra 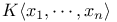 68 68
Nonsingular point of a variety 54
Nonstandard analysis 32
Normal subgroup 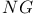 106 109 194 106 109 194
Normal subgroup of 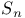 and and 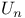 109 109
Normed field 57
Nucleon 185
Number of irreducible representations 88 163 165
Object of a category 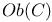 204 204
Octahedral group 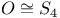 111—112 167 111—112 167
octahedron 110—111
Octavions (= Cayley numbers) O 199—200
Odd permutation 109
Opposite (= skew-isomorphic) ring 67 74 78 82
Orbit of an element Gx 100 106
Orbit space (= quotient) G\X 100 105 106 125 126 169
Order of a group element 107
Order of a group |G| 100
Orthogonal groups O(n), SO(n), PSO(n), O(p, q), SO(p,q), 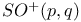 96 107 141 144 145 147 169 171 195 96 107 141 144 145 147 169 171 195
Orthogonal Lie algebras o(n,K), o(p,q) 190—191 195
Orthogonality of characters 164 167 169
Orwell, G.(Blair, E.A.) 31
Ostrowski's theorem (on valuations of Q) 59
Ostrowski, A. 59
p-adic field 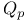 57 59 93 150 183 241 57 59 93 150 183 241
p-group 156
Pappus (Pappos of Alexandria) 85 91 242
Pappus' theorem or axiom 85 91 242
Parity law 100
Partially ordered set 84
Path or loop 136 208
Periodicity theorem in K-theory 232
Permutation group 98 102 108—109 119 179 240
Picard, C.E. 181
Plato (Platon) 110 158
Platonic solids 110—111 158 169
Poincare model of Lobachevsky space (upper half-plane) 105 131
Poincare — Koebe uniformisation theorem 131
Poincare, H. 105 131
Poisson bracket [,] 7 189
Poisson, S.D. 7 189
Polyhedron 110 112 117 214
Polynomial 18
Polynomial convex hull 25
Polynomial function on a curve 21
Polynomial ring A[x], ![$K[x_1,\cdots,x_n]$](/math_tex/285bd14ceca6a56a9512d44bb13b189182.gif) 17—19 26 45 55 56—57 17—19 26 45 55 56—57
Pontryagin duality theorem 171
Pontryagin, L.S. 171 240
Presheaf 225
Prime ideal 31 61
Prime subfield 30 48
Primitive Element Theorem 49
Principal ideal 26 27 36
Principal ideal domain (PID) 26 43 235
Product in a category 202 207
Product in cohomology 217
Product of differential forms 216
Product of fields 32
Product of ideals 27
Product of two modules with values in a third 36—37
Projective limit of rings 55
Projective module 221 235
Projective resolution of a module 221 232
Projective space 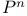 84 84
Projective space axioms 84
Projective space over a division algebra 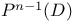 84 84
Puiseux expansion 59
Puiseux, V.A. 59
Purely imaginary quaternion 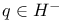 65 141 171 65 141 171
Quadratic reciprocity 94
quantum mechanics 8 172 174 185
Quark 188
Quasi-algebraically closed field 91
Quaternion 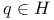 65 91 146 152 171 199 65 91 146 152 171 199
Quaternion of modules 1 SpU(l) 141 145
Quaternionic projective line 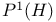 66 66
Quillen, D.G. 243
Quotient complex 217
Quotient group G/N 107
Quotient in a composition series 77 154
Quotient Lie algebra 192
Quotient module 36 42 75 76
Quotient representation 75 76
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



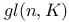
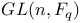
![$\mathbb{Z}[G]$](/math_tex/010c3971fc8bdc636da66eeecd8afaec82.gif) , K [G]
, K [G] 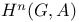
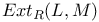
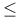
 )
) 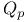 )
) 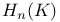 ,
, 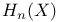 ,
, 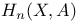
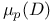
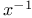
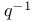
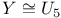
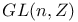
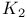 of a field
of a field 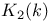
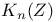
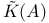 ,
, 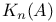 ,
, 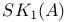
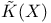 ,
, 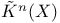
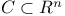
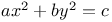 )
) 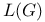
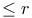
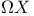
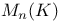 ,
, 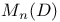
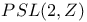

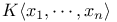
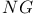
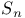 and
and 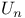
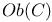
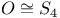
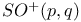
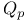
![$K[x_1,\cdots,x_n]$](/math_tex/285bd14ceca6a56a9512d44bb13b189182.gif)