|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rosenfeld B.A. (Author), Shenitzer A. (Translator), Grant H. (Assistant) Ч A history of non-Euclidean geometry: evolution of the concept of a geometric space |
|
|
 |
| ѕредметный указатель |
Poncelet, Jean Victor 148Ч149 228 402
Pont, Jean Claude 109n. 302
Pontryagin, Lev Semenovi 278 349Ч350 366 278 349Ч350 366
Posidonius 41Ч44
Positives (adfirmata) 163Ч164
Positivist philosophy 199Ч201 205
Power series 178 273
Pr nas 12 nas 12
Prad sa (atom of space) 195 sa (atom of space) 195
Principal character 407
Principal sections 280
Proclus 41Ч42 71 93 110Ч111
Progressions, geometric 160
Projections 116Ч121 127Ч128 134 140Ч142 147 149 341-342
Projective correspondence 121
Projective figure 149
Projective metrics 220 233 235Ч236 238
Projective ranges 121
Projective relations or properties 149
proportionality 225Ч226 318
Psellus, Michael 155Ч156 158Ч159
Pseudo vectors 167
Pseudo Ч T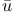 s s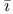 81 81
Pseudosphere 287 289
Ptolemy, Claudius 8Ч17 passim 24 43 117 123Ч124 175 300
Pythagoras 38 196
Pythagoreans 35 111 152 185Ч186 191 194
Quadrants 27Ч30 235 298
Quadratic forms 284 324 358
Quadratic irrationalities 35
Quadratures 352Ч353
Quadrics 148 152 239Ч250 256 282Ч283 296Ч299 341Ч344 390-391
Quadrics, cardinalities of 421Ч422
Quadrics, Hermitian 362
Quadrilaterals 10 17 33Ч34 43 59Ч68 77Ч83 91Ч100
Quadrilaterals, complete, theorem of 7 11 71 119 120 148
Quadrilaterals, Ibn al-Haytham Ч Lambert 59 91 100
Quadrilaterals, Khayy m Ч Saccheri 71 73 76 91 104 230 m Ч Saccheri 71 73 76 91 104 230
Qualities (linear, corporeal, surface) 161Ч162
Quantics 233
Quantifier, universal 172Ч173
quantum mechanics 276Ч278 418Ч419
Quantum physics 278 426
Quantum theory 318Ч319
Quaternary forms, theory of 342
Quaternions 179 250Ч251 358 385Ч386 388Ч389 395 409-412
Quaternions, biquaternions 298 395 398 403
Quaternions, duoquatemions 403
Qurb n n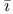 , Ab , Ab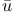 ТI Ч Q ТI Ч Q sim 56 sim 56
Qust ibn L ibn L q q 153 153
Ra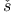 evski evski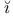 , Petr Konstantinovi , Petr Konstantinovi 366 366
RADIANS 31
Ranks 310
Rashed, Roshdi 155
Ratios 8Ч9 15 18 35 131 137 290- 291
Ratios, composite 20Ч21 97
Ratios, cross 118 121 136Ч137 148 236Ч246 296Ч297 362 406
Ratios, theory of 15 64 65 195
Rays 254Ч255
Rectangles 136Ч137 152
Rectangles, existence proved 54 57 59 68 83 87 91Ч99
Reflections 112 115 122 146 180 344Ч345 357
Reflections, along geodesics 317 364
Regiomontanus (Johann M ller) 22Ч24 ller) 22Ч24
Relationship 150
Relativity, general theory of 212 309Ч314 316 317
Relativity, Special Theory of 229 265Ч268 270 273 309 316 372
Rest, absolute 265
Reye, Theodor 174
Rham, Georges de 325
Rhomboid 37
Rhombus 37
Ricci Ч Curbastro, Gregorio 310Ч311 319
Richard of Middleton 183
Riemann topology 301Ч304
Riemann, Bernhard 173 203Ч204 257 266Ч267 276 321
Riemann, Cauchy Ч Riemann conditions 178 399
Riemann, Riemann symbols, four-inxed 294 411
Riemann, Riemann Ч Roch theorem 259Ч260
Riese, Adam 158
Riesz, Frigyes 274Ч275 308
Right-angle hypothesis 59 91 92 98
Rigid bodies 335Ч336 338
Ring theory 400Ч403 424
Roch, Gustav 259Ч260
Root extraction 154 170Ч171
Rosenfeld (RozenfelТd), Boris Abramovi 81n. 361n. 362 362n. 363 367 377 378 405 406 415Ч418 81n. 361n. 362 362n. 363 367 377 378 405 406 415Ч418
Rotation 126Ч127 258
Rudolff, Christoff 157 159Ч160
Ruffini, Paolo 154 327Ч328
Rule of four magnitudes 17Ч18
Rumyanceva, Lyudmila Viktorovna 362
Sabians (star worshippers) 15 24
Sabra, Abdelhamid Ibrahim 44 46 81 86n. 87n.
Saccheri, Girolamo 80 98Ч100 107 203
Saccheri, Khayyam Ч Saccheri quadrilaterals 71Ч73 76 83 94 104 230
Sagle, A. A. 412
Saint Venant, Ademar Jean Claude BarreТ de 177
Satake, Ichir , diagrams 359Ч360 369Ч371 422Ч423 425 , diagrams 359Ч360 369Ч371 422Ч423 425
Sayf al-Dawla 57
Scenography (perspective) 117 134
Sch nflies, Arthur 347 nflies, Arthur 347
Scheffers, Georg 399 403 404
Schellekens, Gerhard Johan 416
Schl fli, Ludwig 253 257 289 fli, Ludwig 253 257 289
Schlt ssel see Clavius Christopher ssel see Clavius Christopher
Schmidt, Otto Yulevi 333 333
Schoute, Peter Hendrik 256
Schouten, Jan Arnoldus 310Ч311 319 321
Schubert, Hermann 260
Schumacher, Heinrich Christian 215 220
Schur, Friedrich 295
Schutbert, Friedrich Theodor (Fedor Ivanovic 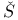 ubert) 147 ubert) 147
Schweikart, Ferdinand Carl 217Ч218 220
Sciences, Academy of 209Ч210
Sebokt, Severus 124
Secants, figure of 17Ч21
segments 174 252Ч253
Segre, Beniamino 422
Segre, Corrado 392Ч393
Seljuq dynasty 20
Semenova, Irina Nikolaevna 379Ч380
Semichord conjugate 115
Semicircles 5Ч6 8 110
Semiellipse 281
Series, convergent 104
Serre, Jean Pierre 425
Servois, Francois Joseph 138n.
Sets, topological 306Ч308
Severi, Francesco 260
Sexagesimals 10
Shadow 12 15
Shkolenok, Galina 142n.
Siddhantas 11Ч12 14
Silberstein, Ludwik 375Ч376 427
Simplices 308Ч309 345Ч346
Simplicius 42Ч46 68 69 85 86 89 105 190
Sindhind 11
SINEs 10Ч19 passim 23Ч26 31 214
Sitter, Willem de 313 314
Skew-symmetry condition 150
Skopec, Zalman Alterovi 415 415
Slavutin, Evgeni! Iosifovi 155n. 163n. 155n. 163n.
Smorodinskil, Yakov Abramovi 272 273 272 273
Snyder, Hartland 427
Socrates 186Ч187
Sohnke, Leonhard 346Ч347
Sokolov, A. A. 426 427
Solitons 380Ч381
Solstices 2 129
| Sommerfeld, Arnold 270 272
Sommerville, Duncan Maclaren Young 372 375 376
spaces 179Ч211 passim 228Ч245 247Ч279 290Ч325 334 351 359 372 375-377
Spaces, finite 424
Spaces, G-elliptic and G-hyperbolic 415
Spaces, Galilean 381
Spaces, Hermitian elliptic 406Ч407
Spaces, Hjelmslev 406
Spaces, imaginary 161
Spaces, MinkowskiТs space 418
Spaces, multidimensional 162
Spaces, parabolic 368
Spaces, reductive 368
Spaces, symmetric 363
Spacetime 277 309 311Ч313 317Ч318 418Ч419 426-427
Spampinato, Nicol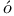 405 405
Spatial chain 228
Spatial complexes 302
Species 304
Spheres 3Ч4 27Ч33 229Ч235 280 302Ч303 321Ч326 344
Spheres,  -dimensional 256 -dimensional 256
Spheres, armillary 124
Spheres, as blocks 424
Spheres, EuclidТs definition 110
Spheres, Loba evskiiТs definition 211 evskiiТs definition 211
Spheres, real, pure imaginary, or null radii 229 302Ч303 321Ч326 344
Spheres, volume computed 219
Spherical astronomy 17
Spherical cosine theorem 12Ч15 19 22Ч25 29 170 223Ч224
Spherical Pythagoras theorem 13 223
Spherical sine theorem 11Ч20 22 223Ч224
Spherical tangent theorem 11 16Ч17 19Ч20 223
Spherical triangles 5Ч34 passim 39Ч40 83 101 206 222Ч226 295
Spherical trigonometry see Trigonometry
Spheroid 33
Spider see Arachne
Spinor representations 397 409Ч410 415 418
spirals 167 175 337
Spiritualists 204
Spivak, Michael 256
Stab (directed segments) 253
Staudt, Christian von 174
Steenrod, Norman 322
Steiner, Jacob 423Ч424
Steklov, Vladimir Andreevi 275Ч276 275Ч276
Stepa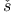 ko, Tamara Andreevna 417 ko, Tamara Andreevna 417
Stereographic projection 121Ч130 134 147 242 244 342Ч343
Stereography 134
Stereometric propositions 5 24
Stevin, Simon 175Ч176
StevinТs parallelogram 176
Stifel, Michael 159Ч161
Stipani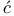 , Ernest 93 , Ernest 93
Stretch 251
Stringham, Washington Irving 256
Strubecker, Karl 376
Structure 398 416
Study, Eduard 299n. 361Ч366 395Ч398 409 420
Substitutions, real 239
Sude, Barbara Huper 59
Sufficient reason 185Ч186
Suida 124
Sums, partial 104
Sun 12 14 19Ч20
Sundials 15 123 167Ч168
Superposition 52 112 294 334Ч338
Surface-direction 293
Surfaces 111 160 201Ч204001 211 230Ч245 281Ч304 326
Sursolida 158Ч159
Symmetric forms 22
Symmetry 122 144 146 256 306 323 368Ч370
Tangency 156 197Ч198 246 270Ч271 280 281 286Ч287 322-323
Tangency, and cyclic points 149
Tangency, conics 116 135 235
Tangency, double 259
Tangency, ecliptic representation 126
Tangency, plane 242
Tangency, point of 122 140
Tangency, transformations mapping spheres onto spheres 344
Tapero, Tatyana Borisovna 279
Tartaglia, Niccolo 157
Taurinus, Franz Adolf 217Ч219 224
Taylor series 226
Tensors 310Ч311 321 323 325 364 366 420
Terminology, origins 11 22Ч23 156 158 159 168 187 302
Tetrads 120 148 420
Tetrahedra 195 256 345 347
Thales 110Ч111
Thas, Jacques 424
Theaetetus 35
Theodosius 3Ч5 110
Theon 123Ч124
Tihonov, Andrei Nikolaevi (Tychonoff) 309 (Tychonoff) 309
Time 19Ч20 199 201Ч202 205
Tits, Jacques 367 416 424Ч425
Tlla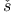 ev, Hamid Hasanovi ev, Hamid Hasanovi 81 81
Tlupova, Rimma Gumarovna 415Ч416
Toghr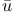 l, B l, B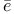 k 20 k 20
topology 203 212 257 268Ч269 301Ч309 322 325
Topology, combinatorial 173 260
Topology, groups 349Ч350
Torus 111 302 303 326
Totality 254Ч255 273 297 349
Toth, Imre 40n.
Touching 211
Toupin, R. A. 378
Tractrix 287
Trajectories, orthogonal 146 178 230
Transfmite 161
Transformations 136Ч138 142Ч151 264 274 320 338Ч344 413 415
Transformations, affine 130Ч133 320 323 393
Transformations, affine, affinities, axial 112Ч114 130 140
Transformations, affine, dilatations, central 112 115 30 40
Transformations, birationai 116 40Ч42 347Ч348
Transformations, circular 244
Transformations, conformal 323 361 418 420
Transformations, coordinate 278 310Ч311
Transformations, equiaffine 131
Transformations, fractional linear 237 239 346
transformations, geometric 134 348
Transformations, infinitesimai 351 353
Transformations, linear 297 348 354 388 407Ч408
Transformations, Lorentz 418
Transformations, projective 133Ч134 135Ч150 323
Transformations, symplectic 362 406
Triangles 22 50 78Ч91 100Ч111 163Ч168 206Ч208 214Ч228 286- 292
Triangles, angle sums 244
Triangles, equal 64
Triangles, homologous 140 417
Triangles, right 12 17Ч19 92 122 186
Triangles, spherical see Spherical triangles
Trigonometry 7 11Ч27 31 33 36 219Ч228 230
Triplets 179
Tympanums 123 126
Unguru, Sabetai 90
Unit disk 241
Unit segment 163
Unit sphere 249 415
Uryson, Pavel Samuilovi (Urysohn) 308 (Urysohn) 308
Utkramajya 12
VACUUM 182Ч183 185 194
Valences 310Ч311
Van der Waerden, Bartel Lendert 260 355
Van Roomen, Adrian 165Ч167
Van Schooten, Franz 159
Var hamihira 14 hamihira 14
Vari ak, Vladimir 272 ak, Vladimir 272
Variables 178 239 254 257 273Ч274 276 343
Veblen, Oswald 318 321 420
Vectors 167Ч179 passim 251Ч253 263Ч264 316Ч325 351Ч368 385 403 418 420
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте




 nas
nas  sa (atom of space)
sa (atom of space) 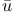 s
s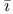
 q
q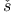 evski
evski , Petr Konstantinovi
, Petr Konstantinovi , diagrams
, diagrams  nflies, Arthur
nflies, Arthur  ubert)
ubert) 
 -dimensional
-dimensional  , Ernest
, Ernest  k
k