|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rosenfeld B.A. (Author), Shenitzer A. (Translator), Grant H. (Assistant) Ч A history of non-Euclidean geometry: evolution of the concept of a geometric space |
|
|
 |
| ѕредметный указатель |
Darboux, Gaston 343 361
Day-planes 127
De Lahire, Philippe 128n.
de Moivre formula 146
de Morgan, Augustus 382Ч383 398Ч399
Declinations 12Ч13 15
Dedekind, Richard 305 402Ч403
Deferents 175
Defrise, P. 378
Delian problem, classical 111
Dembowski, Peter 423
Democritus 182Ч183 190 194 196
Denisova, Natalya Serafimovna 411
Derivation, doctrine of 200
derivatives 197 281Ч284 292Ч294 310Ч311 316Ч317 351 364
Derivatives, partial 248 250 321
Desargues, Girard 136Ч140 416Ч417
Descartes, Ren 159 163 168Ч172 184Ч185 159 163 168Ч172 184Ч185
Determinants 250 255 342 352 389
Developability conditions 281
Dialectic method 198
Dickson, Leonard Eugene 411
Diderot 179Ч180
Differential equations 293 304 309 316 348 353
Differential equations, of geodesics 282 290
Differentials 197Ч198 270 282 302 317 324 334
Dilg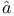 n, H n, H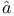 mit 86n. mit 86n.
Dimensionality, axiom of 263 279
Diodorus 42
Diophantus 153Ч155 167
Diopters 124
Dirac, Paul Adrian 278 418Ч419
Dirichlet, Peter Lejeune 380 401 402
Distance 211 229Ч238 241Ч244 255 258 264 272
Dodecahedra 256 345Ч346
Drum (tympanum astronomical instrument) 123Ч126 128Ч130
Du Val, Patrick 313Ч314
Duality principle 342 369Ч370
Dupin, Charles 281
Dynamics 141 202 265 266 268 312
Dynamis 152
Dynamodynamis 153
Dynamokybos 153
Dynkin, Eugene 355Ч357 360 369 371
DТAguillon, Francois 124 134
dТAlembert, Jean le Rond 177Ч180 185
Ecliptics 1Ч3 10Ч11 123 125Ч126 129-130
Egyptians 1
Ehresmann, Charles 325 366 425Ч426
Eigenvalues 258 273 278 354Ч355 390Ч391
Eigenvectors 354Ч355 367 390Ч391
Einstein, Albert 212 265Ч266 268 309 319
Electrodynamics 265
Ellipses 34 113Ч115 122 127 131Ч148 246 347
Ellipsoids 113 246
Encke, Johann Franz 219
Engel, Friedrich 348
Engels, Friedrich 189Ч190 204 257n.
Enriques, Federigo 260
Epicycles 175
Equator 3 128Ч129
Equator, celestial see Celestial equator
Equinoxes 2
Euclid 3Ч5 35Ч50 52Ч100 110 112 188 218 262 383 384
Euclid, axioms and four-dimensional rectangular coordinates 337
Euclid, definitions of square, cubic, plane, and solid numbers 152
Euclid, proportions Уby equalityФ 119
Euclid, stereometric propositions 24
Euclid, straight line indefinite extension 183
Euclid, three-dimensional analogues 156
Eudemus 110
Eudoxus 35 89Ч90 92 123 191
Eudoxus, Eudoxus Ч Archimedes axiom 39 44 47 51 54 57Ч59 262n.
Euler curves classified by 258Ч259
Euler geometry of position 173 301Ч302
Euler Latin squares 421
Euler motion of fluids 178
Euler stereographic projection of sphere onto plane 130
Euler theorem 255 304
Euler, Leonhard 31Ч34 102 143Ч150 185 275 280Ч283 388- 391
Eutocius 65
Exhaustion, method of 35 131Ч132 191
Extensions 210 252 351 424
Faces 255Ч256
Fano, Gino 420
Farpetzi, Ghazar 42
Fedenko, Anatoli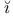 Semenovi Semenovi 364 364
Fedorov, Evgraf Stepanovi 347 347
Fermat, Pierre 162Ч163 168Ч170 401Ч402
Fibrations (fiber spaces) 321Ч323 418
Field quantization 278
Field theory, unified 317Ч320
Fields 395 400Ч402 404 408Ч409 420 425
Figures, concave and subconcave 162
Finikov, Sergei Pavlovi 323 323
Flag 260
foci 34 135Ч136 149 296
Fomin, Viktor Egorovi 279 279
Fourier, Jean Baptiste 274Ч275
Fractions, continued 95
Frames of reference 265 268
Francesca, Piero della 134
Frcchet, Maurice 304Ч306
Frenet, Frederic 324
Fresnel, Augustin J. 266
Freudenthal, Hans 387 416Ч418
Friedmann (Fridman), Aleksandr Aleksandrovi 313 313
Frisius, Gemma 129n.
Frobenius, Georg 403 404 407Ч408
Fubini, Guido Ghirin 361 363
Fuchs, Lazarus 239 241 346
Functions 1 142 219Ч232 271Ч278 289Ч292 305 346-347
Functions, abelian 259 302
Functions, analytic 147 150 178 399
Functions, curvilinear coordinates introduced by Gauss 283
Functions, exponential 31
Functions, HamiltonТs 380Ч381
Functions, homogeneous 248Ч250 334
Functions, linear 255
Functions, linear vector function 393
Functions, monodromy property 336
Functions, point 309 319Ч320
Functions, quadratic 250
Functions, wave 419
Fuss, Nicolai Ivanovi 33Ч34 33Ч34
Galen 300
Galilei, Galileo 375
Galois, Evariste 328Ч333 348 352 400Ч401 420 424
Gauss intrinsic geometry of a surface 291Ч292 294
Gauss quadratic forms 324
Gauss topological investigations 302
Gauss, Carl Friedrich 108 179 202Ч204 214Ч220 283Ч286 386 400-401
GelТfand, Izrail Moiseevi 366Ч367 377 366Ч367 377
Generators 93 299 342 410
Genus (of a curve) 259 302Ч303 347
Geodesy and geodesics 17 233 282Ч293 311Ч312 320 364
Geometric notions, origin of 200 202
Geometric theorems, auxiliary 22
geometries 1 34 85Ч101 152 180 204Ч246 279 289Ч302 420-427
Geometries, analytic 253Ч254 256
Geometries, atomistic 194
Geometries, elliptic 266
Geometries, enumerative 260
Geometries, existence doubted by Gauss 215
Geometries, Loba evskian 207 evskian 207
Geometries, multidimensional 251 254 256Ч258 260 276
Geometries, non Ч Euclidean 59 65 106Ч107 109 268 269 312Ч313 341
Geometries, plane 262 337 341Ч342
Geometries, projective 121 147Ч148 250 341- 343
Geometries, pseudo Ч Euclidean 266 309
| Geometries, quaternion symplectic 362
Geometries, Riemannian 316 359
Geometries, spherical 39 287
Geometries, symplectic 415
Geometries, synthetic projective 147Ч149 256
Geometry of position 173Ч174
Gergonne, Joseph Diaz 138n.
Gerling, Christian Ludwig 215 217 218
Gerson, Levi ben see Levi ben Gerson
Ghaznawl, Mahmud 16
Gibbs, Josiah Willard 393Ч394
Giordano, Vitale 96 173 211
Girard, Albert 27Ч31 34
Glagolev, Nil Aleksandrovi 378 378
Gleason, Andrew 350
Gluskov, Viktor Miha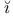 lovi lovi 350 350
Gnomon, vertical 12
Gois, Manuel de 161 183
Goldbach, Christian 385
Goldstein, Bernard R 90
Gondavo, Henry de 183
Gordon, Walter 381
Gosset, Thorold 346
Gottingen Scientific Society 220
Grassmann, Hermann G nther 174 251Ч261 289 301 393Ч399 408 nther 174 251Ч261 289 301 393Ч399 408
Graves, Charles 383Ч384 386Ч387 398-399
Graves, John Thomas 386Ч387 398
Gravitation 149 150 185 311Ч312 317
Gre , Nikolai Ivanovi , Nikolai Ivanovi 209 209
Greeks 1Ч2 10Ч11 181
Grigoryan, Edik, Sarkisovi 56 56
Grisogono, Federik Bartola i i 93 93
Grosseteste, Robert (Robert of Lincoln) 196
Grossmann, Marcel 309Ч310
groups 305 325 327Ч381 407Ч427
GurТev, Semen EmelТyanovi 104 107Ч108 104 107Ч108
H l l gu Kh gu Kh n 21 n 21
Half-chord (j va) 11 va) 11
Half-turn 112
Hamilton, William Rowan 166Ч167 179 250 380Ч382 385Ч387 393Ч394 398
Haritonova, Nade da Ivanovna 424 da Ivanovna 424
Harley, Henry 196
Harmonic mean 30
Harriot, Thomas 31
Hausdorff, Felix 306Ч308
Heaviside, Oliver 390 393Ч394
Hegel, Georg Wilhelm Friedrich 198 199
Heisenberg, Werner 318Ч319
Helgason, Sigurdur 364
Helmholtz, Hermann 267 333Ч338 348
hemisphere 123 128
Hermite, Charles 275
Hermitian forms 358 361Ч362 378Ч379
Heron 34 65 153
Hesse, Otto 341 362
hexagons 121
Hilbert, David 261Ч262 273Ч276 333 349Ч350 402 416Ч417 426
Hippocrates of Chios 35
Hjelmslev, Juhannes 406
Ho el, Jules 220Ч221 el, Jules 220Ч221
Homeomorphisms 255 306 331
Homogeneity principle 163 169
Homologies 140 143 304 308
Homomorphisms 403 407
Homotheties 112
Hoppe, Reinhold 256
Horizon 2Ч3 12 117 123 125 127
Horocycles 109 230Ч231 244 289
horoscopes 123
Horospheres 230Ч231 245
Hour angle 129Ч130
Hour lines 123 126n.
Hours 126Ч127
Hua, Loo Keng 405 415
Hudson, Hilda 347Ч348
Huygens, Christian 171Ч172 211Ч212 253
Hyperbolas 115 127 134Ч148 246 267Ч268 337 347
Hyperbolisms 142 347
Hyperboloids 93 113 229Ч230 245Ч246 266Ч267 297Ч298 344
Hypercones 376
Hypercycles 217
Hypergeometry 261
Hyperplanes 313 344Ч345 362 370 406Ч407 420
Hyperquadrics 376
Hyperspace 260Ч261
Hyperspheres 217 291 424
Hypersurfaces 291 313 324
Ibn al-Haytham, Abu СAl (Alhazen) 57 59Ч65 74Ч96 100 112 134Ч135 175 (Alhazen) 57 59Ч65 74Ч96 100 112 134Ч135 175
Ibn al-Nad m, Ab m, Ab l Ч Faraj Muhammad 40Ч41 l Ч Faraj Muhammad 40Ч41
Ibn Fath, Sin n 155 n 155
Ibn Qurra motion used in geometry 92 112
Ibn Qurra parallel postulate proof 77 83
Ibn Qurra rules for coordinate systemsТ transitions 167 168
Ibn Qurra, Th bit 15Ч16 20 23Ч24 41 49Ч60 96 131 bit 15Ч16 20 23Ч24 41 49Ч60 96 131
Ibn Rushd (Averroes) 183 196
Ibn S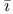 na, Ab na, Ab СAl СAl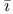 (Avicenna) 16 58Ч59 194 (Avicenna) 16 58Ч59 194
Ibn Sin n, Ibr n, Ibr h h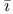 m 131Ч133 m 131Ч133
Ibn Y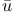 nis. Kam nis. Kam l al-D l al-D n 85 n 85
Ibn СIr q, Ab q, Ab Nasr Mans Nasr Mans r 5 16Ч20 r 5 16Ч20
Ichnography (plan) 117
Icosahedra 256 345Ч346
Ideae 117
Ideal 403Ч405
Idempotents 406
Identity axiom 306
Images 133 243Ч244
In n n , Erdal 377 , Erdal 377
Incendiary mirror (parabola) 135Ч136
Incidence axioms 262
Inclination of two planes, equal 3
India and Indian science 17
Indices (of a space) 264 279 313Ч314 361Ч362 399 409
Indivisibles 112 196Ч197
Inertia 312
infinity 39 98 102 143 161 181Ч183 296Ч297
Infinity, divisibility 85 190 192
Infinity, plane at 235
Infinity, points at 133Ч134 136 140 149Ч150 237
Infinity, simple 257
Initius Algebras 158
Integrals and integration 15 208Ч210 240 259 274 276Ч277 302
Integrals and integration, multiple 247Ч249 256 323
Invariance under rotation property 7
Invariants of algebraic forms 233 235 258 340
Inversions 114Ч116 118Ч119 142 242Ч245 340 347 415
Involutions 138Ч139 413
Involutive correlations 421Ч422
Involutory property 20Ч21
Isometries 146 320
Isomorphisms 333 346 351 361Ч363 403Ч410 420
Ivanenko, Dmitri Dmitrievi Dmitrievi 426Ч427 426Ч427
Jacobi, Carl Gustav Jacob 248Ч251 275 321 351 386
Jacobson, F. D. 413
Jacobson, Nathan 413
Jankiewicz, Czes aw (Yankevi aw (Yankevi ) 378 ) 378
Javadov, Maqsud Ali Simran oglu (D avadov) 405 410Ч411 415 avadov) 405 410Ч411 415
Jordan, Camille 257Ч258 324 333 338 346 348 392
Jordan, Paskual 412Ч415 417
Jung, F. 310 393
Kagan, Veniamin Fedorovi 80n. 80n.
Kallenberg, G. W. M 376
Kaluza, Theodor 318
Kant, Immanuel 179 187Ч188 203 208Ч210 215 218
Kantor, Isa LТvovi LТvovi 367 413 417 367 413 417
Kapralova, Sofya Borisovna 424
Karpova, Lyudmila Mihailovna 377 411
Kepler, Johann 31 134Ч136 196
Khayy m, Khayy m, Khayy m Ч Saccheri quadrilaterals 71Ч73 76 83 91Ч98 104 230 m Ч Saccheri quadrilaterals 71Ч73 76 83 91Ч98 104 230
Khayy m, theory of parallels 64Ч77 90Ч91 94Ч95 m, theory of parallels 64Ч77 90Ч91 94Ч95
Khayy m, СUmar 38 46 57Ч58 95 112 154 195 m, СUmar 38 46 57Ч58 95 112 154 195
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте




 n, H
n, H Semenovi
Semenovi
 nther
nther  i
i gu Kh
gu Kh va)
va)  da Ivanovna
da Ivanovna  el, Jules
el, Jules  n
n aw (Yankevi
aw (Yankevi