|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Morrison T.M. Ч Functional Analysis: An Introduction to Banach Space Theory |
|
|
 |
| ѕредметный указатель |
 32 32
 and block basic sequences 243Ч245 and block basic sequences 243Ч245
 and compact sets 189 and compact sets 189
 and matrix maps 96Ч98 and matrix maps 96Ч98
 and w.u.c.-series 283Ч284 285 and w.u.c.-series 283Ч284 285
 not complemented in not complemented in 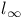 179 275 179 275
 not complemented in not complemented in 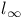 and projections 159Ч161 and projections 159Ч161
 not complemented in not complemented in 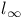 in Hilbert space or in Hilbert space or 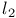 162Ч163 162Ч163
 not complemented in not complemented in 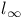 in spaces with basis 242Ч243 in spaces with basis 242Ч243
 not complemented in not complemented in 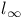 , finite-dimensional subspaces 161 , finite-dimensional subspaces 161
 , basis of 233 , basis of 233
 , basis of, has no boundedly complete basis 301 , basis of, has no boundedly complete basis 301
 , basis of, nonslirinking basis for 290 , basis of, nonslirinking basis for 290
 , basis of, shrinking 289 , basis of, shrinking 289
 , compact operators on 183 , compact operators on 183
 , complemented in separable spaces 163 , complemented in separable spaces 163
 , complemented subspaces isomorphic to , complemented subspaces isomorphic to  in 245Ч246 in 245Ч246
 , contained as subspace 283Ч285 , contained as subspace 283Ч285
 , dense subspace 42 , dense subspace 42
 , dual 44Ч45 , dual 44Ч45
 , Dunford Ч Pettis Property 306 , Dunford Ч Pettis Property 306
 , not a dual space 149 , not a dual space 149
 , not complemented in , not complemented in 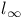 179 275 179 275
 , one operator ideal on 184 , one operator ideal on 184
 , separable 34 71 , separable 34 71
 , strictly singular operators on 202 , strictly singular operators on 202
 , unit ball not weakly compact 126Ч127 , unit ball not weakly compact 126Ч127
 , weakly compactly generated 176 , weakly compactly generated 176
 , when all operators into are weakly compact 177Ч179 , when all operators into are weakly compact 177Ч179
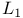 71 101 102Ч104 71 101 102Ч104
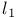 as dual of as dual of  44Ч45 44Ч45
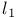 as dual of c 48Ч49 as dual of c 48Ч49
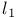 , boundedly complete basis 301 , boundedly complete basis 301
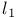 , coincidence of weak and norm sequential convergence in 276 , coincidence of weak and norm sequential convergence in 276
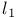 , compact and weakly compact operators into 182Ч183 , compact and weakly compact operators into 182Ч183
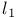 , complemented in bidual , complemented in bidual 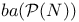 276 276
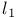 , contained in spaces with Schur property 259Ч260 , contained in spaces with Schur property 259Ч260
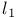 , dual 45 46 , dual 45 46
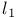 , has Dunford Ч Pettis Property 305Ч306 , has Dunford Ч Pettis Property 305Ч306
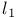 , is weakly sequentially complete 276Ч277 , is weakly sequentially complete 276Ч277
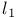 , Rosenthal's criteria for selecting basic sequence equivalent to , Rosenthal's criteria for selecting basic sequence equivalent to 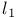 basis 259Ч267 basis 259Ч267
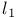 , separable spaces are quotients of, 103Ч104 , separable spaces are quotients of, 103Ч104
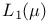 174 179 174 179
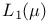 is weakly compactly generated 176 is weakly compactly generated 176
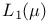 , continuity of linear maps into 103 , continuity of linear maps into 103
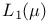 , dense subspace of 53 , dense subspace of 53
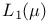 , dual of 54 , dual of 54
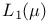 , has Dunford Ч Pettis Property 306 , has Dunford Ч Pettis Property 306
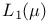 , has no boundedly complete basis 301 , has no boundedly complete basis 301
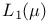 , not a dual space 149 , not a dual space 149
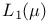 , unconditionally convergent series in 280Ч282 , unconditionally convergent series in 280Ч282
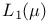 , when continuous operators on are weakly compact 181 , when continuous operators on are weakly compact 181
  29Ч32 36 104 see 29Ч32 36 104 see
  and compact sets 189 and compact sets 189
  , basis for 233 , basis for 233
  , basis for, block basic sequences in 243Ч246 , basis for, block basic sequences in 243Ч246
  , basis for, boundedly complete 301 , basis for, boundedly complete 301
  , basis for, shrinking 289Ч290 , basis for, shrinking 289Ч290
  , compact operators between 254Ч255 , compact operators between 254Ч255
  , dense subspace 42 , dense subspace 42
  , dual 46Ч48 , dual 46Ч48
  , isomorphic complemented subspaces in 245Ч246 , isomorphic complemented subspaces in 245Ч246
  , one operator ideal on 184 , one operator ideal on 184
  , separablility 33Ч34 , separablility 33Ч34
  , strictly singular operators on 202 , strictly singular operators on 202
  , total incomparability 255 256 , total incomparability 255 256
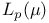  35Ч36 72 104 35Ч36 72 104
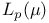  , compact sets in 189Ч190 , compact sets in 189Ч190
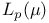  , dense subspace of 42 , dense subspace of 42
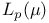  , dual of 54Ч56 , dual of 54Ч56
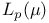  , Haar system for 234Ч237 , Haar system for 234Ч237
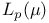  , Haar system for, is boundedly complete 301 , Haar system for, is boundedly complete 301
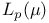  , Haar system for, is shrinking 290 , Haar system for, is shrinking 290
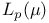  , is uniformly convex 336Ч337 , is uniformly convex 336Ч337
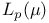  , is uniformly smooth 337 , is uniformly smooth 337
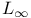 32Ч33 71 87Ч88 101 174 32Ч33 71 87Ч88 101 174
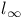 and Grothendieck spaces 175 and Grothendieck spaces 175
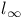 and matrix maps 96Ч98 and matrix maps 96Ч98
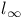 as dual of as dual of 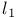 45Ч46 45Ч46
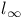 , ,  not complemented in 179 275 not complemented in 179 275
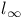 , dual 50 , dual 50
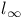 , lifting property of 82Ч83 , lifting property of 82Ч83
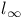 , noncompact operator on with compact square 196 , noncompact operator on with compact square 196
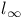 , nonseparability of 34 , nonseparability of 34
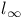 , representation of continuous linear operators on 274Ч275 , representation of continuous linear operators on 274Ч275
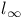 , separable subspaces not complemented 275 , separable subspaces not complemented 275
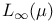 36 36
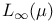 , dense subspace of 42 , dense subspace of 42
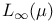 , has Dunford Ч Pettis property 306 , has Dunford Ч Pettis property 306
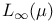 , pointwise limit of weakly compact operators in is weakly compact 179 , pointwise limit of weakly compact operators in is weakly compact 179
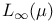 , weakly compact operators on 181 , weakly compact operators on 181
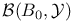 105 105
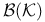 151Ч152 151Ч152
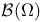 25Ч26 32 33 25Ч26 32 33
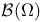 as as 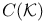 -space 26 -space 26
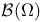 as dual of as dual of 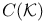 -space 59Ч60 -space 59Ч60
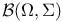 50Ч51 50Ч51
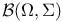 , dense subspace 50 , dense subspace 50
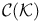 20Ч21 26 57 20Ч21 26 57
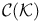 and separability 157Ч158 and separability 157Ч158
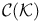 and Stone Ч Weierstrass Theorem 151Ч153 and Stone Ч Weierstrass Theorem 151Ч153
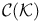 , dual 59Ч60 , dual 59Ч60
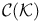 , extreme points in dual 148Ч149 , extreme points in dual 148Ч149
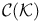 , has Dunford Ч Pettls Property 305 , has Dunford Ч Pettls Property 305
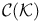 , weakly compact operators on 180Ч181 189 310 , weakly compact operators on 180Ч181 189 310
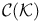 , weakly compact sets 189 , weakly compact sets 189
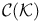 , when a Grothendieck space 175 , when a Grothendieck space 175
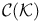 , when weakly sequentially complete 157 , when weakly sequentially complete 157
![$\mathcal{C}[0,1]$](/math_tex/5a7db169e0aa3351de258602580d65f182.gif) 19Ч20 26 82 104 19Ч20 26 82 104
![$\mathcal{C}[0,1]$](/math_tex/5a7db169e0aa3351de258602580d65f182.gif) and compact operators 185Ч186 189 and compact operators 185Ч186 189
![$\mathcal{C}[0,1]$](/math_tex/5a7db169e0aa3351de258602580d65f182.gif) , all separable spaces imbed in 142 , all separable spaces imbed in 142
![$\mathcal{C}[0,1]$](/math_tex/5a7db169e0aa3351de258602580d65f182.gif) , dense subspace, 42 , dense subspace, 42
![$\mathcal{C}[0,1]$](/math_tex/5a7db169e0aa3351de258602580d65f182.gif) , no boundedly complete basis 301 , no boundedly complete basis 301
![$\mathcal{C}[0,1]$](/math_tex/5a7db169e0aa3351de258602580d65f182.gif) , Schauder basis for 233Ч234 , Schauder basis for 233Ч234
![$\mathcal{C}[0,1]$](/math_tex/5a7db169e0aa3351de258602580d65f182.gif) , separable 33 , separable 33
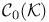 26Ч27 33 26Ч27 33
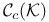 57Ч59 57Ч59
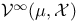 51-54 51-54
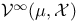 as dual of as dual of 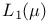 54 54
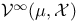 , realized as , realized as 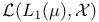 53 53
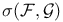 -topology 119Ч121 -topology 119Ч121
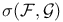 -topology, dual with respect to 119Ч120 -topology, dual with respect to 119Ч120
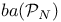 50Ч51 270 50Ч51 270
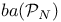 as dual of as dual of 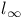 50Ч51 50Ч51
Absolutely summable series 27
Absorbing set(s) (radial at  ) 109 110Ч111 ) 109 110Ч111
Adjoint operator(s) 164 165Ч170
Adjoint operator(s) of strictly singular and cosingular operators 209Ч210
Adjoint operator(s), basic properties 166
Adjoint operator(s), closed and injective range implies operator surjective 168Ч169
Adjoint operator(s), closed range characterization 166Ч170
Adjoint operator(s), defining an embedding of 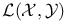 into into 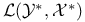 165 165
Adjoint operator(s), weak*-continuity of 166
Affine function(s) 215
Alaoglu, L. 124 125 see
Amir Ч Lindenstrauss Theorem 177 216
Amir, D. 176 219 see
Anderson, R.D. 218
Ando.T. 175
Approximation problem 184 219 220
Approximation property 218 321
Arzela Ч Ascoli theorem 182 186
Assent of an operator 192Ч193
Baire category theorem 76 78 124 221
Baire measure(s) 57
Baire sets 57
Banach Closed Graph Theorem see "Closed Graph Theorem"
Banach Homomorphism Theorem see "Open-Mapping Theorem"
Banach Isomorphism Theorem 63 80Ч81 222 226 291
Banach limit(s) 87Ч94
| Banach space(s) 18
Banach space(s) with Frechet differentiable norm 328Ч330
Banach space(s) with Gateaux differentiable norm 323Ч325
Banach space(s) with uniformly Frechet differentiable norm 330Ч333
Banach space(s), always contain subspace with basis 252
Banach space(s), always weak* dense in bidual 127Ч128
Banach space(s), criteria for containing subspace isomorphic to  284Ч285 284Ч285
Banach space(s), direct sums of 211Ч213
Banach space(s), grothendieck space 175 177 179 184 309
Banach space(s), nonreflexivity characterization 317Ч319
Banach space(s), norm achieving functionals on unit ball are dense 313Ч314
Banach space(s), reflexive exactly when closed subspaces with basis are 297
Banach space(s), smooth 323Ч325
Banach space(s), somewhat reflexive 257
Banach space(s), strictly convex (rotund) 325Ч328
Banach space(s), subreflexive 313
Banach space(s), uniformly convex 330Ч336
Banach space(s), uniformly smooth 330Ч336
Banach space(s), very smooth 330
Banach space(s), weak* sequential closure is norm closed in bidual 128Ч129
Banach space(s), weakly compactly generated 176
Banach space(s), weakly complete implies finite-dimensional 157
Banach space(s), weakly conditionally compact 254
Banach space(s), when isomorphic to Hilbert space 60Ч62
Banach Ч Alaoglu theorem 125 126 127 133 137 140 142 144 148 149 150 153 168 171 173 215 320 324
Banach Ч Alaoglu Theorem with respect to dual spaces 126
Banach Ч Mazur theorem 142 179 251 252 256 301
Banach Ч Steinhaus theorem 63 76Ч78 82 94 95 98 101 103 105 106 130 144 159 178 222 224 227 228 230 294 295 300
Banach's theorem 168 169 252 297
Banach's Weak Basis Theorem 222 229 230 239 296
Banach, Stefan 2 27 63 64 75 76 77 78 81 87 88 89 90 92 95 124 125 127 140 166 169 219 220 245 252 see "Banach "Banach "Banach "Banach's "Banach "Hahn
Bartle Ч Dunford Ч Schwartz Theorem 180 181
Bartle, R.G. 180 see
Basic selection principles see "Selection principles"
Basic sequence(s) 227Ч229
Basic sequence(s) and reflexivity 300Ч301
Basic sequence(s) in dual spaces 232
Basic sequence(s) in weakly null sequences 251Ч252
Basic sequence(s), Bessaga Ч Pelczynski criteria for selecting basic subsequence 249Ч251
Basic sequence(s), block 243Ч245
Basic sequence(s), equivalence of 240
Basic sequence(s), existence of with constant near one 252Ч252 253
Basic sequence(s), in weakly convergent sequences are bounded away from  251Ч252 251Ч252
Basic sequence(s), Mazur's criteria for selecting basic subsequence 247Ч249
Basic sequence(s), Rosenthal criteria for selecting basic subsequences and 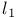 259Ч267 259Ч267
Basic sequence(s), when equivalent to basis 241Ч242
Basic sequence(s), when equivalent to unit vector basis of  244 244
Basis constant 232
Basis constant, existence of basic sequences with constant near one 252Ч253
Basis problem 219
Basis(es) 217 see "Shrinking "Boundedly
Basis(es) and complementation 242Ч243
Basis(es) and dense subsets 242
Basis(es) and subsequences 228Ч229
Basis(es) for James' space 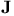 237Ч238 237Ч238
Basis(es) in reflexive spaces 286 297
Basis(es), associated coefficient functionals 220 225Ч226
Basis(es), Banach spaces always have subspace with 252
Basis(es), boundedly complete 294
Basis(es), characterization of for biorthogonal system 228Ч229
Basis(es), equivalence of weak and Schauder 222Ч222 230
Basis(es), equivalent bases 238Ч242
Basis(es), Haar system for ![$L_{p}([0,1])$](/math_tex/39a27923f4e71d2bf1e25ccf4c9c88e282.gif) 234Ч237 234Ч237
Basis(es), Hamel basis uncountable 221Ч222
Basis(es), internal characterization of 230Ч232
Basis(es), monotone 232 234
Basis(es), perturbation of 241Ч242
Basis(es), Schauder 220
Basis(es), Schauder system in C([0,1]) 233Ч234
Basis(es), shrinking 286
Basis(es), weak 220
Basis(es), weak*-Schauder 297 297
Bessaga Ч Pelczynski Selection Principle 220 249Ч251 252 254 257 269 282 285 304
Bessaga, C. 218 220 224 242 247 285 301 see
Best approximations 149Ч151
Bidual 72
Biorthogonal system(s) 226Ч229
Biorthogonal system(s) and expansion operators 226
Biorthogonal system(s), when yields basis or basic sequence 228 229
Bishop Ч Phelps theorem 270 310 311 312 313Ч314 330
Bishop, E. 310 313 322 see
Block basic sequence(s) 243Ч246
Block basic sequence(s) and shrinking bases 288Ч289
Block basic sequence(s) in  and and  243Ч245 243Ч245
Bochner, S. 180 181
Bohnenblust, H.F. 83
Bounded approximation property 218 219Ч220
Bounded multiplier Cauchy (convergent) series 277 see
Boundedly complete basis(es) 294
Boundedly complete basis(es) and shrinking yields reflexivity 297Ч299
Boundedly complete basis(es), examples 301
Boundedly complete basis(es), existence of guarantees being dual space 295Ч296
Boundedly complete basis(es), relationship with shrinking basis 294Ч295
Bourbaki, N. 127
Brooks, J.K. 77
C 32 89 100
c and matrix maps 96Ч99
c, dual 48Ч49
c, not isometrically isomorphic to  49 49
c, separable 34 71
Canonical injection j see "Natural injection"
Cantor set 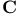 140Ч142 338Ч339 140Ч142 338Ч339
Cartesian produces(s) see "Produces"
Choquet, G. 150
Circled (balanced) set(s) 108 109Ч111
Circled hull 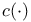 109 109
Clarkson, J.A. 270 334 336
Closed graph theorem 63 81Ч82 103 105 106 161 165 305
Coefficient functionals 220
Collins, H.S. 130
Compact operator(s) 181 182Ч186
Compact operator(s) and C([0,1]) 185Ч186 189
Compact operator(s) and the Riesz Ч Schauder theory 186Ч201
Compact operator(s) as operator ideal 183
Compact operator(s) on finite-dimensional spaces 182
Compact operator(s) on weakly sequentially compact spaces 254
Compact operator(s), between  -spaces 254Ч255 -spaces 254Ч255
Compact operator(s), exactly when adjoint compact 182
Compact operator(s), exactly when map bounded nets to convergent nets 184
Compact operator(s), is strictly cosingular 206
Compact operator(s), matrix form on 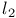 184Ч185 184Ч185
Compact operator(s), pointwise limit of on Grothendieck spaces 184
Compact operator(s), properties of 184Ч186
Compact operator(s), uniform limit of 184
Compactness and extreme points 146Ч148
Compactness, examples 189Ч190
Compactness, sequential, and conditionally countable 129 130Ч136
Comparable norms see "Norm(s)"
Complemented subspace(s) 161
Complemented subspace(s) in  and and  243Ч246 243Ч246
Complemented subspace(s),  is in any separable space 163 is in any separable space 163
Complemented subspaces problem 161
Completeness 18
Completeness, exactly when absolutely summable sequences are summable 27Ч28
Continuity of addition and scalar multiplication 21Ч22
Continuity, weak and weak* 158Ч159
Convex cone 311 312Ч313
Convex conjugates 29
Convex hull 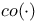 108Ч109 108Ч109
Convex set(s) 108 109Ч113
Convex set(s) and extreme points 144Ч146
Convex set(s) in locally convex spaces 121
Convex set(s), coincidence of weak and norm closure 122
Convex set(s), norm achieving functionals on 313Ч319
Convex set(s), support points and functionals for 311Ч313
Convex set(s), when weak* closed in dual 142Ч143
Conway, J.B. 87
Coordinate (projection) maps 5
Dabokov, R. 306
Daniell integral 11Ч16 58
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте




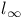
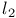
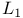
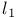 as dual of
as dual of 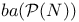
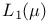


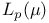
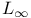
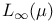
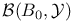
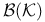
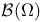
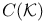 -space
-space 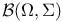
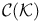
![$\mathcal{C}[0,1]$](/math_tex/5a7db169e0aa3351de258602580d65f182.gif)
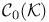
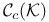
 -topology
-topology 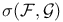 -topology, dual with respect to
-topology, dual with respect to 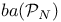
 )
) 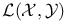 into
into 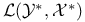
![$L_{p}([0,1])$](/math_tex/39a27923f4e71d2bf1e25ccf4c9c88e282.gif)