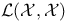|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Morrison T.M. Ч Functional Analysis: An Introduction to Banach Space Theory |
|
|
 |
| ѕредметный указатель |
Daniell integral, "Fatuou's Lemma" 14
Daniell integral, dominated convergence theorem 14
Daniell integral, functional 12
Daniell integral, measurability 15
Daniell integral, monotone convergence theorem 14
Daniell integral, vector lattice 12
Daniell, P.J. 2 11 see
Davis Ч Figel Ч Johnson Ч Pelczynski Factorization Theorem 214Ч215
Davis, W.J. 214 see
Day, M.M. 322 340
de Branges, L. 152
Dense subspaces see "Subspaces" "The
Descent of an operator 193
Diestel, J. 54 89 180 270 310 321 328 330
Dieudonne, J. 118 130 174
Differentiability of norm in dual and reflexivity 330
Differentiability of norm, in dual and reflexivity and smoothness 323Ч325
Differentiability of norm, in dual and reflexivity and support mappings 322Ч323
Differentiability of norm, in dual and reflexivity, Frechet 328 329Ч330
Differentiability of norm, in dual and reflexivity, Gateaux 323 324Ч325
Differentiability of norm, in dual and reflexivity, uniformly Frechet 330 331Ч333
Direct sum (product) of spaces 211Ч213
Direct sum decomposition 160Ч161
Direct sum decomposition, topological 161
Dixmier, X. 276
Dominated Convergence Theorem 14 35 58
Dor, L. 259
Dual space(s) 39 63Ч64
Dual space(s) in weak topology 120
Dual space(s), algebraic 64
Dual space(s), basis in reflexive spaces 297
Dual space(s), boundedly complete basis forces space to be 295Ч296
Dual space(s), calculation of, 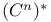 43 43
Dual space(s), calculation of, 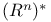 43 43
Dual space(s), calculation of, 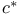 48Ч49 48Ч49
Dual space(s), calculation of, 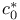 44Ч45 44Ч45
Dual space(s), calculation of, 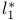 45Ч46 45Ч46
Dual space(s), calculation of, 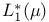 54 54
Dual space(s), calculation of, 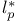 46Ч48 46Ч48
Dual space(s), calculation of, 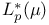 54Ч56 54Ч56
Dual space(s), calculation of, 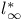 50 50
Dual space(s), calculation of, 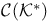 59Ч60 59Ч60
Dual space(s), coincidence of 48Ч49
Dual space(s), separable exactly when 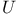 \mathcal{X}}$ weakly metrizable 137Ч139 \mathcal{X}}$ weakly metrizable 137Ч139
Dual space(s), separable implies bounded sequences in X have weak Cauchy subsequences 139
Dual space(s), separable implies underlying space is 71
Duality and dual systems 118Ч121
Dunford Ч Pettis operator 305 306 307 308
Dunford Ч Pettis operator, are operator ideal 307
Dunford Ч Pettis operator, characterization of when weakly compact operator is 306Ч307
Dunford Ч Pettis operator, examples 308
Dunford Ч Pettis operator, implies strictly singular 307Ч308
Dunford Ч Pettis property 305 306 309
Dunford Ч Pettis Property and strictly cosingular operators 309
Dunford Ч Pettis Property, examples 305Ч306
Dunford, N. 142 156 181 187 see "Dunford "Dunford
Dunford-Pettis theorem 176 181 306
Eberlein Ч Smulian theorem 124 129 130Ч136 137 142 144 170 216 300 307
Eberlein, W.F. 127 130 see
Eigenvalues and eigenvectors 198Ч201
Enflo, P. 219
Equivalent bases 238
Equivalent bases, basic sequences 240
Equivalent bases, characterization of 239Ч240
Essentially bounded function(s) 35
Exposed point(s) 326Ч327
Extreme point(s) 145 146Ч149
Extreme point(s) and best approximations 149Ч150
Extreme point(s) and smooth points 324
Extreme point(s) and supporting sets 146
Extreme point(s) in 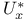 150 150
Extreme point(s) in 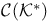 148Ч149 148Ч149
Extreme point(s), characterization of 145
Extreme point(s), existence of for compact convex sets 146Ч148
Extreme point(s), retrieving norm from 151
Faires, B. 330
Fatou's lemma 14
Figel, T. 214 see
Finite-dimensional space(s) and compact operators 182
Finite-dimensional space(s), all algebraically isomorphic 9
Finite-dimensional space(s), all topologically isomorphic 9Ч10
Finite-dimensional space(s), always complemented 161
Finite-dimensional space(s), compact sets in 10
Finite-dimensional space(s), compact unit ball 133
Finite-dimensional space(s), completeness 10
Finite-dimensional space(s), Hamel basis for 8
Finite-dimensional space(s), subspaces of 10
Frechet differentiability see "Differentiability"
Frechet space(s) 218
Frechet, M. 218 see "Frechet
Fredholm operator theory 187 197
Friedberg, S.H. 8
Fubini's theorem 186
Functional(s) 39
Functional(s), coefficient 220
Functional(s), determining nbhds of  in locally convex spaces 113Ч114 in locally convex spaces 113Ч114
Functional(s), haif-spaces determined by 121
Functional(s), linear dependence of 119Ч120
Functional(s), Minkowski 114
Functional(s), separating in locally convex spaces 115Ч116 120Ч121
Functional(s), separating in normed linear spaces 111Ч112
Gantmacher Ч Nachamura Theorem 173 174 177 182
Gantmacher, V. 173 see
Gateaux differentiability see "Differentiability"
Gelfand, I.M. 87
Giles, J.R. 322
Goldstine's Theorem 127Ч128 138 170 171 173 295 298
Goldstine, H.H. 128 see
Grothendieck space(s) 175 177 179 184 309
Grothendieck space(s), equivalents, 177Ч179
Grothendieck space(s), pointwise limit of compact operators on 184
Grothendieck, A. 130 174 175 218 275 280 305 309 see
Grymblyum Ч Nikol'skii Theorem 230Ч232 234 237 238 243 249 253 265
Haar measure(s) 90Ч94
Haar system for ![$L_{p}([0,1])$](/math_tex/39a27923f4e71d2bf1e25ccf4c9c88e282.gif) 234Ч237 234Ч237
Haar system for ![$L_{p}([0,1])$](/math_tex/39a27923f4e71d2bf1e25ccf4c9c88e282.gif) and biorthogonal functionals 236Ч237 and biorthogonal functionals 236Ч237
Haar system for ![$L_{p}([0,1])$](/math_tex/39a27923f4e71d2bf1e25ccf4c9c88e282.gif) , boundedly complete 301 , boundedly complete 301
Haar system for ![$L_{p}([0,1])$](/math_tex/39a27923f4e71d2bf1e25ccf4c9c88e282.gif) , shrinking 290 , shrinking 290
Haar, A. 90 92 234 see 1])$"/>
Hahn Ч Banach theorem 34 51 63 64 65Ч68 71 81 82 83Ч84 86 87 88 89 94 105 106 111Ч112 115 129 132 138 139 150 151 153 157 162 163 166 167 169 203 221 231 244 251 293 312 339
Hahn Ч Banach Theorem in locally convex spaces 115Ч116
Hahn Ч Banach Theorem, complex 83Ч84
Hahn Ч Banach Theorem, extension form 65Ч68
Hahn Ч Banach Theorem, separation form 111Ч112
Hahn, H. 64 104 277 see
Halmos, P.R. 35
Hamel basis 28 64 162 164 203 217 220 221 222
Hamel basis, uncountable in complete, infinite dimensional spaces 221Ч222
Hausdorff maximality principle 65 68 147
Heine Ч Borel theorem 10 125
Helly's theorem 63 104Ч105 318
Helly, E. 104 see
Hermann, R. 257
Hilbert cube 189
Hilbert space(s) 60Ч62 89 162Ч163 184Ч185 187 327 339Ч340
Hilbert space(s) and uniform convexity 339Ч340
Hilbert space(s), complemented subspaces 162Ч163
Hilbert Ч Schmidt operators 186
Hilbert, D. 181Ч184 see
Hoelder's inequality 29 30 31 47 54 103 186
Hoelder, E. see "Holder's Inequality"
Holub, J.R. 321
Homeomorphism 22
Hsieh, M. 334
Huff, R.E. 312
Idempotent 159
Insel, A.J. 8
integral see "Daniell integral"
Internal point(s) 109
James' space 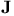 73Ч75 220 232 237 257 258 270 290 292 293 299 301 302 303 73Ч75 220 232 237 257 258 270 290 292 293 299 301 302 303
| James' space 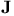 , basis for 237Ч238 , basis for 237Ч238
James' space 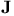 , basis for, not boundedly complete 301 , basis for, not boundedly complete 301
James' space 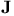 , basis for, shrinking 290 , basis for, shrinking 290
James' space 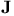 , is isometrically isomorphic to dual 301Ч303 , is isometrically isomorphic to dual 301Ч303
James' space 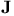 , is of codimension one in bidual 75 292Ч294 , is of codimension one in bidual 75 292Ч294
James' space 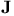 , is somewhat reflexive 257Ч258 , is somewhat reflexive 257Ч258
James' space 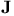 , nonreflexivity 299 , nonreflexivity 299
James' theorem 297Ч299 300 330 334
James, R.C. 73 75 220 237 270 286 290 294 297 310 313 314 317 319 322 387 see "James'
Johnson, W.B. 214 219 see
Jordan decomposition 55 60
Kadec, M.I. 218 334 337 338
Kakutani, S. 127 see
Karlin, S. 219
Kato, T. 202
Kershner, R. 93
Klee, V. 313 317 327
Knopp Ч Lorentz Summability Theorem 63 101Ч102
Knopp, K. 63 see
Koethe, G. 24 334
Krein Ч Milman theorem 107 127 142 146Ч148 149 151 153
Krein Ч Milman Ч Rutman theorem 242
Krein Ч Smulian Theorem 142Ч143 143Ч144 168 169 170 177 178
Krein Ч Smulian Theorem, closed convex hull of closed convex sets is weakly compact 143Ч144
Krein Ч Smulian Theorem, when convex sets are weak*-closed in 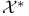 142Ч143 142Ч143
Krein, M.G. 144 146 148 241 242 see "Krein
Kronecker delta function, 225
Lifting problem 32
Lindenstrauss, J. 161 162 176 216 219 252 see
Linear operator(s) see "Operator(s)"
Linear projection(s) see "Projection(s)" "Complemented
Linear topological space(s) see "Topological vector space(s)"
Liouville's theorem 85
Liouville, J. 85
Lipschitz function(s) 52
Lipschitz measures 52 180 see \mathcal{X})$"/>"
Locally convex space(s) 113Ч114
Locally convex space(s) as a product of Banach spaces 116Ч117
Locally convex space(s), existence of nonzero functionals on 113 121
Locally convex space(s), quasi-complete 319
Locally convex space(s), weak dual of 121
Locally convex topology 119
Lohman, R.H. 247
Lorentz, G.G. 63 see
Lusternick 241
Matrix maps 95Ч103
Matrix maps, conservative 100
Matrix maps, map bounded sequences to bounded sequences 97Ч98
Matrix maps, map convergent sequences to convergent sequences 98Ч99
Matrix maps, map summable sequences to summable sequences 102
Matrix maps, regular (permanent) 100
Mazur Selection Principle 247Ч248
Mazur's theorem 122 132 136 139 144 178 229 231 280 286 320 330
Mazur, S. 95 122 140 143 173 247 see "Mazur's "Mazur's
McArthur, C.W. 218 280
McShane, E.J. 334
McWilliams, R.D. 128 129
Mean value theorem 29
Measure(s), Baire 57
Measure(s), counting 56
Measure(s), existence of invarient 89Ч94
Measure(s), Lizschitzean 52
Measure(s), metric outer 90 93
Milman, D.P. 144 146 148 242 257 333 see "Krein "Krein
Milman, V.D. 257
Minkowski (gauge) functional(s) 109 110 111 112 113 114 116 212
Minkowski (gauge) functional(s), when continuous 114Ч116 212
Minkowski's inequality 30 31 73 74 236
Minkowski, H. 109 see "Minkowski
Minusinski, J. 77
Modulus of convexity 331 337 338
Modulus of convexity of Hilbert space 340
Monomorphism 202
Monotone Convergence Theorem 35 55
Moore, T.O. 140
Munroe, J.R. 265
Nagumo, M. 85
Nakamura, M. 173 see
Natural injection j 72 127Ч128 133 138Ч139 170Ч171 286
Nearest point(s) 326Ч327
Nets 3 5
Nets, weak and weak* convergence of 156
Neumann series of operators 190Ч191
Neumann, G 190
Nordlander, G. 340
Norm 9 17Ч18
Norm achieving functionals and reflexivity 313 317Ч319
Norm achieving functionals and weak compactness 319Ч321
Norm, 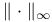 20 20
Norm, comparable 80 81
Norm, defined by functionals 70
Norm, Frechet differentiable 328Ч330
Norm, Gateaux differentiable 323Ч325
Norm, norm topology 22
Norm, operator (uniform) 39
Norm, positive homogeneous 18
Norm, seminorm 24
Norm, subadditive 18
Norm, uniformly Fredchet differentiable 330Ч333
Norm, variational 50
Normed linear space(s) 18
Normed linear space(s), reflexive always complete 75
Norming set 129 247
Norming set, when have countable one in dual 129
Null space (kernel) of operator 160
Null space (kernel) of operator and complementation 195
Null space (kernel) of operator, properties of 194Ч198
Open-Mapping Theorem 63 78Ч80 81 82 103 104 105 117 167 208 289
Operator ideal(s) 171Ч172 183 184 193 205 207 208 307
Operator ideal(s) in reflexive  -spaces 184 -spaces 184
Operator ideal(s), compact operators 183
Operator ideal(s), Dunford Ч Pettis operators 307
Operator ideal(s), strictly cosingular operators 208Ч209
Operator ideal(s), strictly singular operators 205
Operator ideal(s), weakly compact operators 172
Operator(s) 37Ч38 see "Compact
Operator(s) with closed range 166Ч169 187Ч188
Operator(s), adjoint 164Ч170
Operator(s), almost open 79
Operator(s), ascent of 192Ч193
Operator(s), bounded and continuous basic equivalences 38
Operator(s), continuous in locally convex spaces 114Ч115
Operator(s), convergence of on dense subspaces 99
Operator(s), descent of 193
Operator(s), Dunford Ч Pettis 305 306Ч310
Operator(s), eigenvalues and eigenvectors of 198
Operator(s), extension from dense subspace 40Ч41 42
Operator(s), finite rank 179
Operator(s), graph of 81
Operator(s), into 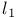 or on or on  182Ч183 182Ч183
Operator(s), linear 37
Operator(s), nilpotent 197
Operator(s), noncompact with compact square 196
Operator(s), null space (kernel) 160
Operator(s), open map 24
Operator(s), properties of mill space and range 194Ч198
Operator(s), range of 159
Operator(s), reflexivity of 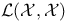 321 321
Operator(s), semivariation of 180
Operator(s), spectrum of 200Ч201
Operator(s), unconditionally converging 304Ч305
Operator(s), when quotient 170
Orlicz Ч Pettis theorem 280Ч282
Orlicz, W. 95 269 277 280 see
Parseval's identity 162
Pelczynski, A. 210 214 218 219 220 224 241 243 245 246 247 285 299 300 301 304 309 see
Pettis' theorem 282
Pettis, B.J. 181 269 277 280 282 333 see "Orlicz "Pettis'
Phelps, R.R. 310 313 322 see
Phillips' Lemma 270Ч274 275 276 277
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



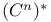
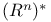
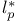
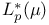
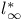
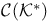
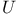 \mathcal{X}}$ weakly metrizable
\mathcal{X}}$ weakly metrizable 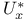
 in locally convex spaces
in locally convex spaces ![$L_{p}([0,1])$](/math_tex/39a27923f4e71d2bf1e25ccf4c9c88e282.gif)
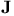
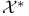
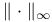
 -spaces
-spaces 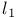 or on
or on