|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Morrison T.M. Ч Functional Analysis: An Introduction to Banach Space Theory |
|
|
 |
| ѕредметный указатель |
Phillips's theorem 275
Phillips, R.S. 175 269 270 275 see "Phillip's
Pietsch operator ideal see "Operator ideal"
Pietsch, A. 171 see
Pitt Ч Rosenthal Theorem 254Ч255
Pitt, H.R. 254 see
Principal of Uniform Boundedness see "Banach Ч Steinhaus Theorem"
Product(s) (Cartesian) and the product topology 4Ч8
Product(s) (Cartesian) and the product topology, continuity in 6
Product(s) (Cartesian) and the product topology, fundamental system of neighborhoods 5Ч6
Product(s) (Cartesian) and the product topology, local base 5
Product(s) (Cartesian) and the product topology, tie to weak topology 7Ч8
Projection(s) 159Ч163
Projection(s) and complemented subspaces 160Ч161
Projection(s) and direct sums 212Ч213
Pseudonorm see "Seminorm"
Ptak, V. 130
Quotient(s) 23Ч25
Quotient(s), dual of space 51
Quotient(s), exactly when adjoint is isomorphism 170
Quotient(s), map 24 78
Quotient(s), properties of, 24Ч25
Quotient(s), space 24
Radon Ч Nikodym theorem 54 55 103 277 321 334
Range of operator 159
Range of operator and complementation 195Ч196
Range of operator, closed, implications of 166Ч170
Range of operator, dense 168
Range of operator, properties of 194Ч198
Range of operator, reformulation of range when closed 169
Reflexivity 72
Reflexivity and basic sequences 300Ч301
Reflexivity and factoring weakly compact operators 214Ч216
Reflexivity and Frechet differentiability in dual 330
Reflexivity and nearest points for convex set 326Ч327
Reflexivity and norm achieving functionals 317Ч319
Reflexivity and smootlmess, support mappings 330
Reflexivity and strict convexity, smoothness 327 329
Reflexivity and unconditionally convergent series 280Ч282
Reflexivity and weakly compact sets 216
Reflexivity for 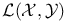 321 321
Reflexivity, basis(es) for dual 297
Reflexivity, basis(es), characterization of 300Ч301
Reflexivity, basis(es), coefficient functionals basis for dual 286
Reflexivity, completeness in 75
Reflexivity, exactly when closed subspaces are, and exactly when bounded sequences have weak convergent subsequences 136Ч136 137
Reflexivity, exactly when closed subspaces with bases are 299Ч300
Reflexivity, if dual uniformly smooth 334
Reflexivity, is uniformly convex 333Ч334
Retherford, J.R. 290
Riesz representation theorem 54Ч56
Riesz Ч Kakutani Representation Theorem 59Ч60 144 180
Riesz Ч Schauder theory 155 184 186Ч201
Riesz's Lemma 10Ч11
Riesz, F. 2 10 104 181 187 see "Riesz "Riesz "Riesz
Rosenthal Selection Principle 259Ч267
Rosenthal's Theorem 259Ч267 283 300
Rosenthal, A. 254 see
Rosenthal, H.P. 219 220 256 258 260 261 266 see "Rosenthal's
Rotundity see "Strict convexity"
Royden, H.L. 12 35
Rutman, M.A. 242 see
Saks, S. 76 277
Schaefer, H.H. 24
Schauder basis(es) see "Basis(es)"
Schauder system for C([0,1]) 233Ч234
Schauder's theorem 182 183 184 193
Schauder, J. 78 182 187 217 233 235 see 1])" "Schauder's
Schur property 182 259
Schur Property, 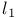 has 276 has 276
Schur Property, closed subspace contains copy of 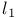 259Ч260 259Ч260
Schur space(s) 254
Schur's theorem 269 276 305
Schur, J. 276 see "Schur "Schur's
Schwartz, J.T. 142 156 187
Schwartz, L. 130
Seever, G.L. 175
Selection principles, Bessaga Ч Pelczynski 249Ч251
Selection principles, Mazur 247Ч248
Selection principles, Rosenthal 259Ч267
Seminorm 24 110 118Ч119
Separability 33
Separability as quotients of 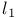 103Ч104 103Ч104
Separability in 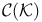 or or 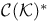 157Ч158 157Ч158
Separability, all linearly isometric to subspace of C([0,1]) 160
Separability, are weakly compactly generated 176
Separability, bounded sequences have weak* convergent subsequences in dual 140
Separability, dual is implying space is 71
Separability, exactly when 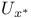 weak*-metrizable 137Ч139 weak*-metrizable 137Ч139
Series, coincidence of weak and norm subseries convergence 280Ч282
Series, equivalence of unconditionally Cauchy (convergent), unordered Cauchy (convergent), subseries Cauchy (convergent), and bounded multiplie Cauchy (convergent) 277Ч280
Series, weakly unconditionally convergent, 282Ч283
Set(s),  -bounded 57 -bounded 57
Set(s),  -compact 57 -compact 57
Set(s), absorbing 109
Set(s), annihilator of 151
Set(s), Baire 57
Set(s), bounded 37
Set(s), circled (balanced) 108
Set(s), closed linear span ![$[\cdot]$](/math_tex/fde0b03b2aeffe093a356627faffa57982.gif) 71 71
Set(s), closure (norm) 23
Set(s), convex 108
Set(s), distance from point to 68
Set(s), norming 129 247
Set(s), polar of 143
Set(s), radial at x 109
Set(s), total 129
Set(s), weak* bounded 157
Shrinking basis(es), 286
Shrinking basis(es), and boundedly complete yields reflexivity 297Ч299
Shrinking basis(es), boundedly complete basis, relationship with 294Ч295
Shrinking basis(es), equivalences and bounded sequences 288Ч289
Shrinking basis(es), exactly when coefficient functionals are basis for dual 287Ч288
Shrinking basis(es), examples 289Ч290
Shrinking basis(es), generates an equivalent norm in dual 290Ч292
Shrinking basis(es), of James' space 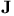 290 290
Silverman Ч Toepliz Summability Theorem 63 100Ч101
Silverman, L.L. 63 100 see
Singer, I. 150 246 296 300
Smoothness 323 324Ч325
Smoothness and Gateaux differentiability 324Ч325
Smoothness and strict convexity 323
Smoothness, reflexivity and support mappings 330
Smoothness, very smooth 330
Smulian, V.L. 127 130 131 142 328 see "Krein
Sobczyck, A. 83 163
Somewhat reflexive 257
Somewhat reflexive, James' space is 257Ч258
Spectral theory 198Ч210
Spectral theory, spectrum of an operator 200Ч201
Spence, L.E. 8
Steinhaus, H. 75 76 77 see
Stone Ч Cech compactification 26
Stone Ч Weierstrass theorem 149 151 152Ч153
Stone's theorem 15Ч16 58
Stone, M.H. 14 15 see "Stone's
Strict convexity (rotundity) 325 326Ч328
Strict convexity (rotundity) and reflexivity 327
Strict convexity (rotundity) and smoothness 327
Strict convexity (rotundity), metric characterization of 325Ч326
Strictly cosingular operator(s) 206 207Ч210
| Strictly cosingular operator(s) and compact operators 206
Strictly cosingular operator(s) and the Dunford-Pettis property 309
Strictly cosingular operator(s) and weakly compact 206
Strictly cosingular operator(s), adjoint of 209Ч210
Strictly cosingular operator(s), operator ideal 207Ч209
Strictly singular operator(s) 201 202Ч210
Strictly singular operator(s) and compact operators 202
Strictly singular operator(s) and weakly compact operators 209Ч210
Strictly singular operator(s) on 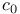 or or 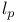 202 202
Strictly singular operator(s), adjoint of 209
Strictly singular operator(s), characterization of 205
Strictly singular operator(s), if Dunford Ч Pettis 307Ч308
Strictly singular operator(s), implies unconditionally converging 304Ч305
Strictly singular operator(s), operator ideal 205Ч206
Strictly singular operator(s), when largest two-sided ideal 308Ч309
Subseries Cauchy (convergent) 277 see
Subseries Cauchy (convergent), coincidence of weak and norm 280Ч282
Subspace(s) and reflexivity 136Ч137 299Ч300
Subspace(s) of finite codimension 207
Subspace(s) of finite deficiency and compact operators 202Ч204
Subspace(s), always exist with basis 252
Subspace(s), closure 70
Subspace(s), codimension of 292
Subspace(s), dual of 51
Subspace(s), extension of linear functionals on 68
Subspace(s), is subspace 22
Subspace(s), maximal closed subspaces are isomorphic 299
Subspace(s), separation from points outside 69
Subspace(s), when dense 70
Subspace(s), when dense, dense examples 42 50 53
Subspace(s), when weak* closed in dual 143
Summable sequences 27
Support mapping(s) on unit sphere 322Ч323
Support mapping(s) on unit sphere and reflexivity 330
Support mapping(s) on unit sphere and smoothness, Gateaux differentiability 324Ч325
Support mapping(s) on unit sphere and uniform smoothness, uniform convexity of dual 332Ч333
Support mapping(s) on unit sphere, Frechet differentiability 329
Supporting set(s) 146
Supporting set(s) of a measure 152
Taylor, A.E. 11 187
Toeplitz, O. 63 100 see
Topological dual space(s) see "Dual space(s)"
Topological vector space(s) 21 112
Total set(s) 70 129
Total set(s), when countable in dual 129
Totally incomparable spaces 255
Totally incomparable spaces, 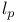 -spaces 256 -spaces 256
Totally incomparable spaces, sum of always closed 256Ч257
Tsing, Nam-Kiu 221
Tychonoffs theorem 125
Tzafriri, L. 161 162 163 252
Uhl, J.J. 54 180
Unconditionally Cauchy (convergent) series 211 see
Unconditionally Cauchy (convergent) series and uniform convexity 338Ч339
Unconditionally converging operator(s) 304
Unconditionally converging operator(s), examples 305Ч306
Unconditionally converging operator(s), if strictly singular 304Ч305
Uniformly convex 331 332Ч339
Uniformly convex and modulus of convexity 337
Uniformly convex and unconditionally convergent series 338Ч339
Uniformly convex of 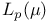 -spaces 336Ч337 -spaces 336Ч337
Uniformly convex, characterization 331 332Ч333
Uniformly convex, dual characterization 332Ч333
Uniformly convex, is reflexive 333Ч334
Uniformly Frechet differentiable norm see "Differentiability"
Uniformly smooth 330 331
Uniformly smooth, characterization 332Ч333
Uniformly smooth, if dual is then reflexive 334
Unit ball 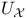 36 36
Unit ball 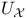 and extreme points in dual 150 and extreme points in dual 150
Unit ball 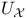 , compact exactly when finite-dimensional 133 , compact exactly when finite-dimensional 133
Unit ball 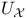 , dual ball weak*-metrizable exactly when space separable 137Ч139 , dual ball weak*-metrizable exactly when space separable 137Ч139
Unit ball 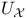 , nonweak compactness of 125Ч126 , nonweak compactness of 125Ч126
Unit ball 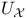 , norm achieving functionals are dense 313Ч314 , norm achieving functionals are dense 313Ч314
Unit ball 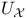 , support mappings on 322Ч323 , support mappings on 322Ч323
Unit ball 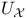 , weak* compactness of dual ball 125 , weak* compactness of dual ball 125
Unit ball 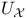 , weak* denseness in bidual unit ball 127Ч128 , weak* denseness in bidual unit ball 127Ч128
Unit ball 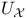 , weakly metrizable exactly when dual separable, 137Ч139 , weakly metrizable exactly when dual separable, 137Ч139
Unit sphere 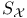 37 37
Unit sphere 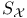 , nearness to closed subspaces with elements of , nearness to closed subspaces with elements of 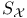 10Ч11 10Ч11
Unordered Cauchy (convergent) series 277 see
Urysohn's lemma 148
Vector lattice(s) 12
Vector measure(s) 53Ч54
Vector measure(s), coincidence of weak and strong 282
Veech, W.A. 163
Very smooth 330
Vitali Ч Hahn Ч Saks Theorem 277
Vladimorskii, W. 207
Weak basis(es) see "Basis(es)"
Weak compactness and norm achieving functionals 319Ч319 321
Weak compactness of unit ball characterizes reflexivity 127
Weak compactness, affinely homeomorphic to subset of reflexive space 216
Weak compactness, implies closed convex hull is weakly compact 143Ч144
Weak compactness, is closed and bounded 126 130
Weak compactness, metrizable in separable spaces 131
Weak topology 117Ч121 122 123 124
Weak topology, continuity and boundedness in, 158Ч159
Weak topology, convergence of nets 123
Weak topology, induced by a collection of functions 7Ч8
Weak topology, nonmetrizability of 123Ч124
Weak topology, open sets in 123
Weak topology, relativized 131Ч132
Weak topology, sets are weak bounded exactly when norm bounded 130
Weak topology, weakly compact sets 126
Weak* compactness of unit ball 125
Weak* topology 123 124
Weak* topology, continuity and boundedness in 158Ч159
Weak* topology, convergence of nets 124
Weak* topology, nonmetrizability of 124
Weak* topology, weak* bounded exactly when bounded 157
Weakly compact operator(s) 170 171Ч181
Weakly compact operator(s) and strictly singular operators 309
Weakly compact operator(s) in and on special spaces 176Ч181
Weakly compact operator(s) on 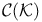 -spaces 310 -spaces 310
Weakly compact operator(s), characterization of 215
Weakly compact operator(s), exactly when 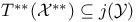 171 171
Weakly compact operator(s), exactly when adjoint is weak*-weak continuous 172Ч173
Weakly compact operator(s), exactly when adjoint is weakly compact 173
Weakly compact operator(s), examples of nonweakly compact 174
Weakly compact operator(s), operator ideal 172
Weakly compact operator(s), some properties of 174
Weakly compact operator(s), when Dunford Ч Pettis 306Ч307
Weakly compactly generated space(s) 176 177
Weakly compactly generated space(s), characterization of 216
Weakly sequentially compact 254
Weakly sequentially compact, compact operators on 254
Weakly sequentially complete 157 282
Weakly sequentially complete, 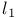 is 276Ч277 is 276Ч277
Weakly sequentially complete, is reflexive or has subspace isomorphic to 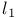 259 259
Weakly sequentially complete, unconditional convergence of series in 280Ч282
Weakly subseries convergent series have subsequence converging to zero in norm 281
Weakly unconditionally convergent series (w.u.c. series) 283Ч285
Weakly unconditionally convergent series (w.u.c. series), basic sequence equivalent to unit vector basis of 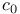 284Ч285 284Ч285
Weierstrass' theorem 33 42
Weierstrass, K. see "Weierstrass' Th Stone Ч Weierstrass Theorem"
Weil, A. 189
Whitley, R.J. 130
Willard, S. 26 140 265
Yosida, K. 187
Zippin, M. 219
Zorn's lemma 8 312
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



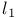 has
has 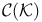 or
or 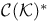
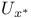 weak*-metrizable
weak*-metrizable  -bounded
-bounded ![$[\cdot]$](/math_tex/fde0b03b2aeffe093a356627faffa57982.gif)
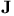
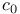 or
or 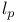
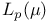 -spaces
-spaces 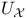
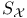
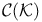 -spaces
-spaces