|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Pedicchio M. C., Tholen W. — Categorical Foundations: Special Topics in Order, Topology, Algebra, and Sheaf Theory |
|
|
 |
| Предметный указатель |
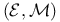 -closed class of morphisms III.112 -closed class of morphisms III.112
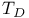 -space II.66 -space II.66
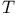 -algebra VI.275 -algebra VI.275
 -biquotient map III.150 -biquotient map III.150
 -closed embedding III.112 -closed embedding III.112
 -closed morphism III.112 -closed morphism III.112
 -closure III.156 -closure III.156
 -compact object III.119 -compact object III.119
 -compactification III.133 -compactification III.133
 -cowellpowered subcategory III.159 -cowellpowered subcategory III.159
 -dense morphism III.113 -dense morphism III.113
 -discrete object III.139 -discrete object III.139
 -exponentiable morphism III.148 -exponentiable morphism III.148
 -exponentiable object III.151 -exponentiable object III.151
 -final morphism III.143 -final morphism III.143
 -Hausdorff object III.126 -Hausdorff object III.126
 -open morphism III.136 -open morphism III.136
 -open subobject III.137 -open subobject III.137
 -perfect morphism III.129 -perfect morphism III.129
 -proper morphism III.118 -proper morphism III.118
 -quotient morphism III.145 -quotient morphism III.145
 -separated morphism III.124 -separated morphism III.124
 -separated object III.126 -separated object III.126
 -Tychonoff morphism III.132 -Tychonoff morphism III.132
 -Tychonoff object III.131 -Tychonoff object III.131
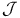 -closed arrow VII.337 -closed arrow VII.337
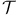 -Models, category of VI.270 -Models, category of VI.270
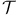 -sheaf VII.329 -sheaf VII.329
2-dimensional exponent VIII.390
2-functor I.38
Abelian category IV.203
Abelian group, internal IV.191
Abelian group, torsion-free IV.180
Abelian object IV.194
Absolute coequalizer V.224
Absolutely  -closed morphism III.132 -closed morphism III.132
Absolutely  -closed object III.131 -closed object III.131
Abstractly finite object VI.289
Additive category IV.200
Additive category, regular VI.294
Adjoint, left I.12 15
Adjoint, right I.12 15
Adjunction I.6 12 15
Adjunction, Isbell conjugation I.38
Alexandroff topology I.35
Algebra of an endomorphism V.254
Algebra, boolean I.23
Algebra, Eilenberg — Moore V.217
Algebra, Heyting I.24
Algebra, Lie V.246
Algebra, separable VIII.399
Algebra, split VIII.399
Algebra, trivial VIII.399
Algebraic 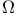 -set III.131 -set III.131
Algebraic category VI.270
Algebraic theory VI.270
Algebraic variety IV.179
Antisymmetric relation I.16
Arrow, 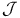 -closed VII.337 -closed VII.337
Arrow, cartesian IV.168
Arrow, fibrant IV.168
Axiom 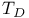 II.66 II.66
Barr — Kock Theorem IV.176
Barr-exact category IV.179
Beck — Chevalley Property III.145
Beck’s criterion V.228
Bi-quotient map VIII.362
Bicategory I.12
Bidense morphism VII.324
Biproduct IV.201
Birkhoff — Witt Theorem V.247
Boolean algebra I.23
Boolean topos I.7
Booleanization II.65
Bundle VIII.395
Bundle, induced VIII.395
Bundle, locally trivial fibre, with fibre F VIII.402
Bundle, locally trivial, of topological spaces VIII.401
Bundle, split VIII.395
Bundle, trivial VIII.395
Bundle, trivial, of topological spaces VIII.401
Calculus of fractions, left VII.325
Calculus of relations VII.346
Cancellation property, strong right VIII.364
Cartesian arrow IV.168
Cartesian closed category VII.329
Category I.5
Category of 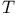 -algebras VI.275 -algebras VI.275
Category of 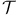 -Models VI.270 -Models VI.270
Category of Abelian groups III.117
Category of categories I.8
Category of complete atomic Boolean algebras V.231
Category of fractions VII.325
Category of frames II.52 V.230
Category of graphs V.231
Category of internal abelian groups IV.192
Category of internal groups IV.191
Category of locales II.54 III.138
Category of meet-semilattices II.70
Category of presheaves IV.179
Category of sets IV.179
Category of shapes V.242
Category of small categories IV.180
Category of topological groups IV.180
Category of topological spaces III.137 IV.180
Category with enough regular projectives VII.336
Category, abelian IV.203
Category, additive IV.200
Category, additive regular VI.294
Category, algebraic VI.270
Category, Barr-exact IV.179
Category, cartesian closed VII.329
Category, comma III.117
Category, distributive VII.343
Category, exact V.234 VI.281
Category, extensive III.115 VII.342
Category, fibre-determined III.146
Category, finitely extensive III.115
Category, Kleisli V.220 251
Category, lextensive VII.342
Category, linear IV.200
Category, locally finitely presentable VI.298
Category, Maltsev IV.189 VI.290
Category, monadic V.222
Category, monadic, over Set V.234
Category, monoidal V.215
Category, multi-sorted VI.277
Category, naturally Maltsev VI.294
Category, non-associative VIII.392
Category, pointed IV.172
Category, protomodular IV.184 VI.294
Category, quasi-algebraic VI.288
Category, regular IV.177 VI.279 VII.336
Category, S-sorted algebraic VI.277
Category, skeletal I.10
Category, strict monoidal V.258
Chasles relation IV.191 194
Chu space, extensive Boolean III.117
Clementino — Tholen Theorem III.141
Clopen map III.115
Closed localic map II.83
Closed map III.112
Closed sublocale II.62
Closed under limits III 109
Closure of a sublocale II.64
Closure operator III.156
Closure operator, hereditary III.156
Closure operator, idempotent III.156
Closure operator, universal III.114 VII.323
Closure, down- II.70
| Co-dense localic map II.82
Co-Frobenius Identity II.87
Coarse relation IV.168
Cocycle condition, Grothendieck’s VIII.383
Coequalizer, absolute V.224
Coequalizer, reflexive VI.274
Coherence, classical V.242
Cokernel IV.172
Colimit, weak VI.292
Comma category III.117
Commutative monad V.257 261
Commutative monoid V.262
Compact clement II.89
Compact locale II.83
Compactification of a locale II.94
Compactification, Stone — Cech II.93 III.134 159
Comparison functor VI.276
Comparison functor, Grothendieck’s VIII.385
Compatible family VII.316
Complement I.23
Complement, pseudo- I.24 II.53
Complete filter II.56
Complete Heyting algebra II.53
Complete Heyting homomorphism II.84
Complete Heyting lattice I.42
Complete lattice, (CCD) I.44
Complete lattice, (CD) I.44
Complete lattice, completely distributive I.44
Complete lattice, constructively completely distributive I.44
Complete ordered set I.36
Complete ring of sets I.46
Completely distributive complete lattice I.44
Completely distributive complete lattice, constructively I.44
Completely prime filter II.56
Completely regular locale II.78
Completion, exact VI.295 VII.351
Composite relation I.11
Congruence II.61
Conjunctive locale II.77
Connected object VII.353
Continuous lattice II.95
Continuous section VII.315
Coproduct completion VII.339
Coproduct in Frm II.71
Coreflective full suborder I.32
Coreflector I.32
Cosmos theory VIII.390
Cover of a locale II.83
Cover, regular projective VII.336
Covering space VIII.402
Covering, etale VIII.399
Day — Kelly Theorem III.152
de Morgan law II.53
Decidable object III.128
Dense factorization II.65
Dense generator VI.300 VII.347
Dense localic map II.64
Dense sublocale II.64
Dense subobject VII.324
Descent data VIII.375
Descent map III.150
Descent morphism VIII.375
Descent theory, elementary VIII.375 381
Descent theory, global VIII.375
Descent theory, Grothedieck’s (original) VIII.381
Descent theory, monadic VIII.381
Diamond Principle V.240
Difunctional relation VI.291
Direct sum IV.201
Discrete order I.29
Discrete ordered set I.19
Discrete relation IV.168
Distributive category VII.343
Distributive lattice I.23
Distributive, infinite, law II.52
Down-interior I.31
Downset I.30
Downset functor II.70
Duality, Gelfand II.51
Duality, Hofmann — Lawson II.97
Effective descent morphism V.237 VIII.375
Effective discrete fibration of equivalence relations VIII.368
Effective equivalence relation IV.169 VI.281 VIII.367
Effective projective object VI.303
Eilenberg — Moore algebra V.217
Eilenberg — Moore comparison functor V.222
Eilenberg — Moore object V.253
Element, compact II.89
Element, finite II.89
Element, R-related I.11
Element, R-saturated II.66
Element, regular VII.334
Elementary topos I.5 VII.330
Embedding III.109
Embedding,  -closed III.112 -closed III.112
Enough regular projectives VII.336
Epic pair of arrows, jointly strongly IV.185
Epimorphism VIII.360
Epimorphism, extremal VIII.361
Epimorphism, normal VIII.360
Epimorphism, regular IV.171 VIII.360
Epimorphism, split IV.171 VIII.360
Epimorphism, stably extremal VIII.365
Epimorphism, stably regular VIII.361
Epimorphism, stably strong VIII.361
Epimorphism, strong IV.170 VIII.361
Equivalence functor I.10
Equivalence relation IV.167 VI.280
Equivalence relation, effective IV.169 VI.281 VIII.367
Equivalence relation, stably effective VIII.369
Essentially algebraic theory VI.299
Etale covering VIII.399
Etale map VII.315
Exact category V.234 VI.281
Exact completion VI.295 VII.351
Exact diagram VIII.368
Exact fork IV.178
Exact sequence IV.198
Extension (in homological algebra) VIII.396
Extension space VIII.401
Extension, finite separable VIII.398
Extension, Galois, of a commutative ring VIII.399
Extensive category III.115 VII.342
Extremal epimorphism VIII.361
Extremal epimorphism, stably VIII.365
Extremal monomorphism II.60
Factorization system III.107
Factorization system, orthogonal III.107
Factorization system, proper III.107
Factorization theorem II.68
Factorization, antiperfect-perfect III.135
Factorization, canonical V.262
Factorization, dense II.65
Fibrant arrow IV.168
Fibration of pointed objects IV.184
Fibration, effective discrete, of equivalence relations VIII.368
Fibre (of a map) VIII.402
Fibre (over a point) VIII.401
Fibre-determined category III.146
Filter, complete II.56
Filter, completely prime II.56
Filtering functor VII.352
Finitary localization VI.297
Finitary monad VI.275
Finite element II.89
Finitely extensive category III.115
Finitely presentable object VI.282
Fit locale II.82
Fork IV.178
Fork, exact IV.178
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -closed class of morphisms
-closed class of morphisms 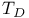 -space
-space 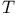 -algebra
-algebra  -biquotient map
-biquotient map 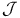 -closed arrow
-closed arrow 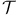 -Models, category of
-Models, category of  -set
-set