|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| McComb W. D. — The Physics of Fluid Turbulence |
|
|
 |
| Предметный указатель |
Quasi-particle approach 141 143
Quasi-stationarity, of decaying turbulence 314—325
Quian, J. 294
Rabie, L.H. 134 470 506 508 509 510 511 519 520
Radin, I. 140 521
Raithby, G.D. 125
Rajagopalan, S. 62 410 425
Ramaprian, B.R. 24 31 33
Ramond, P. 378
Ramu, K.L.V. 519
Rao, P.V. 133 419
Rapaport, D.C. 402
Rate of strain tensor 496
Reduced probability distribution functions 158
Reduced probability distribution functions, distribution vector 159
Reece, G.J. 128
Reed, J.C. 498
Reeks, M.W. 483
Reichl, L.E. 3 163 165 182 205 206 240 361
Reid, W.H. 78 433
Reischman, M.M. 501 505 506 507 508 515
Relative diffusion 449—452
Relative diffusion, extension to three dimensions 452
Relative diffusion, Richardson's law 451
Renormalization 141 143
Renormalization group (RG) 148—149
Renormalization group (RG), and upper critical dimension 349
Renormalization group (RG), application to randomly stirred fluid motion 350—351
Renormalization group (RG), application to sub-grid-scale modelling of turbulence 351—353
Renormalization group (RG), applied to critical phenomena 346
Renormalization group (RG), epsilon expansion 349
Renormalization group (RG), fixed point 148 348
Renormalization group (RG), Forster-Nelson-Stephen theory calculation of the effective viscosity 357—359
Renormalization group (RG), Forster-Nelson-Stephen theory calculation of the effective viscosity, crossover value of e 362
Renormalization group (RG), Forster-Nelson-Stephen theory calculation of the effective viscosity, recursion relations 359—361
Renormalization group (RG), iterative averaging 364
Renormalization group (RG), iterative averaging, conditional (partial) average 367
Renormalization group (RG), iterative averaging, effective dissipation wavenumber 367
Renormalization group (RG), iterative averaging, equations for effective viscosity 377
Renormalization group (RG), iterative averaging, fixed point 377
Renormalization group (RG), iterative averaging, global averaging 368
Renormalization group (RG), iterative averaging, Markovian approximation 375
Renormalization group (RG), iterative averaging, mean field approximation 372 373
Renormalization group (RG), perturbation expansion of the Navier-Stokes equation 355—357
Renormalization, effect on growth of number of terms in perturbation series 339
Renormalization, effective mass of conduction electrons 143
Renormalization, line renormalization 222
Renormalization, partial summation 188—189
Renormalization, screened potential 143 202—203
Renormalization, vertex renormalization 222
Renormalized perturbation theory 144
Renormalized perturbation theory and the turbulence closure problem 184
Renormalized perturbation theory, application to Navier-Stokes equation 205—212
Renormalized perturbation theory, direct-interaction approximation DIA 144
Renormalized perturbation theory, equilibrium system with weak interactions 190—205
Renormalized perturbation theory, perturbation series 146
Renormalized perturbation theory, primitive expansion 208—212
Renormalized perturbation theory, renormalized perturbation series 147
Reshotko, E. 498
Resistance to flow see “Wall shear stress”
Reversion of power series 240—241 289
Reynolds averaging 7 40
Reynolds equation (for the mean velocity in duct flows) 19
Reynolds number, based on Taylor Microscale (Taylor-Reynolds number) 82
Reynolds number, for boundary layer on a flat plate 12
Reynolds number, for decaying turbulence 31—32
Reynolds number, for dissipation range of wavenumbers 69
Reynolds number, for non-Newtonian fluids 498
Reynolds number, for pipe flow 4
Reynolds stress 8
Reynolds stress, closure approximation 336
Reynolds stress, experimental distribution in duct flows 28
Reynolds stress, experimental distribution in duct flows, in a free jet 32
Reynolds stress, governing equation 10
Reynolds stress, total shear stress tensor 8
Reynolds's analogy 464
Reynolds, O. 4 6 7 8 24 82 110
Reynolds, W.C. 387 388 417 419
Richardson's law see “Relative diffusion”
Richardson, L.F. 451
Riley, J.J. 386 397 414 416 428 432 448 456
Rivet, J-P. 403
Roach, G.F. 37
Roache, P.J. 112
Roberts, P.H. 452 479
Robertson, H.P. 49 50 59
Rodi, W. 127 128
Rogallo, R.S. 117 124 386 397
Rogers, M.M. 426
Rollin, A. 500
Ronis, D. 379
Rose, H.A. 223 290 352 353
Rosen, G. 176
Roshko, A. 109 407 408 409 432
Ross, M.A.S. 416
Rudd, M.J. 98 505 506
Ruiz de Elvira, A. 337
Runstadler, P.W. 110 417
Ryskin, G. 126
Sabersky, R.H. 519
Sabot, J. 420 424
Saffman, P.G. 105 338 401 427 428 446 447
Sagdeer, R.Z. 142
Sahlin, A. 498
Saibel, E. 502 503
Salih, S.M. 471 490
Salpeter, E.E. 205
Sampanthar, S. 185
Sandborn, V.A. 103
Sano, Y. 506
Satyaprakash, B.R. 109 329
SBLHDI, SBALHDI see “Lagrangian-history direct-interaction theories”
Scalar transport in homogeneous turbulence 471
Scalar transport in homogeneous turbulence, application of RPTs 478—479
Scalar transport in homogeneous turbulence, Batchelor wavenumber 475
Scalar transport in homogeneous turbulence, Batchelor's model for the viscous ranges of wavenumbers 477—478
Scalar transport in homogeneous turbulence, diffusion cut-off wavenumber 474
Scalar transport in homogeneous turbulence, inertial-convective range of wavenumbers 474
Scalar transport in homogeneous turbulence, inertial-diffusive range of wavenumbers 475
Scalar transport in homogeneous turbulence, numerical simulation 479
Scalar transport in homogeneous turbulence, scalar transfer spectrum 473
Scalar transport in homogeneous turbulence, spectral covariance 472
Scalar transport in homogeneous turbulence, spectrum of scalar variance 473
Scalar transport in homogeneous turbulence, summary of spectral forms 478
Scharf, R. 512
Schertzer, D. 328
Scheuerer, G. 128
Schlicting, H. 8 12 20 33
Schlien, D.J. 448 449
Schmidt number see also “Heat and mass transfer”
Schmidt number, eddy (turbulent) form 464
Schmidt number, molecular form 462
Schnedler, E. 351
Schraub, F.A. 110 417
Schumann, U. 124 334 335 383 387
Schwar, M.J.R. 490
Schwarz, W.H. 496
Self-consistent field (SCF) theory 257—265
Self-consistent field (SCF) theory, comparison with EFP theory 262
Self-consistent field (SCF) theory, Liouville equation 258
Self-consistent field (SCF) theory, perturbation expansion 261
Self-consistent field (SCF) theory, self-consistency criterion 260
Self-consistent field (SCF) theory, single-mode distribution 259
Self-consistent field (SCF) theory, single-mode operator 259
Self-consistent field (SCF) theory, theory of Balescu and Senatorski 264
Self-consistent field (SCF) theory, theory of Phythian 264—265
Self-consistent field (SCF) theory, time-dependent Liouville equation 262
Senatorski, A. 225 264
Serra, R. 429
Seshadri, V. 141 513
| Seyer, F.A. 500
Shanmugasundaram, V. 311 313 316 319 320 324 327 342 352 353 398 401
Shannon, C.E. 291
Sharma, R.S. 141 513 514
Shaver, R.G. 498 499 500 509
She, C.Y. 490
Sheih, C.M. 106
Shenoy, A.V. 499
Shin, H. 135
Shirazi, M.A. 490
Shore, J.E. 291
Sidahmed, G.H. 518
Siggia, E.D. 223 290 383 384 402 427
Simpson, R.L. 419
Skewness of probability distribution 530
Skewness of probability distribution, for decaying turbulence 314
Skewness of probability distribution, independence of Reynolds number 384
Skewness of probability distribution, of the longitudinal velocity difference 102
Skewness of probability distribution, theoretical predictions of 319
Smagorinsky model see “Subgrid models”
Smagorinsky, J. 120 122 123
Smith, D.M. 95
Smith, K.A. 135 138 139 507
Snyder, W.H. 448 456 490
Sokolov, M. 414 415
Spalart, P.R. 386 427
Spalding, D.B. 125 130
Spangler, J.G. 510
Speziale, C.G 128 389
Spiegel, E.A. 429
Sreenivasan, K.R. 410 425
Stationary turbulence 53
Stationary turbulence, under the action of external stirring forces 71—72
Statistical formulation, many-point form 39—42
Statistical formulation, many-time moments in wavenumber space 63—64
Statistical formulation, single-point form 7—11
Statistical formulation, single-time moments in wavenumber space 64—65
Stegen, G.R. 84 106
Steiner, T.R. 410
Stephen, M.J. 350 357
Stewart, R.W. 104 107 117 269 321 325
Stewart, W.E. 461
Stone, E. 428
Strickland, J.H. 419
Structural turbulence see “Non-Newtonian flows”
Structure functions 102 328
Sub-ensemble Eulerian correlation coefficient 447
Subgrid models see also “Large-eddy simulation eddy
Subgrid models, application of RG 397—399
Subgrid models, application of RPT 391—397
Subgrid models, assessment of subgrid models 388—389
Subgrid models, Smagorinsky model 122
Sulem, P-L. 107
Sumer, B.M. 490
Suraiya, T. 518
Swanson, W.M. 515
Takeuchi, K. 377
Talathi, M.M. 499
Tanner, R.I. 502 503 521
Tatsumi, T. 78
Tavoularis, S. 409
Taylor hypothesis of 'frozen convection' 62
Taylor microscale 51—52
Taylor microscale, for decaying turbulence 313—324
Taylor's analysis of turbulent diffusion see “Diffusion by continuous movements and relative diffusion”
Taylor, A.R. 519 520
Taylor, G.I. 36 62 73 75 82 400 437 441 445 448 453 467 483 486
Taylor, T.D. 112
Taylor, W.D. 138
Taylor-Green vortex 400
Taylor-Reynolds number see “Reynolds number”
Tchen's analysis see “Diffusion by continuous movements”
Teh, E.W. 414
Tels, M. 511
Temam, R. 330
Tennekes, H. 83 84 86 103 105 106 330
TerHaar, D. 143
Test problems in isotropic turbulence 176—181
Test problems in isotropic turbulence, free decay 177
Test problems in isotropic turbulence, stationary turbulence 179
Test problems in isotropic turbulence, stationary turbulence, cross-correlation of stirring force with the velocity field 181
Test problems in isotropic turbulence, stationary turbulence, random stirring forces 180
Test-field model see “Near-Markovian model closures”
Thin shear layer see “Boundary layer approximation”
Thomas, A.S.W. 431
Thomas, D.M.C. 445
Thompson, D.W. 509
Thwaites, B. 33
Tiederman, W.G. 419 505 506 507 508 510 515
Time scales see “Eddy turnover time” “Integral “Lagrangian “Lagrangian “Taylor
Time series analysis 98
Time series analysis, aliasing errors 99
Tollmien-Schlicting waves 430
Tolmien, W. 24 31
Toms, B.A. 132
Townsend, A.A. 33 75 86 100 103 105 321 410 475 484
Transfer spectrum see “Energy transfer spectrum” “Scalar
Transition from laminar to turbulent flows 406
Transitional structures see “Coherent structures”
Transport power 236 296
Transport power, for decaying turbulence 313
Troutt, T.R. 409
Tsinober, A. 351
Tsuji, Y. 490
Tu, B.J. 421
Tukey, J.W. 99
Tulin, M.P. 519
Tullis, J.P. 519
Tur, A.V. 142
Turbulence models, 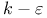 model 128 model 128
Turbulence models, algebraic stress models 128
Turbulence models, two-equation models 127
Turbulent bursts 110—122
Turbulent bursts, ejection-sweep cycle 112 417
Turbulent bursts, frequency of bursts 418—420
Turbulent bursts, frequency of bursts in drag-reducing fluids 509—521
Turbulent bursts, low-speed streaks 110—417
Turbulent bursts, production of turbulence 111
Turbulent bursts, streaky structure 418
Turbulent bursts, streaky structure and streamwise vortices 420—423
Turbulent diffusion in an Eulerian frame see “Diffusion by continuous movements” “Heat “Scalar
Turbulent diffusion of particles (in an Eulerian framework) see also “Diffusion by continuous movements”
Turbulent diffusion of particles (in an Eulerian framework), finite-step diffusion coefficient 486
Turbulent diffusion of particles (in an Eulerian framework), governing equation 480—482
Turbulent diffusion of particles (in an Eulerian framework), mean motion effects 483 490
Turbulent diffusion of particles (in an Eulerian framework), measurements in turbulent flows 489—490
Turbulent diffusion of particles (in an Eulerian framework), perturbation treatment of finite inertia 488—489
Turbulent diffusion of particles (in an Eulerian framework), random walk models 484—487
Turbulent diffusion of particles (in an Eulerian framework), turbulent diffusion coefficient 481—483
Turbulent mixing 490—491
Turbulent mixing, diffusion limited 491
Turbulent spots see “Coherent structures”
Two-dimensional mean flows 1
Two-dimensional mean flows as a special case 12
Uberoi, M.S. 84
Ueda, H. 424
Ultraviolet catastrophe 166
Umhauer, H. 490
Unidirectional laminar flow 3
Unphysical oscillations, in response function of DIA 317
Unphysical oscillations, in response function of LET 324
Usui, H. 505 506 508 509 511 518
Van Atta, C.W. 78 84 106 107 165 313 329 416
van Beijeren, H. 190
Van Der Hegge Zijnen, B.G. 470 471 487
Van Doormaal, J.P. 125
van Driest, E.R. 388 499 507
Van Dyke, M. 31 34
Vaseleski, R.C. 141 497
Vassiliadou, E. 518
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



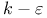 model
model