|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Feller W. Ч Introduction to probability theory and its applications (Volume II) |
|
|
 |
| ѕредметный указатель |
Abel summability 627 628 648
Abelian theorems 418 445
AbelТs integral equation 33
Absolute continuity 139 140
Absolute probabilities 207Ч209
Absolutely fair 210
Absolutely monotone functions 223Ч224 439 441
Absorbing barriers 340Ч342 464 477Ч479
Absorption (physical) 25 31 323
Accidents 57 181
Additive set functions 107
Additive set functions, countably = sigma 108 119 129Ч130
Age see УDurationФ
Algebra of sets 112Ч113 116
Algebra of sets, generation of 163
Ambarzumian, V.A. 206 325
Anomalous numbers 63
Arc sine distributions 50
Arc sine distributions and limit theorems 470Ч473
Arc sine distributions in random walks 417Ч423
Arithmetic distributions 138 407Ч408
Arrays, null 177Ч178 585
arrays, triangular 177Ч178 216 308Ч312 583Ч588 596
Arzela Ч Ascoli theorem 270
Ascending ladder variables, strict 391
Ascending ladder variables, weak 392Ч393
Associated random walks 406
Astronomy, applications to 33 172 173Ч174 206 215 325Ч326
Asymptotic behavior 521 572
Asymptotic estimates 375Ч377 410Ч411
Asymptotic properties of regularly varying functions 279Ч284
Asymptotically dense 147
Asymptotically negligible 178
Asymptotically unbiased estimators 220
Atomic measures 137Ч138
Atoms (of measures) 137
Atoms (of measures), under convolutions 147 149 166
Attraction see УDomain of attractionФ
Auto-regressive process 89 96
Bachelier process see УBrownian motionФ
Backward equations 357
Backward equations for diffusion 334 336Ч337 344
Backward equations for jump processes 327Ч328 484Ч487
Backward equations for semi-groups 352 356Ч357
Backward equations for semi-Markov processes 497
Backward equations of Kolmogorov 327Ч328
Backward equations, minimal solution of 322 329Ч331 486
Bad luck 15Ч17
Baire functions 104Ч106 109 114 130 305 351
Banach space 257 350 487
Barriers see УAbsorbing barriersФ УBoundary УReflecting
Barucha-Reid, A.T. 656
Baxter, G. 404 424 571 605
Bayes, T. 56
Benes, V.E. 379 656
Benford, F. 63
Bergstroem, H. 581
Bernouilli trials 1 141Ч142
Bernstein polynomials 222Ч223
Bernstein polynomials in 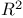 245 245
Bernstein, S. 79 439
Berry Ч Esseen theorems 538 542Ч546 551
Berry, A.C. 531 536 542
Bessel density 502
Bessel functions 58Ч61 523
Bessel functions and infinite divisibility 177 451 566
Bessel functions and Laplace transforms 437 438 479Ч482
Bessel functions and related distributions 58Ч61 149 166
Bessel functions in stochastic processes 58Ч61 323
Bessel functions, characteristic function of 503
Beta density 50
Beta density in renewal 471
Beta integral 47
Bickel, P.J. 388
Bilateral exponential 49Ч50 502
Bilateral exponential, characteristic function of 503
Bilateral Laplace transform 434
Billingsley, P. 39 265 343
Binary orbits 33
Binomial random walks 608Ч609
Birth processes 41 266Ч267 488Ч491
Birth processes, bilaterial 491
Birth-and-death processes 479Ч483 496
Birth-and-death processes and diffusion 496
Birth-and-death processes, busy periods in 482Ч483
Bivariate normal density 70
Bizley, M.T.L. 420
Blackwell, D. 360 381
Blum, J.R. 287
Bochner integral 455
Bochner, S. 321 347 454 620 622 634 655
Bohl 268
Borel algebra 113 119
Borel algebra, measurable functions 116
Borel set 114 116 117 123 125 130
Borel set, approximation of 115 124
Borel set, convention for 127
Borel Ч Cantelli 105 317
Botts, T.A. 103
Boudreau, P.E. 196
boundary conditions 337Ч343 477
Bourbaki, N. 103
Branching processes 244 441 474Ч475
Brelot, M. 2.44
Brownian motion 99 181 322Ч349 475Ч479
Brownian motion in 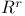 175 344 175 344
Brownian motion, continuity of paths in 181 332
Brownian motion, first-passage times in 174Ч175 340 476
Brownian motion, one absorbing barrier 340 477
Brownian motion, subordination of Cauchy process to 348
Brownian motion, two absorbing barriers 341 478
Brownian motion, with elastic force 335
Buehlmann, H. 229
BuffonТs needle problem 61Ч62
buses 22 55 188
Busy periods 194Ч195 198Ч200 473Ч474 482Ч483
CampbellТs theorem 179 287 595
Canonical measures 560Ч565
Cantelli see УBorel Ч CantelliФ
Cantor distribution 35Ч36 141 593
Cantor distribution, convolutions of 146
Cantor, G. 267
CantorТs diagonal method 267Ч268
Cap and cup 104
Carleman, T. 227 515
Cauchy distribution 50 64 173 502
Cauchy distribution and random walks 204 618
Cauchy distribution and stability 173 555
Cauchy distribution in 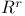 70Ч71 73 100 524 594 70Ч71 73 100 524 594
Cauchy distribution in Brownian motion 175 348
Cauchy distribution, bivariate 524
Cauchy semi-groups 303
Cauchy, A. 172 509
Centering 45 137 584Ч588
Centering in infinitely divisible distributions 559
Central limit theorem 258Ч265 287 291 529Ч530
Central limit theorem and large deviations 548Ч553
Central limit theorem for densities 533Ч536
Central limit theorem for equal components 515Ч518
Central limit theorem in renewal 372
Central limit theorem, applications of 209 529Ч530
Central limit theorem, expansions related to 531Ч553
Central limit theorem, with infinite variances 260
Cesaro summability 628 648
Chains, random 206Ч207
Chains, strength of 9
Chandrasekhar, S. 32
Chapman Ч Kolmogorov equations 60 334 338 346Ч347 353 566
Chapman Ч Kolmogorov equations and semi-groups 351
Chapman Ч Kolmogorov equations, continuous time 322 486Ч488
| Chapman Ч Kolmogorov equations, discrete time 98
Chapman Ч Kolmogorov identity 98
Characteristic exponents of R 170
Characteristic functions 498Ч526 (see also УPoisson summationФ)
Characteristic functions in Rr 521Ч524
Characteristic functions, derivatives of 565Ч566
Characteristic functions, factorization of 506 593 631
Characteristic functions, finitely divisible 557
Characteristic functions, infinitely divisible 554Ч557 560Ч564
Characteristic functions, logarithms and roots of 554Ч555
Characteristic functions, periodic 511 626 630 631
Characteristic functions, Taylor development of 514Ч515
Chebyshev Ч Hermite polynomials 533
ChebyshevТs inequality 151Ч152 310 354
ChebyshevТs inequality for martingales 246
ChebyshevТs inequality, generalized 234
Checkerboard partitions 133
Chernoff, H. 287
Chi-square density 48
Choquet, G. 382 593
Chow, Y.S. 360
Chung, K.L. 105 167 231 355 381 483 614 615 655
Circles, covering theorem for 28Ч29
Circles, densities on 632Ч633
Circles, distributions on 29 61Ч64 627
Circles, equidistribution on 268 273
Circles, probability distribution on 274
Coin-tossing 210 211Ч212 405 417
Coin-tossing and random choice 35
Coincidences 217
Collisions of particles 206 322Ч323 325
Compactness of triangular arrays 309
Complete monotonicity 224Ч227 439Ч442 450 464
Complete monotonicity, abstract 454
Completion of measures 126
Composition of kernels 206
Compound Poisson processes 180Ч181 305 326
Compound Poisson processes and ruin problems 182Ч184 198 469Ч470
Compound Poisson processes and semi-groups 295 299Ч300
Compound Poisson processes and subordination 348Ч349
Concave functions 153
Concentration 4 45 137
Concordant functions 210Ч211 244
Conditional distributions and expectations 71Ч74 156Ч159 160Ч165
Conditional probability 157
Contagion 57Ч58
Continuity of semi-groups 353 (see also УFixed discontinuitiesФ)
Continuity theorem 431Ч433 508
Continuity theorem and Laplace transforms 433
Continuity theorem and quasi-characteristic functions of 557
Continuity theorem and semi-groups 460
Continuity theorem for densities 510
Continuity theorem, characteristic function of 508Ч509 510
Contractions 350 456
Convergence in norm = strong 257 352
Convergence in probability 253Ч254
Convergence in the mean square 636
Convergence of densities 252
Convergence of measures 247Ч252 267Ч270 284Ч285
Convergence of moments 251Ч252 269
Convergence of operators 257 285 352
Convergence, dominated 111
Convergence, notations and principles of 248Ч251
Convex functions 153Ч155
Convex functions of martingales 214Ч215
convex polygons 505
Convolution semi-groups 293Ч296
Convolutions 143Ч148 272 278
Convolutions and covering theorems 26Ч29
Convolutions and Laplace transforms 434Ч435
Convolutions of densities 7Ч8 46 71
Convolutions of singular distributions 146
Convolutions on circles 64 143 273Ч274
Convolutions, definition of 7 8
Convolutions, infinite 265Ч267 317 592Ч593
Coordinate variables 4 68
Correlation 68
Countably many intervals 108
Counters for particles 372 (see also УGeiger countersФ УQueuesФ)
Covariance 68
Covariance of processes 88Ч94 623Ч626 643Ч646
Covariance, matrix 82Ч83
Covering theorems 76 216 469
Covering theorems and convolutions 26Ч29
Cramer Ч Levy theorem 525
Cramer, H. 182 403 522 531 542 546 548 552 646 656
CramerТs estimate for ruin 182 377Ч378 403 411Ч412
Cup 104
Dams 195
Darling, D.A. 465
de Finetti, B. 179 230
decision functions 213
Decompositions 570Ч571
Defective distributions 115 129 130 205
Defective distributions in renewal 187
Degenerate distributions 83 87
Degenerate processes 90Ч91
Delayed renewal processes 187 368
Delays in traffic 190 380 387 474Ч475 496
densities 3Ч6 49Ч53 66Ч71 138Ч143
Densities, notations and conventions for 45Ч46
Denumberable sample spaces 331Ч332
Deny, J. 382
Derivatives and Laplace transforms 435
Derman, C. 493
Descending ladder variables 393Ч394
Differences, notation for 221Ч222
Differential equations, Kolmogorov 483Ч488
Diffusion processes and birth-and-death processes 496
Diffusion processes in 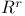 332Ч337 344Ч345 436 461 464 475Ч479 496 332Ч337 344Ч345 436 461 464 475Ч479 496
Diffusion processes in genetics 336Ч337
Diffusion processes in higher dimensions 344Ч345
Diffusion processes, with elastic force 335Ч336
Digits, distribution of 34 63Ч64
Directing process 347
Directional changes of particles 323
Directions, random 29Ч33
Directly Riemann integrable functions 362Ч363
Dirichlet integral 511
Discontinuities 318
Discontinuous semi-groups 305
Discrepancies see УEmpirical distributionsФ
Discrete distributions 55Ч58
Distance function for distributions 285
Distribution functions, definition of 3
Doblin, W. 173 592
DoblinТs УUniversal lawsФ 590Ч592
Domain of attraction 172
Domain of attraction and stable distributions 574Ч581
Domain of attraction, criteria for 312Ч316 320 448 574Ч581
Domain of attraction, normal 581
Domain of attraction, partial 320 568 590Ч592
Dominated convergence 111
Donsker, M.F. 39 343
Doob, J.L. 103 164 210 244 656
Drift in diffusion 335
Drift in random walks 397 610Ч611
Duality 394Ч398 609Ч610
Duplication formula 64
Duration of birth processes 490
Duration of busy period 473Ч474 482Ч483
Duration of dead period 190
Duration of diffusion 341Ч342
Duration of renewal process 187 216 374Ч377
Duration, estimates for 377
Dvoretzky, A. 274
Dynkin, E.B. 321 333 472 655
Economics, stable distributions in 175
Edgeworth expansion 535 542
Einstein, Albert Jr. 182 333
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте