|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Feller W. Ч Introduction to probability theory and its applications (Volume II) |
|
|
 |
| ѕредметный указатель |
Elastic forces 335Ч336
Electric transmission lines 208Ч209
Empirical distributions 36Ч39
Empirical interpretations 22
Endomorphisms 350
Energy losses 25 323
Ensembles of circles and spheres 9Ч10
Ensembles, random, of points in space 9
Entrance probability see УHitting pointsФ
Equicontinuity 252 270
Equidistribution theorem 268
Equivalent functions 125 636 642
Erdoes, P. 343 360
Ergodic limits 491Ч493
Ergodic stochastic kernels 271
Ergodic theorems 270Ч274 491
Esscher, F. 552
Esseen, G. 540 542 544 545
Estimator 41
Exchangeable variables 228Ч230 423
Exchangeable variables, central limit theorem for 287
Expansions and the central limit theorem 531Ч553
Expansions for distributions 538Ч542
Expansions, involving varying components 546Ч548
Expectations 117Ч118 133
Expectations, conditional 162Ч165
Expectations, definition of 5
Explicit expressions 193
Exponential distributions 1 8Ч21 39Ч43 74Ч77
Exponential distributions and uniform distributions 44 74Ч77
Exponential distributions as limits 24 43 370
Exponential distributions, bilateral 49 148
Exponential distributions, bivariate 100
Exponential distributions, reduction to 25Ч26
Exponential formula of semi-groups 231 353Ч355
Extension theorem 118Ч121 123
Fair, absolutely 210
FatouТs theorem 110Ч111 636
FatouТs theorem for boundary values 244
Fejer, L. 628
Feller, W. 53 61 179 194 262 279 289 325 331 333 337 360 381 430 483 496 497 546 552 581
Filters 88 625
Finetti, B. de 42 179 230
Finite arithmetic distributions 608Ч609
First entry see УHitting pointsФ УLadder
First passages and Markov chains 492
First passages in diffusion 174Ч175 340Ч341 475Ч476
First passages, birth-and-death processes 60Ч61 481 494Ч495
First return 391 424 495
Fisher, R.A. 77 277 336
FisherТs Z-statistic 49
fishing 182
Fixed discontinuities 324Ч326 328
Fokker Ч Planck equation 296 323 324 325 328
Forward equations 337Ч343 484
Forward equations and diffusion 337Ч343 475Ч479
Forward equations and jump processes 324 .328
Forward equations and semi-groups 352
Forward equations of Kolmogorov 324 328
Forward equations, minimal solution for 329 331Ч332 485Ч488
Fourier analysis, applications of to random walks 598Ч616
Fourier coefficients 628 634 647Ч648
Fourier inversions 509Ч510 511 639
Fourier series 626Ч629 641
Fourier transforms 499 532
Fourier Ч Stieltjes transform 499 606
fractional parts 148 268
FrechetТs maximal distribution 166
Free paths 10Ч11
Frequency functions, definition of 8
FubiniТs Theorem 111 122 144
Fuchs, W.H.J. 614 615
Functional, linear 120
Galton, F. 73
Gamma distributions 11 47Ч48 176 435 502 503
Gamma distributions, alternate name for 48
Gamma distributions, approximation by 220
Gamma distributions, infinitely divisible 176 451 567
Gamma distributions, limit of order statistics 24
Gamma distributions, randomized 58Ч59
Gamma distributions, subordination 336Ч337
Gamma functions 47
Gamma process, direction of by Poisson process 349
Gamma process, direction of by Poisson process, direction of Poisson process by 348Ч349
Gaps, large 188 378 468
Gaps, small 217
Geary, R.C. 86
Geiger counters 189 190 372Ч373 387 468
Generating functions, characterization of 223
Generating functions, mortality interpretation for 424
Generation of algebras 163
Generation of exponentially distributed variables 44
Generators 294Ч296 356Ч357 456Ч457 476
Genetics, diffusion in 336Ч337
Gilbert, E.N. 217
Gnedenko Ч Koroljuk theorem 43
Gnedenko, B.V. 38 39 277 531 540 581 592 656
Good, I.J. 473
Gravitational fields 173Ч174 215
Green function 334 476 496
Greenwood, M. 57
Grenander, U. 77 655 656
Griffin, J.S., Jr. 196
Grouping of data 4Ч5
Growth, logistic 52
Gumbel, E.J. 165
HadamardТs factorization theorem 525
Halmos, P.R. 103 213
Hamel equation 298 305
Hardy, G.H. 155 268 445
Harmonic analysis 619Ч646
Harmonic functions 244
Harris, T.E. 244
Hausdorff, F. 226
Height distribution 73
Heitler, W. 323
Helly, E. 267
Hennequin, E. 103
Herglotz, G. 634
Hermite polynomials 523Ч533 535
Hermite polynomials, expansion of 542
Hewitt, E. 124 229
Heyde, C.C. 227
Hidden periodicities 76
Hilbert spaces 271 637 639Ч643 645
Hille Ч Yosida theorem 458Ч463 476
Hille, E. 231 294 408 454 525 656
Hitting points see УLadder variablesФ
Hitting points in random walks 426 598Ч599
Hitting points in renewal 188 371Ч372 426
Hobby, C. 389
HolderТs Inequality 155
Holtsmark distribution 172 173Ч174 215
Hopf, E. 403 (see also УWiener Ч HopfФ)
Hunt, G. 210
HuygensТ principle 51
Hyperbolic functions and densities 502Ч503 527 567 632Ч633
Ibragimov, I.A. 167
Idle servers 200
Images, method of 340
Imbedded renewal processes 191Ч193 379
Improper see УProper distributionsФ
Increase, point of 137 147
Independence of random variables 6 69 71 121Ч125 134
Independence of random variables and complex variables 498
Independence of random variables, criterion for 136
Independent increments 95Ч96 179Ч182 293 304 317 645
Independent increments and discontinuities 305 317Ч318
Independent increments and subordination 347
Index of the first maximum 417
| Indicators 104
Induced partitions 22
Induced random walks 390
Inequalities 152Ч156
Inequalities of Hoelder 155
Inequalities of Jensen 153Ч154
Inequalities of Kolmogorov 156
Inequalities of Schwarz 152Ч153
Inequalities, moment 155
Infinite convolutions 265Ч267 317 592Ч593
Infinite differentiability 256 293
Infinitely divisible distributions 176Ч179 292Ч293 449Ч452 554Ч595
Infinitely divisible distributions and semi-groups 290Ч318 457Ч458
Infinitely divisible distributions in 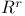 593 596 593 596
Infinitely divisible distributions, special properties of 570Ч574
Infinitesimal generators 456
Infinitesimal speed and variance 335
Inner products 636
Inspection paradox 187 372
Insurance see УRisk theoryФ
Integrals, stochastic 645Ч646
Integration by parts 150Ч151
Integration by parts and Laplace transforms 435Ч436
Interval functions 106Ч112 128 129
Interval of continuity 248
Invariance principle 343
inventories 195Ч196
Inversion formulas 140 221Ч222 638
Inversion formulas and moment problems 227
Inversion formulas for Laplace transforms 232Ч234 440Ч441 462
Inversion formulas, characteristic functions for 510Ч511 524
Ionization 323
Isometry 638
Ito, K. 333 655
JacobiТs theta functions 342 345 632
Janossy, L. 323
JensenТs Inequality 153Ч154 214
Joint distributions 68 423Ч425
Jordan decomposition 138 142
Joseph, A.W. 420
Jump processes 326Ч332
Jump processes, with infinitely many jumps 331 484
Kac, M. 79 196 343
Karamata, J. 173 247 275 279 445
Karlin, S. 228 381 656
Katz, M.L. 545
Kelvin; Lord 340
Kemperman, J.H.B. 655
Kendall, D.G. 194 231 473
Kernels, stochastic 159 205 270Ч272
Khintchine A. 137 173 179 406 527 565 588 592 639Ч640 656
Khintchine Ч Pollaczek formula 410 470 617
KhintchineТs criterion 639Ч640
KhintchineТs law of large numbers 235 436
KhintchineТs unimodality criterion 158 527
Kiefer, J. 200
Kingman, J.F.C. 184
Kolmogorov Ч Smirnov theorem 39 342Ч343
Kolmogorov, A.N. 39 123 124 179 325 333 531 540 656
KolmogorovТs backward equation 327 328
KolmogorovТs differential equations 331 483Ч488
KolmogorovТs forward equation 324 328
KolmogorovТs inequality 156 246
KolmogorovТs inequality for martingales 242
KolmogorovТs inequality for positive submartingales 241Ч242
KolmogorovТs three-series theorem 317
Koroljuk, V.S. 33 38 39 43
Krickeberg, K. 103 655
Kronecker delta kernel 206 484
KroneckerТs lemma 239 243
Ladder epochs, distribution of 413Ч417
Ladder heights 191 398Ч400
Ladder indices 412Ч413
Ladder points 390
Ladder variables, ascending, strict 391
Ladder variables, ascending, weak 392Ч393
Ladder variables, descending 393Ч394
Laha, R.G. 655
Lamperti, A. 189
Landau, E. 342 446
Landau, L. 323
Laplace transforms 232Ч233 429Ч458
Laplace transforms and convolutions 434Ч435
Laplace transforms and derivatives 435
Laplace transforms and integration by parts 435Ч436
Laplace transforms and moments 435
Laplace transforms and random walks 614
Laplace transforms for semi-groups 454Ч458
Laplace transforms in 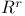 452Ч454 452Ч454
Laplace transforms, applications of 466Ч495
Laplace transforms, elementary properties of 434Ч436
Laplace transforms, examples of 436Ч439
Laplace transforms, inversion formulas for 232Ч234
Laplace Ч Stieltjes transform 432 470 495 496
LaplaceТs second law 50
Last come first served 190
Lattice distributions 138 (see also УPoissonТs summation formulaФ)
Lattice distributions, central limit theorem for 517Ч518 540
Lattice distributions, characteristic functions for 511
Lattices (algebraic) 350
Law of Large Numbers 219Ч246 286 436 513
Law of large numbers for identically distributed variables 234Ч237
Law of large numbers for stationary sequences 245
Law of large numbers for triangular arrays 316Ч317 596
Law of large numbers, converse 241
Law of large numbers, KhintchineТs law 235
Law of large numbers, strong law 237Ч241
Law of large numbers, weak law 235Ч236
Le Cam, L. 286
Lebesque completion 126
Lebesque decomposition theorem 142
Lebesque measure 33Ч36 126
Lebesque Ч Nikodym theorem 140 (see also УRiemann Ч Lebesque theoremФ)
Lebesque Ч Stieltjes integral 110 119 121 131Ч132
Leffler see УMittag Ч LefflerФ
LegendreТs duplication formula 64
Length of random chains 206Ч207
Levy Ч Pareto distribution 172 (see also УPareto distributionФ)
Levy, P. 173 179 181 210 262 274 285 305 314 318 497 515 525 565 567Ч568 571 575 588 592 655 656
LevyТs canonical measure 564
LevyТs examples 215 319 567Ч568
LevyТs metric 285
Lifetime see УDurationФ УRecurrence
Light in stellar systems 206 325Ч326
Light, absorption of 31
Light, HuygensТ principle of 51
Light, intensity of 25
Light, transmission of through matter 25 31 43
Likelihood ratios 211
Limit theorems 24 342Ч343
Limit theorems and arc sine distributions 470Ч473
Limit theorems and queues 380
Limit theorems, basic 247Ч288
Lindeberg conditions 262 263 286 518Ч521 530
Lindeberg conditions in diffusion 333
Lindeberg.J.W. 515
Lindley, D.V. 194 389
Linear functional 120
Linear increments in jump processes 324Ч326
Linear operators on stochastic processes 625Ч626
Little, J.D.C. 474
Littlewood, J.E. 155 445
LjapunovТs condition 286
Locally compact spaces 120 123 248
Locked period 189
Loeve, M. 103 104 229 .265 321 655
Logarithmic distribution 63
Logistic distribution and growth 52Ч53
Lost calls 190 495.
Luck, persistence of 15Ч17
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте