|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Feller W. Ч Introduction to probability theory and its applications (Volume II) |
|
|
 |
| ѕредметный указатель |
Lukacs, E. 86 655
Lundberg, F. 182
Mandelbrot, B. 175 288
Marginal distribution 67 134 157
Marginal distribution, normal 100
Marginal distribution, prescribed 165
Markov processes with continuous time 96 321Ч345 624Ч625 УSemi-Markov
Markov processes with continuous time and ergodic theorems 369 491Ч492
Markov processes with continuous time and semi-groups 349Ч357 454Ч458
Markov processes with continuous time in countable spaces 483Ч488
Markov processes with discrete time 94Ч99 101Ч102 205Ч209 217
Markov processes with discrete time and ergodic theorems 270Ч274
Markov processes with discrete time and martingales 244
Markov processes with discrete time and spectral aspects 635 649
Markov property 8Ч9
Markov property, strong 20
Markov, A. 228
Marshall, A.W. 246
Martingales 209Ч215 241Ч244
Martingales, inequalities for 241Ч242 246
Matrix calculus 82Ч83 484Ч485
Maximal partial sums 198 402 408Ч412 419Ч423
Maximal partial sums, estimate of 412
Maximal recurrence time 189 386
Maximal row sums 320 597
Maximal term 172 277 287 465 УRecord
Maxwell distribution 32 48 78Ч79
Mc Kean, H.P.Jr. 333 655
Mc Shane, E.J. 103
Mean approximation theorem 111Ч112
Mean square convergence 636
Mean value theorem 109
Measurability 113Ч115
Measure space 115
Median 17 137
Metrics for distributions 285 (see also УBanach spaceФ УHilbert
Microscopes 31
Middleton, D. 631
Milky Way brightness 325
Miller, H.D. 603
Mills, H.D. 101
Minimal solutions and diffusions 339
Minimal solutions and jump process 329Ч331
Minimal solutions and semi-Markov processes 497
Minimal solutions and W1Ener Ч Hopf equation 402
Minimal solutions of Kolmogorov differential equations 485Ч488
Mirror experiment 51
Mittag Ч Leffler function 453Ч454
Mixtures 53Ч55 73 159 167
Mixtures and transforms 437 504
Moments 5 136 151 570
Moments and derivatives 435
Moments in renewal 375
Moments, convergence of 251Ч252 269
Moments, generating function 434
Moments, Hausdorff moment problems 224Ч228 245
Moments, inequalities 155
Moments, uniqueness problem 227 233 514Ч515
Moments, uniqueness problem, in 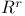 529 529
Monotone convergence principle 110
Monotone convergence principle, property of 350Ч352
Monotone functions 275Ч277
Monotone sequences 105
Mortality, random walks with 424
Moving average processes 88Ч89 645
Muentz, H.Ch. 245
Multivariate normal characteristic functions 522Ч523
Natural scale in diffusion 333
nearest neighbors 10
Needle problems, BuffonТs 61Ч62
Nelson, E. 100 347
Neumann, J.V. 44
Neumann, K., identity of 60
Neveu, J. 103 655
Newell, G.F. 40
Neyman, J. 182
Nikodym see УRadon Ч NikodymФ УLebesque
Noise see УShot effectФ
Nonlinear renewals 387
Norm 256 350 636 642
Norm, topology 286
Normal distributions 46 64 87 173 503 566
Normal distributions in 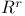 83Ч87 522 83Ч87 522
Normal distributions, bivariate 70 72 101
Normal distributions, characterization of 77Ч80 85 525Ч526
Normal distributions, degenerate 87
Normal distributions, domain of attraction 313 577Ч578
Normal distributions, marginal 99Ч100
Normal distributions, Markovian 94
Normal semi-groups 299 307 319
Normal stochastic processes 87Ч94 641Ч646
Nucleons 323
Null arrays 177Ч178 583Ч588
Null sets 125Ч126 140
Nyquist, N. 631
Operational time 181 345
Operators associated with distributions 254Ч258
Optional stopping 213
Orbits, binary 33
Order relation in 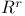 82 132 82 132
Order statistics 18 20Ч21 100
Order statistics and limit theorems 24 43
Order statistics, application to estimations 41
Orey, S. 381
Ornstein Ч Uhlenbeck process 99 335Ч336
Oscillating random walks 204 395
Osipov, L.V. 545
Paradoxes 11Ч14 23 187
Pareto distribution 50 175
Parseval relation 463 507 615 619Ч620 638 641 644
Parseval relation as Khintchine criterion 639Ч640
Partial attraction 320 568 590Ч592
Partial ordering 82 132
Particles, collisions of 206 322Ч323 325
Particles, counters for 372
Particles, directional changes of 323
Particles, energy, losses of 323 325
Particles, splitting of 25 42 100
Patients, scheduling of 183
Pearson, K. 48
PearsonТs system of distributions 48 50
Pedestrians 189 378 387
Periodograms 76
Persistency see УTransient distributionsФ
Petersburg game 236
Petersen, D.P. 631
Petrov, V.V. 545 552
Phillips, R.S. 231 294 454 656
Pinkham, R.S. 63
Pitman, E.J.G. 565
Plancherel theorem 510
Plancherel transform 637Ч640
Planck see УFokker Ч PlanckФ
Platoon formation 40
Poincare, H. 62
PoincareТs roulette problem 62Ч63
Point functions 128
Poisson distributions 566
Poisson distributions, approximations by 286
Poisson distributions, compound 555 557Ч558
Poisson distributions, difference of 149 166 567
Poisson ensembles 15 (see also УGravitational fieldsФ)
Poisson kernel 627 648
Poisson processes 12 14Ч15 УPseudo-Poisson
Poisson processes as limit in renewal 370
Poisson processes, direction of by gamma process 348Ч349
Poisson processes, direction of gamma process by 349
Poisson processes, gaps in 378
Poisson processes, supremum in 183
PoissonТs summation formula 63 343 629Ч633 648
| Polar coordinates 68
Pollaczek, F. 198 (see also УKhintchine Ч PollaczekФ)
Pollak, H.O. 217
Pollard, H. 360 381
Polya distribution 57
PolyaТs criterion 505 509
PolyaТs urn 210 229Ч230 243
Polymers 206
Population growth 337
Population growth, logistic 52Ч53
Population growth, random dispersal of 261Ч262
Port, S.C. 279
Positive definite functions 620Ч623
Positive definite matrices 81
Positive definite sequences 633Ч635
Positive variables 571Ч572
Potentials 488
Power spectrum 624
Prabhu, N.U. 656
probability density see УDensitiesФ
Probability distributions 130
Probability distributions in 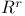 127Ч165 127Ч165
Probability measures and spaces 103Ч116 133
Processes with independent increments 179Ч184
Product measures and spaces 121Ч123
Prohorov, Yu.V. 39 343
Projection 67
Projection of random vectors 30 32 33
Proper convergence 248 285
Proper distributions 130
Pseudo-Poisson processes 322Ч324 345
Pseudo-Poisson processes and exponential formula 354
Pseudo-Poisson processes and semi-groups 354Ч357 459
Pseudo-Poisson processes with linear increments 324Ч325
Pure birth process 488Ч491
Pyke, R. 183 389 470 497
Quasi-stable distributions 173
Queues 54Ч55 65 196Ч197 208 481Ч482
Queues and limit theorems 380
Queues and paradoxes 12Ч14
Queues for shuttle trains 196Ч198
Queues, joint distribution for residual and spent waiting times 386
Queues, one-server 194Ч195
Queues, parallel 17 18 41
Queuing processes 194Ч200 208 380 410
Radiation, stellar 206
Radon Ч Nikodym derivative 139
Radon Ч Nikodym theorem 139 140 141
RaikovТs theorem 571
Random chains 206Ч207
Random choice 2 21Ч25 69
Random choice and coin tossing 35
Random directions 29Ч33 42 43 142
Random directions, addition of 31Ч33 207 523
Random dispersal 261Ч262
Random flights 32Ч33
Random partitions 22Ч23 74Ч75
Random splittings 25Ч26 42 100
Random sums 54 159 167 504
Random sums, central limit theorems for 265 530
Random sums, characteristic function for 504
Random variables 4 68 116Ч118 131
Random variables, complex 499
Random vectors 31 33 107Ч108
Random walks in  190Ч193 200Ч204 389Ч425 598Ч616 УLadder 190Ч193 200Ч204 389Ч425 598Ч616 УLadder
Random walks in  , associated 406 , associated 406
Random walks in  , empirically distributed 38 , empirically distributed 38
Random walks in  , simple ( = Bernouilli) 213Ч214 318 393 395 425 437 , simple ( = Bernouilli) 213Ч214 318 393 395 425 437
Random walks in 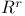 32Ч33 32Ч33
Random walks in 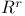 , central limit theorem for 261 , central limit theorem for 261
Randomization 53Ч64
Randomization and exchangeable variables 228
Randomization and semi-groups 231 355
Randomization and subordination 345Ч349
Randomized random walks 58Ч61 479Ч483 566Ч567
Ratios 16Ч17 24Ч25 54
Ray, D. 333
Rayleigh, Lord 32Ч33 523
Record values 15Ч16 40
Rectangular density 21 50
Recurrence time 184
Recurrence time, maximal 189 386
Recurrence time, observed 13 187
Recursive procedures 26
Reflecting barriers 340 343 464
Reflection principle 175 477 478
Regeneration epochs 184
registrations 191 373
Regression 72 86
Regular stochastic kernels 271Ч273
Regular variation 275Ч284 288 289
Reliability theory 52
Renewal epochs 184 372Ч374
Renewal equation 185Ч187 359 366Ч368 385Ч388
Renewal equation, theory of 466Ч468
Renewal processes 12 184Ч187 216 358Ч388
Renewal processes, applications of 377Ч378
Renewal processes, imbedded 191Ч193
Renewal processes, nonlinear 387
Renewal processes, superposition of 370Ч371
Renewal processes, transient 374Ч377
Renewal processes, two-stage 380
Renewal theorems 358Ч372
Renewal theorems on the whole line 201 380Ч385 428
Renewal theorems, proof of 364Ч366
Renyi, A. 343
Reservoirs 182 183 195
Residual waiting time 188
Residual waiting time, limit theorem for 369 370 386 471Ч472
Resolution of identity 643
Resolvents 429 452Ч453 455 487
Resolvents and complete monotonicity 461
Resultant of random vectors 31 146 523
Returns to the origin 424
Richter, W. 552
Riemann integrable, directly 362Ч363
Riemann Ч Lebesque theorem 513Ч514 538 629
Riesz, F., representation theorem of 120 134 251
Riesz, M. 231
Riordan, J. 656
Risk theory 182Ч183 (see also УRuin problemsФ)
Robbins, H.E. 99 265 360
Rosenblatt, M. 77 287 656
Rotational symmetry 523Ч524
Rotations 78 84 101
RoucheТs Theorem 408
Roulette 22 62
Rounding errors 22 62
Row vectors 83
Royden, H.L. 228
Ruin problems 198 326
Ruin problems in compound Poisson processes 182Ч184 469Ч470
Ruin problems, estimates for 377Ч378 411Ч412
runs see УRecord valuesФ
Rvageva, E.L. 39
Sample extremes and median 18
Sample mean and variance 86Ч87
Sampling theorem 631Ч632 633
Sankhya 571
Savage, L.J. 124 229
Scale parameters 45 134
Scheduling of patients 183
Schelling, H.v. 208
SchloemilchТs formula 60 566Ч567
Schmidt, R. 445
SchwarzТ inequality 152Ч153 166 498 527 642
Second moments 5
Selection theorems 267Ч270
Self-reciprocal functions 503
Self-renewing aggregates 187Т
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте