Àâòîðèçàöèÿ
Ïîèñê ïî óêàçàòåëÿì
Fetter A.L., Walecka J.D. — Quantum theory of many-particle systems
Îáñóäèòå êíèãó íà íàó÷íîì ôîðóìå Íàøëè îïå÷àòêó?
Íàçâàíèå: Quantum theory of many-particle systemsÀâòîðû: Fetter A.L., Walecka J.D. Àííîòàöèÿ: "Singlemindedly devoted to its job of educating potential many-particle theorists ... deserves to become the standard text in the field." — "Physics Today. "The most comprehensive textbook yet published in its field and every postgraduate student or teacher in this field should own or have access to a copy." — "Endeavor. A self-contained treatment of nonrelativistic many-particle systems, this text discusses both formalism and applications. Chapters on second quantization and statistical mechanics introduce ground-state (zero-temperature) formalism, which is explored by way of Green's functions and field theory (fermions), Fermi systems, linear response and collective modes, and Bose systems. Finite-temperature formalism is examined through field theory at finite temperature, physical systems at finite temperature, and real-time Green's functions and linear response. Additional topics cover canonical transformations and applications to physical systems in terms of nuclear matter, phonons and electrons, superconductivity, and superfluid helium as well as applicati
ßçûê: Ðóáðèêà: Ôèçèêà /Ñòàòóñ ïðåäìåòíîãî óêàçàòåëÿ: Ãîòîâ óêàçàòåëü ñ íîìåðàìè ñòðàíèö ed2k: ed2k stats Ãîä èçäàíèÿ: 2003Êîëè÷åñòâî ñòðàíèö: 601Äîáàâëåíà â êàòàëîã: 14.09.2005Îïåðàöèè: Ïîëîæèòü íà ïîëêó |
Ñêîïèðîâàòü ññûëêó äëÿ ôîðóìà | Ñêîïèðîâàòü ID
Ïðåäìåòíûé óêàçàòåëü
49 116 128 480 150 148 187 see He II 3- 584 6- 585—586 Addition theorem for spherical harmonics 516 Adiabatic process 187 Adiabatic “switching on” 59—61 289 Analytic continuation 117p 297—298 302—303 493 Angular momentum, review of 581—588 Angular-momentum operator 505 Anomalous amplitudes 489 Anomalous diagrams 289 Anomalous Green’s functions (bosons) 213 Anticommutation relations 16 atoms 116 121 168p 195p 503 508 546 567 BCS coherence length 426 465 469 BCS gap equation see Gap equation BCS theory see Superconductor Bernoulli’s equation 496 Beta decay 350—351 Bethe — Goldstone equation 322 358—366 567 Bethe — Goldstone equation, 360 Bethe — Goldstone equation, and Galitskii equations 377—383 Bethe — Goldstone equation, anomalous eigenvalue 324 Bethe — Goldstone equation, effective-mass approximation 359 Bethe — Goldstone equation, energy shift of pair 371 Bethe — Goldstone equation, ground-state energy of hard-sphere gas 371—374 Bethe — Goldstone equation, ground-state energy of hard-sphere gas, 374 386p Bethe — Goldstone equation, ground-state energy of hard-sphere gas, 371—374 Bethe — Goldstone equation, ground-state energy of hard-sphere gas, power-series expansion 373—374 Bethe — Goldstone equation, hard-core, solution for 363—366 Bethe — Goldstone equation, partial-wave decomposition 386p Bethe — Goldstone equation, self-consistent 358—360 377—378 Bethe — Goldstone equation, square-well, solution for 360—363 Bethe — Goldstone equation, with degenerate states 569—570 Bethe — Salpeter equation 131—139 219 562—565 Bloch wave functions 5 Bogoliubov equations for superconductor 477p Bogoliubov replacement 200 201 203 315 489 Bogoliubov transformation 316n 326—336 527—537 Bohr radius 25 Bohr — Sommerfeld quantization relation 425 484 Boltzmann distribution 39 279 Boltzmann’s constant 36 Bom approximation 188 197p 219 259 345 368 Bom — Oppenheimer approximation 39n0 410 Bose — Einstein condensation 44 198—200 211 481 Bose — Einstein condensation, and superconductors 441 446 476p Bose — Einstein condensation, rigorous derivation of 41n Boson approximation in shell model 526—527 576p Bosons 7 198—223 314—319 479-499 Bosons noninteracting see Ideal Bose gas Bosons noninteracting, number operator 201—202 Bosons noninteracting, perturbation theory 199 207—210 Bosons noninteracting, potential energy 200 205—206 Bosons noninteracting, proper self-energy 211 215 219 Bosons noninteracting, temperature Green’s function 491 Bosons noninteracting, thermodynamic potential 37 38 202 207 Bosons noninteracting, vacuum state 201 Bosons noninteracting, Wick’s theorem 203 223p Bosons, Bethe — Salpeter equation 219 Bosons, charged 223p 336p 500p 501p Bosons, chemical potential 202 206 216 493 Bosons, condensate 200 493 Bosons, condensate, at finite temperature 492—495 Bosons, condensate, moving 223p 336p 501p Bosons, condensate, nonuniform 495—499 Bosons, density correlation function 223p Bosons, distribution function 37 218 317 Bosons, Dyson’s equations 211—214 223p Bosons, Feynman rules, in coordinate space 208—209 Bosons, Feynman rules, in momentum space 209—210 223p Bosons, field operator 200 Bosons, Green’s functions 203—215 Bosons, ground-state energy 31p 201 207 318 Bosons, hamiltonian 200 315 Bosons, Heisenberg picture 204 Bosons, Hugenholtz — Pines relation 216 220 222 223p Bosons, interaction picture 207—208 Bosons, kinetic energy 205 Bosons, Lehmann representation 214—215 Bosons, momentum operator 204 Brueckner — Goldstone theory and thermodynamic potential 288—289 Brueckner’s theory 116 357—377 382—383 bulk modulus 30 390 407 Bulk property of matter 22 349 canonical ensemble 33 Canonical momentum 424—425 Canonical transformation to particles and holes 70—71 118p 332 504—508 547 Charge-density operator 188 353 Charged Bose gas 223p 336p 500p 501p chemical potential 34 40 75 107 327 528—532 535 Chemical potential, and proper self-energy 107 Chemical potential, bosons 202 206 216 493 Chemical potential, bosons, hard-sphere gas 220—222 Chemical potential, bosons, ideal 39—41 43 Chemical potential, classical limit 39—40 Chemical potential, difference in superconducting and normal state 335 453n Chemical potential, electron gas 278 284—285 Chemical potential, fermions, hard-sphere gas 174 Chemical potential, fermions, ideal 45—48 75 284—285 Chemical potential, phonons 393 410p 485—486 Circulation 483 498 Clausius — Clapeyron equation 499—500p Clebsch — Gordan coefficients 544 582—584 Closed fermion loops 98 103 Coefficients of fractional parentage 523n 576p Coherence length, BCS 426 465 469 Coherence length, Ginsburg — Landau theory 433 472 Coherence length, superconductor 422 426 433 472 Collective modes 171 183 193—194 538 Collision time 184 Commutation relations 12 19 Compressibility 30 222 387p 390—391 condensate 33 200 220 317 491 Condensate, and superfluid density 495 Condensate, ideal Bose gas 42 Condensate, in a channel 502p Condensate, measurement of 495 Condensate, moving 502p Condensate, surface energy 497—498 Condensate, wave function 489 492 Condensate, wave function, at finite temperature 494—495 Condensate, wave function, boundary condition 496 Condensate, wave function, Hartree equation for 490 Condensate, wave function, spatial variation of 497 Condensation energy of superconductor 419 453 Configuration space 7 Connected diagrams 113 301—302 Constant of the motion 59 Continuity equation 183 420 496 Contractions 87—89 238 327—329 Cooper pairs 320—326 359—360 417 441 Cooper pairs, binding energy 325 336 Cooper pairs, bound-state wave function 336p Core-polarization potential 574 577p Correlation energy 29 155 163—166 169p 286—287 Correlation energy, and dielectric function 154 Correlation energy, and polarization propagator 152 Correlations, in nuclei 362—363 365—366 572-573 Correlations, two-particle 191—192 Coulomb energy of nuclei 350 Coulomb interaction 22 188 Coupling-constant integration 70 231—232 280 379 Creation operators 12 Critical angular velocity 499 500p Critical current 476p Critical field 415 451 453 474p Critical temperature of Bose gas 40 259—261 Critical velocity 46n0 482 487 500p Cross section, scattering 189 191 314—315 Crystal lattice 21 30 333 389 390 394—396 Curie’s law 254p 309p 500p Current operator 455 Cyclic property of trace 229 Damping 81 119p 181 195p 308 309p 310p Debye frequency 333 394 395n 396 44n0 Debye shielding length 279 306—308 Debye temperature 394—395 448 Debye theory of solids 389 393—395 Debye — H 278—281 290p Deformed nuclei 515 Degeneracy factor 38 45 Delta function 101 246 Density correlation function 151 174 217 300—303 558 Density correlation function, analytic properties 181n 302—303 Density correlation function, and polarization 153—154 302 Density correlation function, at finite temperature 300—302 Density correlation function, for bosons 223p Density correlation function, for fermions 194p 302 309p Density correlation function, Lehmann representation 300—301 Density correlation function, perturbation expansion 301—302 Density correlation function, relation to polarization propagator 153 302 Density correlation function, retarded 173 194p 300—301 307 Density correlation function, time-ordered 174 175 Density fluctuation operator 117p 189 Density, of 480 Density, of free Fermi gas 26—27 Density, of nuclear matter 348—352 Density, of states 38 266—267 333 447 Depletion 221 317 488 Destruction operators 12 Deuteron 343 Deviation operator, for bosons 489 Deviation operator, for density 151 173 300 560 Diagrams see Feynman diagrams diamagnetic susceptibility 477p Dielectric function 111 154 184 396 Dielectric function, ring approximation 156 163 175 180 Digamma function 580 Dipole sum rule 552 577p Direct-product state 13 17 Disconnected diagrams 94—96 111 301 560 Disconnected diagrams, factorization of 96 Dispersion relation(s), for plasma oscillations 181—182 310p Dispersion relation(s), for propagators 79 191 294—295 Dispersion relation(s), for zero sound 183—184 Distribution function, for bosons 37 218 317 Distribution function, for fermions 38 46 333—334 Distribution function, for moving system 486 500p Dyson’s equations, at finite temperature 250—253 412p Dyson’s equations, for bosons 211—214 223p Dyson’s equations, for electron-phonon system 402—406 411p Dyson’s equations, for Green’s function 105—111 Dyson’s equations, for polarization 110—111 119p 252 271 Dyson’s equations, for superconductors 476p Dyson’s equations, Hartree — Fock approximation 122—123 Effective interaction 155 166—167 252—253 Effective mass, electron gas 169p 310p Effective mass, in nuclear matter 356 369—370 Effective mass, in superconductor 431 Effective mass, of imperfect Bose gas 260 Effective mass, of imperfect Fermi gas 148 168p 266 Effective range 342—343 386p Effective-mass approximation 359 384 Eikonal approximation 468—469 474 Electric quadrupole operator 514 Electron gas, adiabatic bulk modulus 390 Electron gas, chemical potential 278 284—285 Electron gas, classical limit 275—281 290p Electron gas, correlation energy 29 155 163—166 169p 286—287 Electron gas, coupling to background 389 396—406 Electron gas, degenerate 21—31 151—167 281-289 Electron gas, dielectric constant 154 Electron gas, dimensionless variables for 25 Electron gas, effective interaction 155 166—167 Electron gas, effective mass 169p 310p Electron gas, electrical neutrality 25 Electron gas, ground-state energy 32p 151—154 281—289 Electron gas, hamiltonianfor 21—25 Electron gas, Hartree — Fock approximation 289p Electron gas, heat capacity 289—290p Electron gas, Helmholtz free energy 280 284—285 Electron gas, linear response 175—183 303—308 Electron gas, plasma oscillations 180—183 307—308 Electron gas, polarized 32p Electron gas, proper self-energy 169p 268—271 Electron gas, screening 175—180 195p 303—307 Electron gas, single-particle excitations 310p Electron gas, thermodynamic potential 268 273—275 278 284 Electron gas, zero-temperature limit 281—289 Electron scattering 171 188—194 348—349 557 566 Electron-phonon system, chemical potential of phonons 410p Electron-phonon system, coupled-field theory 399—406 Electron-phonon system, coupled-field theory, Dyson’s equations 402—406 411p Electron-phonon system, coupled-field theory, Feynman — Dyson perturbation theory 399—406 Electron-phonon system, coupled-field theory, proper electron self-energy 402 411p Electron-phonon system, coupled-field theory, proper phonon self-energy 402 411p Electron-phonon system, coupled-field theory, vertex part 402—406 Electron-phonon system, equivalent electron-electron interaction 401—402 Electron-phonon system, Feynman rules for 399—401 Electron-phonon system, field expansions 396—397 Electron-phonon system, finite-temperature properties 412p Electron-phonon system, ground-state energy shift 399 411p Electron-phonon system, hamiltonian 398 Electron-phonon system, interaction 320 396—399 417 Electron-phonon system, linear response 412p Electron-phonon system, Migdal’s theorem 406—410 Electron-phonon system, phonon field 410p Electron-phonon system, phonon Green’s function 400 402 411p Electron-phonon system, screened coulomb interaction 397 Electron-phonon system, superconducting solutions 44n0 476p Electronic mean free path 425 Electronic specific heat 395n Energy gap, in nuclear matter 360 383—385 388p Energy gap, in nuclei 385 526 533 Energy gap, in superconductors 320 330 417 447—449 Ensemble average 36 entropy 34—35 Entropy, of an ideal quantum gas 49p Entropy, of He II 486 Entropy, of ideal Fermi gas 48 Entropy, of imperfect Fermi gas 265—266 Entropy, of superconductor 419 476p Equation of motion 253p Equation of state 187 Equation of state, of electron gas 30 278—281 Equation of state, of ideal Bose gas 39 42 Equation of state, of ideal classical gas 39 Equation of state, of ideal Fermi gas 45 46 47—48 Equation of state, of ultrarelativistic ideal gas 49p Equations of motion, linearization 440—441 538—543 Equilibrium thermodynamics and temperature Green’s function 227 229—232 Equipartitionof energy 394—395 Euler’s constant 580 Exchange energy 29 94 126—127 168p 354 Excitation spectrum 81 Excitation spectrum, in normal state 334 Excitation spectrum, in superconductors 334 334n Excitation spectrum, interacting Bose gas 217 317 Exclusion principle see Pauli exclusion principle Extensive variables 29 35 External perturbation 118p 122 172 173 253p 298 303 Factorization of ensemble averages 441 457 Fadeev equations 377 Fermi gas, interacting see Hard-sphere Fermi gas; Interacting Fermi gas Fermi gas, noninteracting see Ideal Fermi gas
Ðåêëàìà
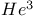, liquid 
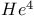, liquid 
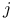symbol 
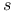-wave 
-wave interactions 
ckel theory 
|
|
Î ïðîåêòå