|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gorenstein D., Lyons R., Solomon R. Ч The Classification of the Finite Simple Groups |
|
|
 |
| ѕредметный указатель |
Group, p-constrained 20
Group, p-solvable 24
Group, perfect 16
Group, quasisimple 16 53 81
Group, semisimple 16
Group, simple, table of 8Ч10
Group, solvable 13 16 73Ч74
Group, sporadic see УSporadic groupФ
Groups in 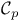 see У see У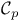 -groupsФ -groupsФ
Groups in 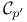 see У see У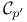 -groupsФ -groupsФ
Groups in 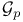 see У see У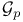 -groupsФ -groupsФ
Groups in 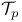 see У see У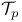 -groupsФ -groupsФ
Groups of 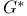 -type ( -type (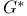 a target group), groups of 2-amalgam a target group), groups of 2-amalgam 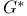 -type, -type,  115 115
Groups of 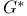 -type ( -type (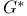 a target group), groups of 2-central a target group), groups of 2-central 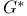 -type, -type,  of Lie type 111 of Lie type 111
Groups of 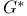 -type ( -type (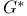 a target group), groups of 2-maximal a target group), groups of 2-maximal 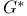 -type mod cores, -type mod cores,  111 111
Groups of 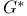 -type ( -type (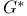 a target group), groups of 2-terminal a target group), groups of 2-terminal 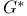 -type, -type,  110 110
Groups of 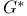 -type ( -type (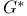 a target group), groups of doubly transitive a target group), groups of doubly transitive 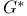 -type, -type,  , , 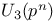 , , 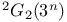 112 112
Groups of 3/2-balanced type 120Ч121
Groups of characteristic 2-type 55 98 116Ч117
Groups of characteristic p-type 25 116Ч117
Groups of even type 36 53Ч55 57Ч59 81 87 98
Groups of generic type 35Ч36 55Ч59 63Ч68 79 106 118Ч121
Groups of generic type, groups of 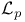 -generic type 57Ч59 61 -generic type 57Ч59 61
Groups of generic type, groups of generic even type 106
Groups of generic type, groups of generic odd type 106
Groups of generic type, groups of semisimple type 121
Groups of generic type, groups of semisimple type, groups of proper semisimple type 121
Groups of GF(2)-type 40Ч43
Groups of large sporadic type 37Ч38 61
Groups of Lie type 6ff. 32ff. 45Ч49
Groups of Lie type as (B,N)-pair 34
Groups of Lie type, Borel subgroup of 33
Groups of Lie type, Bruhat decomposition of 34
Groups of Lie type, Cartan subgroup of 33
Groups of Lie type, Chevalley commutator formula 32
Groups of Lie type, Chevalley group 3
Groups of Lie type, Dynkin diagram of 32 71
Groups of Lie type, generation of 48 65Ч66
Groups of Lie type, Lie rank of twisted 32
Groups of Lie type, Lie rank of untwisted 32
Groups of Lie type, monomial subgroup of 34
Groups of Lie type, monomial subgroup of, reduced 34
Groups of Lie type, parabolic subgroup of 26 62
Groups of Lie type, rank 1 subgroup of 33 35 71
Groups of Lie type, Ree group 3 10 49 50
Groups of Lie type, root subgroup of 32
Groups of Lie type, root system 32
Groups of Lie type, root system, fundamental system 32
Groups of Lie type, Schur multiplier of 45 48
Groups of Lie type, semisimple element of 51
Groups of Lie type, Steinberg presentation of, relations 33
Groups of Lie type, Steinberg variation 7
Groups of Lie type, Suzuki group 3 10
Groups of Lie type, universal version of 33
Groups of Lie type, universal version of and universal covering group 33
Groups of Lie type, untwisted see УChevalley groupФ
Groups of Lie type, Weyl group of 33 35
Groups of odd order, groups of 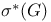 -uniqueness type 107 -uniqueness type 107
Groups of odd order, groups of odd order uniqueness type 107
Groups of odd order, groups of {p,q}-parabolic type 107Ч108
Groups of odd type 58Ч59 81 86
Groups of quasithin type 82 105 114Ч116
Groups of quasithin type, groups of 2-amalgam type 114Ч115
Groups of quasithin type, thin subcase 37 41
Groups of restricted even type 58Ч59 82 90 95 99 102 106
Groups of special type 36Ч38 58Ч61 79 103Ч106 106Ч108 110Ч118
Groups of special type, groups of 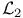 -special type 58Ч60 103Ч104 -special type 58Ч60 103Ч104
Groups of special type, groups of 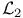 -special type, groups of -special type, groups of  -type 61Ч63 83 104 110Ч113 123 -type 61Ч63 83 104 110Ч113 123
Groups of special type, groups of 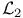 -special type, groups of -special type, groups of  -type, -type,  -subcase 61Ч63 -subcase 61Ч63
Groups of special type, groups of 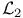 -special type, groups of -special type, groups of 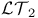 -type 104 114 -type 104 114
Groups of special type, groups of 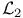 -special type, groups of -special type, groups of 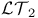 -type, groups of 2-terminal -type, groups of 2-terminal 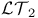 -type 114 -type 114
Groups of special type, groups of 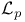 -special type 58Ч60 105Ч106 -special type 58Ч60 105Ч106
Groups of special type, groups of 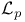 -special type, groups of -special type, groups of  -type 105 116Ч118 -type 105 116Ч118
Groups of special type, groups of 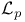 -special type, groups of -special type, groups of  -type, groups of quasisymplectic -type, groups of quasisymplectic  -type 117 -type 117
Groups of special type, groups of 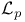 -special type, groups of -special type, groups of  -type, groups of wide -type, groups of wide  -type 116 133Ч135 -type 116 133Ч135
Groups of special type, groups of 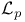 -special type, groups of -special type, groups of  -type 106 118 -type 106 118
Groups of special type, groups of 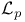 -special type, groups of -special type, groups of  -type, groups of p-terminal -type, groups of p-terminal  -type 118 -type 118
Groups of special type, groups of 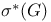 -uniqueness type 107 -uniqueness type 107
Groups of special type, groups of odd order uniqueness type 107
Groups of special type, groups of special even type 105 106 114Ч118
Groups of special type, groups of special odd type 103Ч104 106Ч108 110Ч114
Groups of special type, groups of {p,q}-parabolic type 107Ч108
Groups with specified 2-structure, groups of 2-rank at most 2 36 135
Groups with specified 2-structure, groups of 2-rank at most 3 50
Groups with specified 2-structure, groups with semidihedral or wreathed Sylow 2-subgroups 76 136Ч137
Groups with specified 2-structure, groups with semidihedral or wreathed Sylow 2-subgroups, Brauer group order formula for regular groups 137
Groups with specified 2-structure, groups with semidihedral or wreathed Sylow 2-subgroups, characteristic power 136Ч137
Hall  -subgroup 25 -subgroup 25
Hall, M. 11
Hall, P. 16 25
Harada, K. 11 39 89
Hayashi, M. 37
HE 9 11
Holt, D. 89
HS 9 11
Hunt, D. 49
Huppert, B. 46 47
Identification of simple groups see УRecognition of simple groupsФ
Inn(X) 13
Int, Int(x) 14
Involution fusion pattern 46 60 62 109 110
Isaacs, I. M. 46 47
Isomorphism question 11
J(P) 26 130
Janko, Z. 11 49
k-balance, weak k-balance 124
k-balanced signalizer functor, weakly k-balanced signalizer functor 125
K-groups 5 12
K-groups, theory of 12 45 48 75Ч76 138Ч139
K-proper group 12 75Ч76 79
Klinger Ч Mason method 61 105 116Ч118
Klinger, K. 38 116Ч117
L(X) 139
Layer 17 (see also Уp-layerФ)
Leech lattice 11 35
Lie rank (twisted or untwisted) 32
Linear group 18
Local 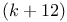 -balance 126 -balance 126
Local balance 128
Local k-balance, weak local k-balance 126
Local subgroup 19 (see also Уp-local subgroupФ)
Local subgroup, general structure of 27Ч28
Lp'-balance 21
Ly 9 11
Lyons, R. 41 48Ч50 99
m(X) 139
Mason, G. 37Ч38 41 116Ч117
Mathieu, E. 11
Maximal subgroup 60 62Ч63 123
Mc 9 11
McBride, P. 30 49 124
Meierfrankenfeld, U. 130
Meighbor, (y, I)-neighbor 64 119
Modules, failure of factorization 26 130 133
Modules, quadratic 25Ч26 123 130
Monomial subgroup 34
N-group 38Ч39 73
Near component 50 96Ч97 129Ч131 133
Near component (of Y ): linear, alternating, standard 96 98
Near component 2-local uniqueness subgroup 97
Near component, alternating 96Ч97 130
Near component, associated module of 96
Near component, linear 96Ч97 130 131
Near component, standard 98
Near component, type 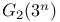 97 97
Neighbor 42 64Ч65 71 119
Neighbor, semisimple 64Ч65
Neighborhood 55Ч58 59 63Ч68 118Ч120
Neighborhood,  61 117 61 117
Neighborhood, base of 119
| Neighborhood, example of 56Ч57 68Ч70
Neighborhood, level 66 121
Neighborhood, span of 66Ч67 121
Neighborhood, vertical 65 76Ч77 118Ч120
Neighborhood: level, split, vertical 65 119 120
Niles, R. 39 50
Notation 139
Notation for simple groups 8 9
O'N 9 11
O(X),  , ,  , ,  19 19
Odd type 58Ч59 81
Odlyzko, A. 49
Out(X) 29
Outer automorphisms 18
Overall strategy of proof 35Ч38 42Ч43
OТNan, M. 18 45 49 138
p'-core 19; (see also УCoreФ)
p'-core, elimination 23Ч24 37 61 120
p'-core, embedding of p'-core of p-local subgroups 21 127Ч128
p-central element of order p 101
p-central p-element 101
p-component 20
p-component preuniqueness hypothesis 91Ч92
p-component preuniqueness subgroup see УUniqueness subgroupsФ
p-component uniqueness theorems 30Ч31 38 53 65 90Ч92 118
p-component, p-terminal 22ff. 63 108Ч109
p-component, p-terminal, pumping up to 23 108Ч109
p-component, solvable 64 109
p-constrained group 20
p-layer 20
p-local subgroup 19
p-local subgroup, embedding of p'-core of 20Ч21 127Ч128
p-local subgroup, embedding of p-layer of 21Ч24 127
p-solvable group 24
p-source 64
p-terminal 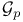 -pair 63 -pair 63
p-terminal  -type 118 -type 118
p-terminal p-component 23 108
p-uniqueness subgroup 82
Parts of the series 4Ч5 59 77Ч78 80
Parts of the series, Part II 38 52Ч53
Parts of the series, Part III 36
Parts of the series, Part IV 37
Parts of the series, Part V 37 38
perfect central extension see УCovering groupФ
Permutation group 18 35
Permutation group, doubly transitive 74 112Ч113 138
Permutation group, doubly transitive of Suzuki type 95Ч96
Permutation group, doubly transitive, split (B,N)-pair of rank 1 95Ч96 112Ч113 138
Permutation group, highly transitive 11 35
Permutation group, of rank 3 11
Permutation group, representation as 31
Peterfalvi, T. 48Ч49 96 107 138
Phan, K.-W. 35 71
Presentation 31Ч35
Presentation of classical groups 35
Presentation of symmetric groups 32 36 68Ч70
Presentation, Steinberg presentation of groups of Lie type 32 33 36 51 118
Presentation, Steinberg presentation of groups of Lie type, a la Curtis Ч Tits 34 67 70
Presentation, Steinberg presentation of groups of Lie type, a la Gilman Ч Griess 35 67 71
proper 2-generated core 89
proper semisimple type 121
Pumpup 22 127
Pumpup as 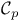 , , 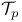 , or , or 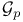 -group 103 114 -group 103 114
Pumpup, diagonal, proper, trivial, or vertical 22 127
Pumpup: vertical, trivial, diagonal, proper 22 127
Quadratic  -module 25 -module 25
Quadratic chief factor 26
Quasisimple group 16 53 81
Quasisymplectic type 117
Quasithin 5 37 41 43 60Ч61 82 105 114Ч116
Quasithin, quasithin type, quasithin case 60 82
Recognition of simple groups 31Ч35
Recognition of simple groups, alternating groups 32
Recognition of simple groups, groups of Lie type 32Ч35 42 49 137Ч138
Recognition of simple groups, recognition of symmetric groups 68Ч70
Recognition of simple groups, sporadic groups 35
Reduced monomial subgroup 34
Ree group 10
Ree groups 3 10 49 50
Ree, R. 10
Regular 136
Restricted even type 95
Root subgroup, root system 32
Rowley, P. 37
Ru 9 11
S(G) 29
Schreier property 21 24 29
Schreier, O. 21
Schur multiplier 18 45 48 139
Schur, I. 17
Scott, L. 18
Section 12
Seitz, G. 48
Semisimple group 16
Semisimple neighbor 64
Semisimple type 121
Sibley, D. 48
Signalizer functor 29Ч30 124ff.
Signalizer functor method 29Ч30 36Ч38 41 60 64Ч65 104Ч105 116 118 120 128Ч129
Signalizer functor, closed 124
Signalizer functor, closure 30 124
Signalizer functor, complete 124
Signalizer functor, k-balanced, weakly k-balanced 124Ч126
Signalizer functor, solvable 124
Signalizer functor, trivial 124 128
Signalizer functor: A-signalizer functor, solvable, closed, complete 124
Simple group 13
Simple groups, table of 8Ч10
Simplicity criteria 29Ч31
Sims, C. 39 45
Sims, conjecture 74
Smith, F. 41
Smith, S. 41
Solomon, R. 35 39 53
Solvable component, solvable p-component 109
Solvable group 13
Span of 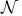 66 121 66 121
Special even type 105
Special odd type 103
Special, special type 58
Spor 81
Sporadic groups 3 6 9 11 87 100
Sporadic groups as 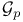 -group 103 -group 103
Sporadic groups as target group 77 87
Sporadic groups, background properties of 44Ч48 50
Sporadic groups, existence and uniqueness of 46Ч47 50 72
Sporadic groups, individual groups, Baby Monster  11 38 87 100 11 38 87 100
Sporadic groups, individual groups, Conway groups  , ,  , ,  11 38 42 72 87 100 11 38 42 72 87 100
Sporadic groups, individual groups, Fischer 3-transposition groups 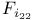 , , 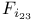 , , 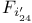 11 38 87 100 11 38 87 100
Sporadic groups, individual groups, Fischer Ч Griess Monster 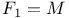 3 11 38 42 47 61 72 87 100 3 11 38 42 47 61 72 87 100
Sporadic groups, individual groups, Harada Ч Norton 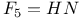 11 67Ч68 87 100 11 67Ч68 87 100
Sporadic groups, individual groups, Held He = HHM 11 87 100
Sporadic groups, individual groups, Higman Ч Sims HS 11 87 100
Sporadic groups, individual groups, Janko 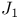 , ,  , , 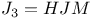 , , 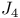 3 11 87 100 3 11 87 100
Sporadic groups, individual groups, Lyons Ч Sims Ly 11 45 87 100
Sporadic groups, individual groups, Mathieu  , , 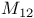 , , 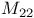 , , 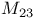 , , 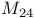 11 42 46 72 87 100 11 42 46 72 87 100
Sporadic groups, individual groups, McLaughlin Mc 11 87 100
Sporadic groups, individual groups, OТNan-Sims O'N 11 87 100
Sporadic groups, individual groups, Rudvalis Ru 11 87 100
Sporadic groups, individual groups, Suzuki Suz 11 87 100
Sporadic groups, individual groups, Thompson  11 87 100 11 87 100
Standard component 53
Standard form problems 38
Standard preuniqueness subgroup 91
Steinberg presentation, relations 32Ч33
Steinberg variation 10
Steinberg, R. 3 7 10 17 45 47 48
Stellmacher, B. 37 50
Strong p-uniqueness subgroup 52 94
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



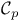
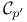
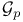
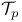
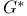 -type (
-type (
 of Lie type
of Lie type 
 ,
, 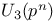 ,
, 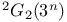
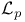 -generic type
-generic type 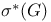 -uniqueness type
-uniqueness type 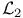 -special type
-special type  -type
-type  -subcase
-subcase 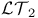 -type
-type  -type
-type  -type
-type  -subgroup
-subgroup 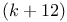 -balance
-balance 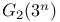

 ,
,  ,
, 
 -module
-module 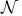

 ,
,  ,
, 
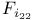 ,
, 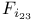 ,
, 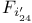
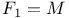
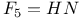
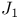 ,
,  ,
, 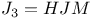 ,
, 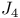
 ,
, 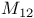 ,
, 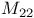 ,
, 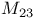 ,
,