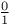|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Oldham K., Spanier J. — The fractional Calculus: Theory and applications of differentiation and integration to arbitrary order |
|
|
 |
| Предметный указатель |
Abel's integral equation 2 4 9 13 183—186
Abel, N.H. 2 4 183 184 219
Abramowitz, M. 219
Airy functions 180
Airy functions as hypergeometrics of complexity 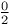 164 164
Algorithms for differintegration 136—148
Allegre, J. 133 202 219
Analog differintegration 148—154
Analytic functions 77 80 116
Analytic functions, differintegrals of 75
Applications of fractional calculus, to Abel's integral equation 183—186
Applications of fractional calculus, to biology 10
Applications of fractional calculus, to chemical physics 2
Applications of fractional calculus, to classical calculus 181—195
Applications of fractional calculus, to definition of function families 192—195
Applications of fractional calculus, to differential equations 2 8 10 13
Applications of fractional calculus, to diffusion of atmospheric pollutants 208
Applications of fractional calculus, to diffusion problems 197—218
Applications of fractional calculus, to electrical conduction in transmission lines 210
Applications of fractional calculus, to electrochemistry 2 14 15 204
Applications of fractional calculus, to functional equations 10
Applications of fractional calculus, to geometry 4
Applications of fractional calculus, to grain boundary grooving in metals 216—218
Applications of fractional calculus, to integral equations 2 10 12 13 15
Applications of fractional calculus, to location of candidate solutions for differential equations 189—192
Applications of fractional calculus, to mechanics 4
Applications of fractional calculus, to Navier — Stokes equation 12 14
Applications of fractional calculus, to prediction of peak pollutant concentrations 209
Applications of fractional calculus, to problems of elasticity 2
Applications of fractional calculus, to quantitative chemical analysis 205—207
Applications of fractional calculus, to rheology 2
Applications of fractional calculus, to solution of Bessel's equation 186—189
Applications of fractional calculus, to solution of Legendre's equation 191
Applications of fractional calculus, to tautochrone problem 2 4 5
Applications of fractional calculus, to theory of heat conduction 202—203
Applications of fractional calculus, to transmission line theory 2
Applications of fractional calculus, to transport problems 2
Applications of fractional calculus, to wave equation 11
Associated Legendre functions, as reducible transcendentals 161
Ayabe, Y. 160 221
Babbitt, J.D. 197 219
Barrer, R.M. 197 219
Basic hypergeometrics, definition of 168
Basic hypergeometrics, graphs of 168
Basic hypergeometrics, Laplace transformation of 171
Basic hypergeometrics, relationships among 171
Basis hypergeometrics 168—172
Basis hypergeometrics, complementary 168
Bassam, M.A. 12
Belavin, V.A. 2 13 219
Berg, E.J. 9
Bessel functions 13 97—98 124 125 177—178
Bessel functions as hypergeometrics of complexity 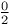 164 164
Bessel functions as reducible transcendentals 161
Bessel functions, relationships among 98
Bessel's equation 186—189
Bessel's equation, solution via fractional calculus 186—189
beta function see "Complete beta functions" "Incomplete
Bibliography, chronological 3—15
Binomial coefficients 20 28—29 178 180
Binomial coefficients of moiety argument, table of 118
Binomial functions 162 174
Binomial functions as hypergeometrics of complexity 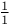 99 99
biology 10
Biorci, G. 154 219
Bishop, D.M. 2 14 222
Blumenthal, L.M. 10
Boole, G. x 2 6 219
Boundary geometries for diffusion problems 198
Boundary geometries for diffusion problems, diagrams of 199
Bourlet, C. x 2 219
Brenke, W.C. 9
Buschman, R.G. 12 13
Butzer, P. 14
Caffyn, J.E. 2 222
Carslaw, H.S. 197 219
Carson, J.R. 2 219
Cauchy's integral formula 1 7 8 14 54
Cayley, A. 8
Center, W. 6 7 9
Chain rule for differintegrals 80—81
Chain rule for multiple derivatives 36—37
Chronological bibliography on fractional calculus 3—15
Churchill, R.V. 134 136 150 219
Circuit for performing semiintegration see "Semiintegrating circuits"
Civin, P. 53 219
Classical calculus 25—44
Classical derivatives 28
Classical integrals 29
Cole, K.S. 10
Complementary functions 4 5 8
Complete beta functions 21 65
Complex error functions 209
Composition rule 48 82—87
Composition rule for differentiable functions 85
Composition rule for differentiable functions, tabular summary 86
Composition rule for differintegrable units 82—84
Composition rule for differintegrable units, tabular summary 84
Composition rule for general differintegrable series 84—85
Composition rule for general differintegrable series, tabular summary 85
Composition rule for mixed integer orders 30—33
Composition rule for mixed integer orders, failure 32
Composition rule for noninteger orders 63
Composition rule, examples illustrating failure 83 86—87
Composition rule, role in locating solutions of differential equations 190
Composition rule, use in inverting extraordinary differential equations 155
Composition rule, utility in finding differintegrals 96
Continued fractions 151—152
Convolution theorem for Laplace transformation 134
Cosine integrals as reducible transcendental 161
cosines see "Sines and cosines"
Coulomb's law 211
Courant, R. 12 27 50 219
Crank, J. 197 219
Curvature correction for current semiintegral, graph of 206
Cyclodifferential functions 110—112 169(n)
Cyclodifferential functions, definition of 110
Cycloid as solution to tautochrone problem 185
Cycloid as solution to tautochrone problem, diagram of 185
Davis, H.T. 8 9 10 11
Davison, B. 197 219
Dawson's integral 163 175
Definite integrals, evaluation through fractional calculus 181—183
Delahay, P. 160 219
Delta function see "Dirac delta function"
DeMorgan, A. 5
derivatives see "Classical derivatives"
Difference quotients 28 48 56
Difference quotients for classical derivatives 28
Differential equations 2 8 10 13
Differential equations, conversion to lower order 190
Differentiation of hypergeometrics 40—44
Differentiation of powers 39—40 192
Differentiation of powers, diagram showing sign of resultant derivative 39
Differentiation to fractional order see "Differintegration"
Differentiation, term by term 38
Differintegrable and nondifferintegrable functions, figure showing examples of each 47
Differintegrable functions 46—47
Differintegrable functions, definition of 47
Differintegrable series 69 70 82 93 116
Differintegrable series units 82
Differintegrable series units, definition of 46
Differintegrable series, definition of 46
Differintegral operators of imaginary order 14
Differintegral operators of integer order 25—44
Differintegral operators with respect to arbitrary function 55
Differintegral operators, analytic continuation for 49
Differintegral operators, comparison of definitions 55—57
Differintegral operators, connection with Fourier analysis 56
Differintegral operators, connection with Laplace transformation 11
| Differintegral operators, defined x 16 27(n)
Differintegral operators, definition of 45—60
Differintegral operators, definition of, as integral transform see "Differintegral operators" "Riemann
Differintegral operators, definition of, as sum see "Differintegral operators" "Gruenwald
Differintegral operators, definition of, based on Cauchy's integral formula 54 56
Differintegral operators, definition of, based on Cauchy's integral formula, diagram of contour used 55
Differintegral operators, definition of, in terms of difference quotients 1
Differintegral operators, definition of, in terms of series 1 5 7 53
Differintegral operators, differentiation of 48 50
Differintegral operators, equivalence of definitions 51—52
Differintegral operators, general properties 10 11 69—92
Differintegral operators, general properties, behavior far from lower limit 91
Differintegral operators, general properties, behavior near lower limit 90
Differintegral operators, general properties, chain rule 14 80—81
Differintegral operators, general properties, commutativity 87
Differintegral operators, general properties, composition rule 82—87
Differintegral operators, general properties, dependence on lower limit 87—89
Differintegral operators, general properties, differintegration term by term 69—75
Differintegral operators, general properties, homogeneity 75
Differintegral operators, general properties, inversion 86
Differintegral operators, general properties, Leibniz's rule 76—79
Differintegral operators, general properties, linearity 69
Differintegral operators, general properties, scale Differintegral operators, general properties, change 75—76
Differintegral operators, general properties, translation 89—90
Differintegral operators, Gruenwald definition 48 55
Differintegral operators, identity of definitions 51—52
Differintegral operators, modified Gruenwald definition 57
Differintegral operators, representation for analytic functions 57—59
Differintegral operators, Riemann — Liouville definition 1 6 9 56 see
Differintegral operators, Riemann — Liouville definition, use in evaluating integrals 181
Differintegral operators, some general definitions 52—57
Differintegral operators, summary of definitions 59—60
Differintegral operators, symbolism for 45
Differintegration 61—68 93—114
Differintegration of Bessel functions 97—98
Differintegration of binomial functions ![$[C-cx]^{p}$](/math_tex/30f3d96d3627211edc6f93ff4e4e5a4382.gif) 93—94 93—94
Differintegration of constants 63
Differintegration of cosine function cos(x) 112
Differintegration of cyclodifferential functions 110—112
Differintegration of Dirac delta function 106
Differintegration of exponential functions exp(C-cx) 94—95
Differintegration of function 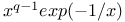 112—113 112—113
Differintegration of function x-a 63—65
Differintegration of functions ![$x^{q}/[1-x]$](/math_tex/ca814f5354f1fbdbcab1d8c0cde6816c82.gif) and and ![$x^{p}/[1-x]$](/math_tex/d8111eaf191b06ca72ed8f0327c21cf282.gif) and and ![$[1-x]^{q-1}$](/math_tex/2c4ff7facf28fb99bfdf65c696ee0dc082.gif) 1 95—96 1 95—96
Differintegration of Heaviside function 105
Differintegration of Heaviside function, diagram illustrating 106
Differintegration of hyperbolic function sinh(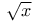 ) 96—97 ) 96—97
Differintegration of hypergeometric functions 99—102
Differintegration of hypergeometric functions, examples of 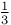 complexity 112 complexity 112
Differintegration of logarithms 102—104
Differintegration of periodic functions 108—110
Differintegration of piecewise-defined functions 107
Differintegration of powers 63—68
Differintegration of powers, breakdown for p<= -1 67
Differintegration of powers, figure showing contour used in 66
Differintegration of powers, signs of resulting coefficients 68
Differintegration of sawtooth function 107—108
Differintegration of sawtooth function, diagram of 108
Differintegration of sine function sin(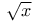 ) 96—97 ) 96—97
Differintegration of sine function sin(x) 112
Differintegration of unit function 61—63
Differintegration of unit function, graphs of differintegrals 62
Differintegration of zero function 63
Differintegration to order one-quarter 217
Diffusion equation for semiinfinite geometries 199
Diffusion equation in presence of sources and sinks 207
Diffusion equation, general form 198
Diffusion in finite media 209—215
Diffusion in planar geometry 201—203
Diffusion in presence of sources and sinks 207—209
Diffusion in spherical geometry 204—207
Diffusion on curved surface 216—218
Dirac delta function 105
Dirac delta function, differintegrals of 106
Duff, G.F.D. 27 49 220
Eigenfunction of differintegral operator 122(n)
Eigenfunction of semidifferential operator 122(n)
Eigenfunction of semidifferential operator, graph of 123
Elasticity 2
Electrochemistry 2 14 15 204
Elliptic integrals as hypergeometrics of complexity 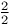 165 165
Elliptic integrals as reducible transcendentals 161
Elliptic integrals of first kind 122
Elliptic integrals of second kind 122
Erdelyi, A. 2 11 12 13 54 55 76 115 220
Error function complement 194
Error function complement integrals 175 194—195
Error functions 175
Error functions as reducible transcendentals 161
Errors in analog semidifferentiation 215—216
Errors in analog semidifferentiation, graph of, for various terminations 215
Euler's constant 24
Euler's integral of second kind 21
Euler, L. 1 3 220
Exponential functions, differintegration of 94—95
Exponential integrals 166
Exponential integrals as reducible transcendentals 161
Exponential-like functions, as hypergeometrics of complexity 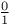 162 162
Extraordinary differential equations 154—157
Extraordinary differential equations for describing groove depth in metals 217
Extraordinary differential equations, definition of 154
Extraordinary differential equations, inversion of 155
Extraordinary differential equations, series solutions of 159—160
Faa di Bruno's formula for differentiating composite function 37 80
Fabian, W. 11
Faddeeva, V.N. 209 220
Faradaic current, diagram illustrating curvature correction 206
Faradaic current, graph versus time 206
Faradaic current, semiintegral of 205—207
Faraday's constant 204
Faraday's electrochemical law 204
Feller W. x 220
Festinger, J.C. 219
Fick's First Law 204
Fourier analysis 14
Fourier, J.B.J. 4 5
Fractional calculus applications of see "Applications of fractional calculus"
Fractional calculus, historical survey 1—15
Fractional calculus, symbolic methods in 2
Fractional difference operators 12
Fractional differential operators see "Differintegral operators"
Fractional differentiation see "Differintegration"
Fractional integral operators see "Differintegral operators"
Fractional integration see "Differintegration"
Fractional integration by parts 11
Fractional integration for functions of more than one variable 2
Fresnel integrals 125 180
Fresnel integrals as reducible transcendentals 161
Friedman, B. x 220
Function families 192—195
Function synthesis 169
Function synthesis diagrams see "Synthesis diagrams"
Function synthesis of K=L transcendentals 172—175
Function synthesis of K=L-1 transcendentals 175—176
Function synthesis of K=L-2 transcendentals 177—180
Functional equations 10
Fundamental theorem of calculus 30
Gaer, M.C. 13 53 220
Gamma function 14 16—24 see
Gamma function for integer and half-integer arguments 17—18
Gamma function for integer and half-integer arguments, table of values 18
Gamma function, asymptotic expansion 19
Gamma function, duplication formula 18
Gamma function, Gauss multiplication formula 18
Gamma function, general properties 16—24
Gamma function, ratios 17 19—20
Gamma function, ratios, polynomials expressible as 19
Gamma function, ratios, polynomials expressible as, graphs of 19
Gamma function, reciprocal 17
Gamma function, reciprocal, asymptotic representation of 17
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



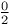
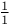
![$[C-cx]^{p}$](/math_tex/30f3d96d3627211edc6f93ff4e4e5a4382.gif)
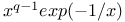
![$x^{q}/[1-x]$](/math_tex/ca814f5354f1fbdbcab1d8c0cde6816c82.gif) and
and ![$x^{p}/[1-x]$](/math_tex/d8111eaf191b06ca72ed8f0327c21cf282.gif) and
and ![$[1-x]^{q-1}$](/math_tex/2c4ff7facf28fb99bfdf65c696ee0dc082.gif)
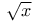 )
) 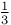 complexity
complexity