|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Oldham K., Spanier J. — The fractional Calculus: Theory and applications of differentiation and integration to arbitrary order |
|
|
 |
| Предметный указатель |
Gamma function, reciprocal, graph of 17
Gamma function, recurrence formula 16
Gamma function, reflection formula 18
Gamma function, relation to beta functions 21
Gamma function, relation to binomial coefficients 20
Gamma function, relation to psi function 23
Gauss functions 41 122 165 174
Gauss functions as reducible transcendentals 161
Gel'fand, I.M. 13
Gemant, A. 2 67 220
Generalized Abel equation 186
Generalized differentiation see "Differintegration"
Generalized differentiation for operators 2
Generalized error function complement integrals 195
Generalized hypergeometric functions see "Hypergeometrics"
Generalized integration see "Differintegration"
Generalized logarithms 163(n) 175 192
Generalized logarithms, definition of 193
Generalized logarithms, representation of 193—194
Geometric factor to characterize boundary geometries in diffusion problems 198
Gradshteyn, I.S. 220
Graham, A. 2 220
Greatheed, S.S. 5
Greer, H.R. 7
Gregory, D.F. 5
Grenness, M. 2 14 144 204 220
Gruenwald, A.K. x 1 7 48 220
Hadamard, J. 8
Hagstrom, K.G. 11
Hardy, G.H. 2 8 9 10 11 220
Hargreave, C.J. 6
Heat conduction in semiinfinite planar medium 202
Heat equation 5
Heat flux, relation to surface temperature through semidifferentiation 202
Heaviside function 61 105
Heaviside function, graph of differintegrals 106
Heaviside's operational calculus see "Operational calculus"
Heaviside's unit function see "Heaviside function"
Heaviside, O. x xii 2 8 9 53 62 220
Herpe, G. 219
Higgins, T.P. 2 13 220
Hilbert transforms 15
Hilbert, D. 27 50 219
Hille, E. x 220 221
Hirschmann, I.I. 12
Holmgren — Riesz transforms 12
Holmgren, H. 1 7 12 221
Holub, K. 133 221
Hyperbolic cosines as reducible transcendental 161
Hyperbolic sine integrals 128
Hyperbolic sine integrals as hypergeometrics of complexity 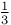 165 165
Hyperbolic sines as hypergeometrics of complexity 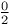 100 100
Hyperbolic sines as reducible transcendentals 161
Hypergeometric functions 11 13 14 15
Hypergeometric functions as reducible transcendentals 161
Hypergeometric functions of complexity 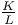 15 15
Hypergeometric functions, Laplace transformation of 171
Hypergeometric functions, notation for 15
Hypergeometric functions, product with power of argument see "Hypergeometrics"
Hypergeometrics 40—41 99—102 129—130
Hypergeometrics as differintegrable series 99
Hypergeometrics as sum of hypergeometrics 44
Hypergeometrics as sum of hypergeometrics, use in finding differintegrals 101
Hypergeometrics of argument 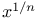 43 100—101 43 100—101
Hypergeometrics of complexity 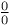 162 162
Hypergeometrics of complexity 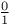 162 162
Hypergeometrics of complexity 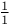 163 163
Hypergeometrics of complexity 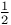 164 164
Hypergeometrics of complexity 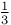 165 165
Hypergeometrics of complexity 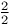 164—165 164—165
Hypergeometrics with K>L 165—166
Hypergeometrics with K>L, utility for asymptotic representations 166
Hypergeometrics, cancellation property of 42
Hypergeometrics, convergence properties of 165
Hypergeometrics, definition of 162
Hypergeometrics, differentiation and integration of 40—44
Hypergeometrics, differintegrals of 99—102
Hypergeometrics, examples of 162—165
Hypergeometrics, Laplace transformation 171—172
Hypergeometrics, recurrence relations for 42
Hypergeometrics, reduction of complexity 166—167
Hypergeometrics, reduction to complexity 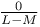 167 167
Hypergeometrics, regeneration from basis hypergeometrics 169
Hypergeometrics, symbolism for 40
I'a Bromwich, T.J. 9
Ichise, M 133 154 221
Incomplete beta functions 21 41 94 122 174
Incomplete beta functions as reducible transcendentals 161
Incomplete gamma functions 21 41 94 95 109 158 175
Incomplete gamma functions as reducible transcendental s 161
Incomplete gamma functions, recursion formula for 22
Infinite series, differentiation and integration of 38
Infinite series, evaluation through fractional calculus 183
Infinite transmission line, approximation by finite transmission line 212
Integral equations 2 10 12 13 15
Integrals see "Classical integrals"
Integrating circuit 149
Integration of hypergeometrics 40—44
Integration of powers 39—40 192—193
Integration of powers, diagram showing sign of resultant integral 39
Integration to fractional order see "Differintegration"
Integration, term by term 38
Intergranular groove 216—218
Intergranular groove, cross sectional diagram 217
Inverse hyperbolic functions 163
Inverse hyperbolic functions as reducible transcendentals 161
Inverse hyperbolic sines as hypergeometrics of complexity 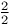 165 165
Inverse trigonometric functions 163
Inverse trigonometric functions as reducible transcendentals 161
Iterated integrals 37—38
Iterated integrals, Cauchy's formula for 38
Jaeger, J.C. 197 219
Johnson, W.C. 197 210 221
Jost, W. 197 221
Juberg, R.K. 15
Kalisch, G.K. 13
Kaufman, H. 115 222
Kelland, P. 4 5 6 7
Kesarwini, R.N. 13
Knopp, K. 49 221
Kober, H. 2 11 14 221
Kojima, T. 221
Koutecky function of polarography 160
Koutecky, J. 160 221
Krug, A. 1 8 53 221
Kummer functions 41 175
Kummer functions as hypergeometrics of complexity 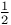 164 164
Kummer functions as reducible transcendentals 161
Kuttner, B. 2 12 221
L'Hospital, G.A. 1 3
Lacroix, S.F. 4
Lagrange, J.L. 1 3 221
Laplace transforms 11 115
Laplace transforms for performing circuit analysis 150
Laplace transforms of derivatives and integrals 133
Laplace transforms of differintegrals 133—136
Laplace transforms of differintegrals, formula for 134
Laplace transforms, role played in solving diffusion problems 201
Laplace, P.S. 3
Laurent, H. 8
Law of exponents see "Composition rule"
Law of exponents, for operators of integral order 3
Lebesgue class 2 10
Legendre functions 122
Legendre functions as hypergeometrics of complexity 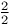 164 164
Legendre functions as reducible transcendentals 161
Legendre's equation 191
Leibniz's rule 6 8 10 14 15 53 62
Leibniz's rule for derivatives 36
Leibniz's rule for differintegral operators, convergence difficulties 78—79
| Leibniz's rule for differintegral operators, integral form 79 182
Leibniz's rule for differintegral operators, symmetric form 79
Leibniz's rule for differintegral operators, when factors are analytic 77
Leibniz's rule for differintegral operators, when one factor is polynomial 77—78
Leibniz's rule for multiple integrals 34—35
Leibniz, G.W. x 1 3 221
Letnikov, A.V. 7 8
Levy, P. 9
Lions, J.L. 12 14
Liouville, J. xi 1 4 5 6 7 8 49 53 95 191 221
Lipschitz classes 2
Littlewood, J.E. 2 10 11 220
Liverman, T.P.G. 13
Logarithms 163
Logarithms as hypergeometrics of complexity 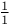 102 102
Logarithms as reducible transcendentals 161
Logarithms, differintegrals of 102—104
Logarithms, differintegrals of, graphs of 104
Logarithms, generalization of 192—194
Logarithms, generalization of, location in function synthesis diagram 194
Love, E.R. 11 14
Lower limit 87—89
Lutskaya, N.K. 13 219
Magnus, W. 220
Matsuda, H. 160 221
Mechanics 4
Mellin transforms 11
Meyer, R.F. 133 203 221
Mikusinski, J.G. x 221
Miroshnikov, A.I. 13 219
Modified Bessel functions 97—98 125
Modified Bessel functions as hypergeometrics of complexity 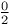 100 100
Modified Struve functions 125
Modified Struve functions, notation for 15
Moore, F.K. 197 221
Moritz, R.E. 8
Mullins, W.W. 217 218 221
Multiple integrals, dependence on lower limit 33—34
Multiple integrals, symbolism for 26 27
Murphy, G.M. 156 158 159 202 221
Muskat, M. 197 221
Nagayanagi, Y. 221
Naraniengar, M.T. 9
Navier — Stokes equation 12 14
Nekrassov, P.A. 8 54 221
Nemec, L. 133 221
Nerve impulse propagation 10 210(n)
Nessel, R. 14
Nigmatullin, R.Sh. 13 219
Numerical differintegration, algorithms for 136—148
Numerical differintegration, algorithms for, based on Gruenwald definition 136
Numerical differintegration, algorithms for, based on linear interpolation 140
Numerical differintegration, algorithms for, based on modified Gruenwald definition 137—138
Numerical differintegration, algorithms for, based on Riemann — Liouville definition 138—139
Numerical differintegration, algorithms for, relative error in 141—144
Numerical differintegration, algorithms for, weighting factors in 144
Numerical differintegration, algorithms for, weighting factors in, table of 146—147
Numerical differintegration, approximations used in, diagram illustrating 139
Numerical differintegration, coincidence of algorithms for 144
Numerical differintegration, comparison of rival algorithms 144—145
Numerical differintegration, comparison of rival algorithms, in differintegrating 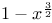 145 148 145 148
Numerical differintegration, comparison of rival algorithms, in differintegrating 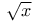 145 145
Numerical differintegration, errors in 141—144
Numerical differintegration, errors in, table of 144
Numerical differintegration, nomenclature for 136
Numerical differintegration, nomenclature for, diagram illustrating 137
O'Shaughnessy, L. 8
Oberhettinger, F. 220
Ohm's law 150 211 214
Oldham, K.B. 2 14 15 133 143 144 154 160 200 204 220 221 222
Oltramare, G. 8
Operational calculus 9 10 11 12 13
Ordinary derivatives see "Classical derivatives"
Ordinary differential equations, solution via fractional calculus 186—189
Ordinary integrals see "Classical integrals"
Osler, T.J. 2 14 15 54 55 56 79 81 182 183 192(n) 222
Parseval's integral formula 79
Peacock, G. 4 6 7 8
Pennell, W.O. 10
Periodic functions 108—110
Periodic functions as hypergeometrics of complexity 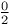 163 163
Peters, A.S. 12
Piecewise-defined functions 105 107—108
Pincherle, S. 8
Poritsky, H. 11
Post, E.L. 2 6 8 9 10 48 222
Prabhakar, T.R. 15
Product rule see "Leibniz's rule"
Psi function 23 103
Psi function, recursion formula for 23
Quasi-semiinfinite medium, condition for 200(n)
Radius of convergence of differintegrable series 70—71
Rayleigh's formulas, generalizations of 97
Reducible transcendentals 161
Resistive-capacitative transmission line see "Transmission line"
Rheology 2 67
Ridella, S. 154 219
Riemann Sums 48 56
Riemann sums for classical integrals 29
Riemann zeta function 142—143
Riemann zeta function, table of values 143
Riemann — Liouville integral 49 55
Riemann — Liouville transforms 115
Riemann, B. xi 1 6 7 49 53 222
Riesz, M. 2 11 12 27 49 222
Ritt, J.F. x 2 222
Roberts, G.E. 115 222
Robertson, W.M. 217 222
Rodrigues' formula, generalization of 192
Ross, B. xiii 3 15
Rubel, L.A. 14 53 220
Ryzhik, I.M. 220
Samko, S.G. 13
Sawtooth function 107—108
Sawtooth function, graphs of differintegrals 108
Scale-change property, use in finding differintegrals 100 109
Schuyler, E. 8
Scott Blair, G.W. 2 53 67 220 222
Semi derivatives 7 50
Semicalculus 14
Semiderivatives and semiintegrals 115—131
Semiderivatives and semiintegrals, definition of 115(n)
Semiderivatives and semiintegrals, graphs for cos(x) 126
Semiderivatives and semiintegrals, graphs for sin(x) 126
Semiderivatives and semiintegrals, role played in solving diffusion problems 197
Semiderivatives and semiintegrals, table of definitions 115—116
Semiderivatives and semiintegrals, table of general properties 116—117
Semiderivatives and semiintegrals, tables of, for Bessel and Struve functions 127—128
Semiderivatives and semiintegrals, tables of, for binomials 120—121
Semiderivatives and semiintegrals, tables of, for complete elliptic integrals 131
Semiderivatives and semiintegrals, tables of, for constants and powers 118—119
Semiderivatives and semiintegrals, tables of, for exponentials and related functions 122—124
Semiderivatives and semiintegrals, tables of, for generalized hypergeometric functions 129—130
Semiderivatives and semiintegrals, tables of, for Heaviside function 131
Semiderivatives and semiintegrals, tables of, for logarithms 130
Semiderivatives and semiintegrals, tables of, for trigonometric and hyperbolic functions 124—125
Semidifferential equations 10 120 157—159
Semidifferential equations for diffusion in planar geometry 201
Semidifferential equations for diffusion in semiinfinite media 197
Semidifferential equations for diffusion in spherical geometry 204
Semidifferential equations for open-circuited finite transmission line 213
Semidifferential equations for short-circuited finite transmission line 213
Semidifferential equations, definition of 157
Semidifferential equations, examples of 157 159
Semidifferential equations, occurrence in electrochemistry 159—160
Semidifferential equations, techniques for solving 157
Semidifferential equations, techniques for solving, Laplace transformation 159
Semidifferential equations, techniques for solving, transformation to ordinary differential equation 157
Semidifferential equations, used to relate current to applied voltage signal in infinite transmission line 212
Semidifferential equations, used to relate electrochemical current to surface concentration 205
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте