|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Girard J.-Y., Taylor P., Lafont Y. — Proofs and Types |
|
|
 |
| Предметный указатель |
For some  see “Existential quantifier” see “Existential quantifier”
Frege 1 2
Function 1 17
Function, Berry order 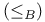 65 65
Function, composition 69
Function, continuous 55 58
Function, fixed point 72
Function, graph 1 66
Function, linear 99 148
Function, not representable 122
Function, on proofs 6 11
Function, on types 83 132 136
Function, partial 60 66
Function, partial recursive 55
Function, pointwise order 66
Function, polynomial resolution 147
Function, provably total 52 123
Function, recursion 50 90 120
Function, representable 52 121
Function, sequential 54
Function, stable 58 62 68
Function, total recursive 122
Function, trace (Tr) 62
Function, two arguments 61
Function-space and implication 12 15 20
Function-space in F 82
Function-space,  -calculus 12 15 -calculus 12 15
Function-space, linear decomposition 101
Function-space, semantics 54 62 64 67 136
functor 59 134 136 141
Gallier 28
Galois theory 134
Gandy 27
Garbage collection 150
GEM 136
General recursion 72
Gentzen 3 28 105
Geometry of interaction 4 160
Girard 30 42 80 82 114 124 150
Goals in PROLOG 112
Godel 1 6 47 54
Godel, 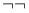 -translation 124 -translation 124
Godel, incompleteness theorem 42 114
Godel, numbering 53
Good elimination 77
Graph, embedding 133 134
Graph, function 1 66
Graph, product 104 138
Graph, web 56
Grothendieck fibration 135 137 141
Hauptsatz (cut elimination) 3 105 151 158
Head normal form 19 52 76 121
Height of a proof (h) 109
Herbrand 4
Hereditarily effective operations 55
Heyting 5 15 80 120
Heyting, arithmetic 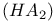 124 124
Horn clause see “Intuitionistic sequent”
Howard see “Curry — Howard isomorphism”
Hyland 133
Hyperexponential function 111
Hypotheses 9
Hypotheses, discharge 9 161
Hypotheses, parcels of 11 36 40 161
Hypotheses, subformula property 76
Hypotheses, variables 11
i see “Introduction”
Idempotence of logic 29
Identification of terms and proofs see “Conversion”
Identity, axiom 30 112 156
Identity, hypothesis 10
Identity, maximal in Berry order 65 135
Identity, polymorphic 83 132 136 138
Identity, proof of 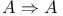 6 6
if see “Casewise definition”
Implication 5
Implication and function-space 12 15 20
Implication, conversion 13
Implication, cut elimination 107
Implication, linear 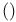 100 153 100 153
Implication, natural deduction, 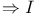 and and  10 10
Implication, realisability 127
Implication, semantics 54
Implication, sequent calculus,  and and 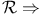 32 32
IN = {0,1,2,...} see “Set of integers”
Inclusion order 56
Incoherence  100 100
Incompleteness theorem 6 42 114 124
Inductive data types 87 121
Inductive definition of +, 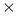 , etc. 50 , etc. 50
Infinite static denotation 2
Infinity (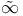 and and  ) 71 ) 71
Initial object 95 152
Input 1 17
Integers 1
Integers in 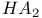 125 125
Integers in F 89 121 147
Integers in T (Int, O, S, R) 48 70
Integers, coherence space, ![$[\Pi X.X\rightsquigarrow(X\rightsquigarrow X)\rightsquigarrow X]$](/math_tex/9c0136abd3442e13f8aab7839ebf1acc82.gif) 147 147
Integers, coherence space, flat (Int) 56 60 66 70
Integers, coherence space, lazy 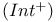 71 98 71 98
Integers, conversion 48
Integers, dI-domain  98 98
Integers, iteration (It) 51 70 90
Integers, linear type (LInt) 148
Integers, normal form 52 121
Integers, realisability (Nat) 126 127
Integers, recursor (R) 48 91
Integers, totality 149
Internalisation 27
Intersection see “Conjunction”
Intersection in [Bool] 140
Intersection, bounded above see “Pullback”
Introduction 8 48
Introduction, 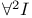 94 125 94 125
Introduction, 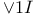 , ,  and and 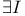 73 73
Introduction, 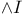 , , 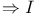 and and 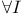 10 10
Introduction, linear logic 161
Introduction, O, S, T and F in T 48
Introduction, pairing and  -abstraction 11 12 19 -abstraction 11 12 19
Introduction, right logical rules 37 40
Introduction, sums 81
Intuitionism 6 150
Intuitionistic sequent 8 30 32 33 112 152
Inversion in linear algebra 101
Isomorphisms 132—134
Iteration (It) 51 70 90
Join see “Disjunction”
Join, preservation (linearity) 99
Joint continuity and stability 61
Jung 133 140
Kleene 123
Konig’s lemma 27
Koymans 133
Kreisel 55
l(t), length of normal form 49
L-domains 140
Lafont 150
Last rule of a proof 8 33
Lazy evaluation 150
Lazy natural numbers 71 98
Least approximant 59 137
Left logical rules see “Sequent calculus”
Lifted sum 96
Limit-colimit coincidence 137
Linear algebra 101
Linear logic 30 35 74 161
Linear logic, Church — Rosser property 159
Linear logic, cut rule 153 156 158
Linear logic, direct product (\&) 61 104 152
| Linear logic, direct sum 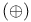 96 103 146 152 96 103 146 152
Linear logic, implication 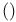 100 104 153 100 104 153
Linear logic, integers (LInt) 148
Linear logic, intuitionistic logic 154
Linear logic, linear maps 99 101
Linear logic, link rule 156
Linear logic, natural deduction 161
Linear logic, negation  100 138 153 100 138 153
Linear logic, notation for tokens 138
Linear logic, of course (!) 101 145 154
Linear logic, polynomial resolution 147
Linear logic, proof nets 155
Linear logic, reducibility 115
Linear logic, semantics 95
Linear logic, sequent calculus 152
Linear logic, sum decomposition 95 103 146
Linear logic, syntax 150
Linear logic, tensor product 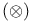 104 146 152 156 104 146 152 156
Linear logic, tensor sum or par 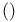 104 152 156 104 152 156
Linear logic, trace (Trlin) 100
Linear logic, units (1,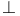 , , 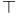 and 0) 104 154 and 0) 104 154
Linear logic, why not (?) 102 154
Link axiom 156
LISTS 47 91
Locally compact space 55
Logical rules 31
Logical rules, cut elimination 105 112
Logical rules, linear logic 153 156
Logical rules, natural deduction 37
Logical view of topology 55
Long trip condition 158
Lowenheim 1 3
Martin — Lof 88
Match (patterns) 81
Maximally consistent extensions 54
Meet see “Conjunction”
Meet, bounded above see “Pullback”
Memory allocation 150
Mod, coherence relation 56
Modalities 101 154
Model theory 3
Modules 17 47
Modus ponens 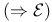 see “Elimination” see “Elimination”
Moggi 141
Nat predicate in 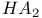 126 126
Natural deduction 8
Natural deduction,  -calculus 11 19 -calculus 11 19
Natural deduction, 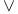 , , 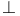 and and  73 73
Natural deduction, 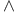 , , 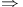 and and 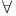 10 10
Natural deduction, conversion 13 20 75 78
Natural deduction, linear logic 161
Natural deduction, normalisation 24 42
Natural deduction, second order 94 125
Natural deduction, sequent calculus 35
Natural deduction, subformula property 76
Natural numbers see “Integers”
Negation 5
Negation,  6 6
Negation, 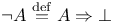 6 73 6 73
Negation, cut elimination 107
Negation, linear  100 138 153 100 138 153
Negation, neg in Bool 50
Negation, sequent calculus 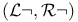 31 31
Neutrality 43 49 116
Nil (empty tree or list) 91
NJ (Prawitz’ system) see “Natural deduction”
Noetherian 66
Nonconvergent rewriting 72
Nondeterminism 150
Normal closure of a field 134
Normal form 18 76
Normal form, cut-free 41
Normal form, existence 24
Normal form, head normal form 19
Normal form, integers 52 121
Normal form, linear logic 159
Normal form, uniqueness 22
Normalisation theorem for F 114
Normalisation theorem for T 49
Normalisation theorem, length of process 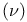 27 43 49 27 43 49
Normalisation theorem, linear logic 155
Normalisation theorem, strong 42
Normalisation theorem, weak 22 24
Not 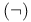 see “Negation” see “Negation”
Object language 10
Ockham’s razor 3
of course (!) 101 138 145 154
Operational semantics 14 121
OR see “Disjunction and parallel or”
Orthogonal 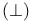 see “Linear negation” see “Linear negation”
Output 17
PA, 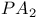 see “Peano arithmetic” see “Peano arithmetic”
Pairing in F 84
Pairing, conjunction 11
Pairing, introduction 19
Pairing, semantics (Pair) 61 68
Par 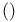 see “Tensor sum” see “Tensor sum”
Parallel or 50 60 70 81
Parallel process 150 159
Parcels of hypotheses 11 36 40 161
Partial equivalence relation 55
Partial function 60
Partial function, coherence space 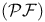 66 66
Partial function, recursive 55
Partial objects 57
Pascal 47
Pattern matching 81
Peano arithmetic (PA) 42 53
Peano arithmetic (PA), second order 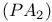 114 123 114 123
Peculiar 134
permutations 134
Pitts 133
Plotkin 56
Plugging 17
Polynomial 148
Positive negative 34 87 139 142
Potential tokens 138
Prawitz 8 80
Predecessor (pred) 51 72 91
Preservation of joins (linearity) 99
Primary equations see “Conversion”
Principal branch or premise 75 76
Product and conjunction 11 15 19
Product in F 84 145
Product, coherence space (\&) 61 68
Product, linear logic ( and \&) 152 and \&) 152
Product, projection 11 61 68 84
Programs 17 53 72 84 124
Projection (embedding) 135 142
PROLOG 28 105 112
proof 5
Proof net 155
Proof of program 53
Proof structure 156
Provably total 53 124
Ptolomeic astronomy 1
Pullback 54 59 61 65 137 141
Quantifiers see “Universal existential
Real numbers 114
Realisability 7
Recursion and iteration 51 70 90
Recursion, recurrence relation 50
Recursion, recursor (R) 48
Recursion, semantics 70
Redex 18 24 48
Reducibility 27 58 123
Reducibility in F 115
Reducibility in T 49
Reducibility,  -calculus 42 -calculus 42
Reduction 18
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




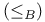
 -calculus
-calculus 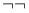 -translation
-translation 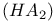
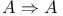
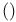
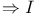 and
and 
 and
and 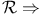

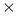 , etc.
, etc. 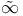 and
and  )
) 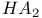
![$[\Pi X.X\rightsquigarrow(X\rightsquigarrow X)\rightsquigarrow X]$](/math_tex/9c0136abd3442e13f8aab7839ebf1acc82.gif)
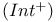

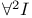
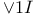 ,
,  and
and 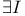
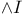 ,
, 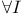
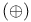

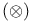
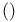
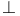 ,
, 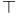 and 0)
and 0) 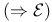
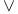 ,
, 
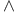 ,
, 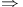 and
and 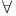

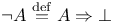
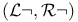
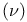
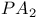
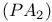
 and \&)
and \&)