|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Girard J.-Y., Taylor P., Lafont Y. — Proofs and Types |
|
|
 |
| Предметный указатель |
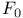 (parallel or) 61 70 (parallel or) 61 70
 see “Existential quantifier” see “Existential quantifier”
 see “Abstraction” see “Abstraction”
 -calculus 12 15 -calculus 12 15
 -calculus, Church — Rosser property 22 -calculus, Church — Rosser property 22
 -calculus, conversion 18 -calculus, conversion 18
 -calculus, head normal form 19 -calculus, head normal form 19
 -calculus, natural deduction 11 19 -calculus, natural deduction 11 19
 -calculus, normalisation 24 42 -calculus, normalisation 24 42
 -calculus, second order polymorphic 82 -calculus, second order polymorphic 82
 -calculus, semantics 54 67 -calculus, semantics 54 67
 -calculus, untyped 19 22 133 -calculus, untyped 19 22 133
 (left logical rules) see “Sequent calculus” (left logical rules) see “Sequent calculus”
 see “Scott” see “Scott”
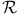 (right logical rules) see “Sequent calculus” (right logical rules) see “Sequent calculus”
 see “System F” see “System F”
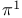 , , 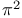 , , 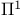 , ,  see “Components” see “Components”
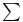 (existential type) in F 86 145 (existential type) in F 86 145
 see “Asymmetrical interpretation” see “Asymmetrical interpretation”
 see “Asymmetrical interpretation” see “Asymmetrical interpretation”
(CR 1—3) see “Reducibility”
0 (zero) see “Integers”
Abramsky i 55
Abstraction 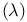 conversion 13 conversion 13
Abstraction 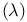 introduction 12 20 introduction 12 20
Abstraction 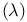 realisability 127 realisability 127
Abstraction 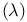 reducibility 45 reducibility 45
Abstraction 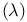 semantics 68 144 semantics 68 144
Abstraction 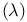 syntax 15 82 syntax 15 82
Absurdity 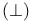 6 95 6 95
Absurdity 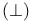 , commuting conversion 78 , commuting conversion 78
Absurdity 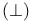 , denotation (f) see “Booleans and undefined object , denotation (f) see “Booleans and undefined object  ” ”
Absurdity 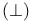 , empty type (Emp and , empty type (Emp and 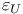 ) 80 ) 80
Absurdity 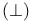 , linear logic (\bot and 0) 154 , linear logic (\bot and 0) 154
Absurdity 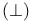 , natural deduction (\bot\mathcal{E}) 73 , natural deduction (\bot\mathcal{E}) 73
Absurdity 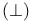 , realisability 129 , realisability 129
Absurdity 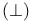 , sequent calculus (\emptyset\vdash\emptyset) 29 , sequent calculus (\emptyset\vdash\emptyset) 29
Ackermann’s function 51
Algebraic domain 56
Alive hypothesis 9
All  see “Universal quantifier” see “Universal quantifier”
Alternations of quantifiers 58 124
Alternative conjunction (\&) see “Direct product”
Amalgamated sum 96 134
Analysis (second order arithmetic) 114
AND see “Conjunction”
Application, conversion 13
Application, elimination 12 20
Application, realisability 127
Application, reducibility 43
Application, semantics (App) 69
Application, stability (Berry order) 65
Application, syntax 15 82
Application, trace formula (App) 63 64 144
Approximation of points and domains 57 134
Arrow type see “Implication and function-space”
Associativity of sum type 98
Asymmetrical interpretation 34
Atomic formulae 4 5 30 112 160
Atomic points see “Tokens”
Atomic sequents 112
Atomic types 15 48
Automated deduction 28 34
Automorphisms 134
Axiom, comprehension 114 118 123
Axiom, excluded middle 6 156
Axiom, hypothesis 10
Axiom, identity 30
Axiom, link 156
Axiom, proper 112
Bad elimination 77
Barendregt 22
Berry 54
Berry order  65 66 135 146 65 66 135 146
Beta 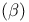 rule see “Conversion” rule see “Conversion”
Binary completeness 56
Binary trees (Bintree) 93
Binding variables 5 12 15 83 161
Boole 3
Booleans 4
Booleans in F  84 140 84 140
Booleans in system F 84
Booleans in T (Bool, T, F) 48 50 70
Booleans, coherence space, ![$[\Pi X.X\rightarrow X\rightarrow X]$](/math_tex/b2f32ffb73c3783e0426261a9753837f82.gif) 140 140
Booleans, coherence space, Bool 56 60 70
Booleans, commuting conversion 86
Booleans, conversion 48
Booleans, denotation (t and f) 4
Booleans, totality 149
Bounded meet see “Pullback”
Boundedly complete domains 140
Brouwer 6
By values 51 70 91 133
C, C? see “Contraction”
Camembert 3
CAML 81
Candidate, reducibility 43 115 116
Candidate, totality 58 149
Cantor 1
Cartesian closed category 54 62 67 69 95 152
Cartesian natural transformation see “Berry order”
Cartesian product see “Product”
Casewise definition (D) 48 83 97
Category 59 95 133 135
Characteristic subgroup 134
Church — Rosser property 16 22 49 74 79 90 114 152 159
CLIQUE 57 62 101 138
Closed normal form 19 52 121
Coclosure 135
Coherence space 56
Coherence space,  types 143 types 143
Coherence space, booleans, ![$[\Pi X.X\rightarrow X\rightarrow X]$](/math_tex/b2f32ffb73c3783e0426261a9753837f82.gif) 140 140
Coherence space, booleans, Bool 56 60 70
Coherence space, coherence relation 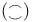 56 56
Coherence space, direct product (\&) 62
Coherence space, direct sum 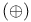 96 103 96 103
Coherence space, empty type 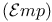 104 139 104 139
Coherence space, function space (\rightarrow) 64 102 138
Coherence space, integers ![$[\Pi X.X\rightarrow X\rightarrow X]$](/math_tex/b2f32ffb73c3783e0426261a9753837f82.gif) 147 147
Coherence space, integers flat (Int) 56 60 66 70
Coherence space, integers lazy 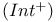 71 98 71 98
Coherence space, linear implication 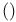 100 104 138 100 104 138
Coherence space, linear negation  100 138 100 138
Coherence space, of course (!) 101 138 145
Coherence space, Pair, 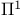 , ,  68 68
Coherence space, partial functions 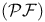 66 66
Coherence space, semantics 67 132
Coherence space, singleton (Sgl) 104 139
Coherence space, tensor product 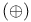 104 138 104 138
Coherence space, tensor sum or par 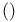 104 104
Coherence space, tokens and web 56
Coherent or spectral space 56
Collect (forming trees) 94
Communicating processes 155
Commutativity of logic 29
Commuting conversion of sum see “Conversion”
Compact 59 66
Compact-open topology 55
Complementary graph see “Linear negation”
Complete subgraph see “Clique”
Complexity, algorithmic 53 111 143
Complexity, logical 42 58 114 122 124 140
Components (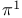 and and 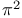 ), elimination 19 ), elimination 19
Components (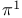 and and 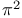 ), reducibility 43 ), reducibility 43
Composition, stable functions 69
Comprehension scheme 114 118 123 126
Computational significance 1 11 17 112 120
Confluent relation see “Church — Rosser property”
Conjunction 5
Conjunction and product 11 15 19
| Conjunction, conj in Bool 50
Conjunction, conversion 13
Conjunction, cut elimination 105
Conjunction, in F: $\Pi X.(U\rightarrow V\rightarrow X)\rightarrow X 84
Conjunction, linear logic 152
Conjunction, natural deduction,  , ,  and and  10 10
Conjunction, realisability 126
Conjunction, sequent calculus,  , ,  and and  31 31
Cons (add to list) 91
Consistency, equational 16 23 152
Consistency, logical (consis) 42 114 124
Constants by vocation 60 66
Constructors see “Data types in F”
Continuity 54 59 137
Contraction,  and and  29 29
Contraction, linear logic (C?) 154
Contractum 18 (see also “Redex”
Control features of PROLOG 28
Conversion  18 18
Conversion  in F 83 94 in F 83 94
Conversion  , ,  -calculus 11 16 18 69 -calculus 11 16 18 69
Conversion  , bogus example 75 , bogus example 75
Conversion  , booleans (D) 48 , booleans (D) 48
Conversion  , commuting 74 78 85 97 103 , commuting 74 78 85 97 103
Conversion  , conjunction , conjunction 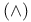 13 13
Conversion  , degree 25 , degree 25
Conversion  , denotational equality 69 132 , denotational equality 69 132
Conversion  , disjunction , disjunction  75 97 75 97
Conversion  , existential quantifier , existential quantifier  75 75
Conversion  , implication (\Rightarrow) 13 , implication (\Rightarrow) 13
Conversion  , infinity (\infty) 72 , infinity (\infty) 72
Conversion  , integers (R, It) 48 51 , integers (R, It) 48 51
Conversion  , linear logic (proof nets) 158 , linear logic (proof nets) 158
Conversion  , natural deduction 13 20 , natural deduction 13 20
Conversion  , reducibility 43 116 , reducibility 43 116
Conversion  , rewrite rules 14 , rewrite rules 14
Conversion  , second order 94 , second order 94
Coquand 116 133
Correctness criterion for proof nets 158
Correctness criterion for tokens of IT types 139 142
Couple (forming trees) 93
Cumulative conjunction see “Tensor product”
Curry — Howard isomorphism 5 150
Curry — Howard isomorphism, conjunction and product 14
Curry — Howard isomorphism, disjunction and sum 80
Curry — Howard isomorphism, implication and functions 14
Curry — Howard isomorphism, none in sequent calculus 28
Curry — Howard isomorphism, second order 94
Cut rule, Cut 30
Cut rule, elimination of 3 105 151 158
Cut rule, linear logic 153 156 158
Cut rule, natural deduction 35 40
Cut rule, not Church — Rosser 150
Cut rule, proofs without 33 159
Cut rule, restriction of 112
D,  see “Casewise definition” see “Casewise definition”
Data types in F 87 89
Dead hypothesis 9
Deadlock 155
Deduction (natural) 9
Degree 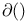 , of formula or type 24 109 , of formula or type 24 109
Degree d(), of cut or redex 24 109
Delin see “Linearisation”
Denotation 1
Denotational semantics 14 54 67 95 132
Dereliction (D?) 154
dI-domains 71 98
Direct product (\&), coherence space 61 67
Direct product (\&), linear logic 152
Direct sum 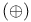 , coherence space 96 103 146 , coherence space 96 103 146
Direct sum 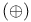 , coherence space, example 66 , coherence space, example 66
Direct sum 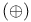 , linear logic 152 , linear logic 152
Directed joins 57 59 66
Discharge 9 12 37 73 161
Discrete graph see “Flat domain”
Disjunction 5 6 95
Disjunction and sum 81
Disjunction, commuting conversion 78
Disjunction, conversion 75
Disjunction, cut elimination 106
Disjunction, disj in Bool 50
Disjunction, intuitionistic  32 32
Disjunction, intuitionistic property 8 33
Disjunction, linear logic ( and and  ) 152 ) 152
Disjunction, natural deduction  , ,  and and  73 73
Disjunction, sequent calculus  , ,  and and  31 31
Domain theory 56 132
Domain theory, dI-domains 71 98
Domain theory, domain equations 98
Domain theory, Girard versus Scott 54 66 98
Domain theory, L-domains 140
Domain theory, lifted sum 96
Donkey 134
Dynamic 2 14 54
Elimination 8 48
Elimination,  94 125 94 125
Elimination,  , ,  and and  73 73
Elimination,  , ,  , ,  and and  10 10
Elimination, application and components 19
Elimination, good and bad 77
Elimination, left logical rules 37 40
Elimination, linear logic 161
Elimination, linearity of 99 103
Elimination, R and D in T 48
Embedding-projection pair 133 134
Empty type and absurdity 80
Empty type in F:  85 139 85 139
Empty type, coherence space 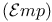 95 104 139 95 104 139
Empty type, Emp and 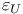 80 80
Empty type, linear logic (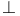 and 0) 154 and 0) 154
Empty type, realisability 129
Equalisers 137
Equations between terms and proofs see “Conversion”
Espace coherent 56
Eta rule see “Secondary equations”
Evaluation see “Application”
Event structures 98
Exchange,  and and  29 29
Exchange, linear logic (X) 153
Existential quantifier 5 6
Existential quantifier, commuting conversion 78
Existential quantifier, conversion 75
Existential quantifier, cut elimination 108
Existential quantifier, intuitionistic property 8 33
Existential quantifier, natural deduction,  and and  73 73
Existential quantifier, sequent calculus,  and and  32 32
Existential type in F  86 145 86 145
Exponential object see “Implication and function-space”
Exponential process see “Complexity algorithmic”
Expressive power 50 89 155
Extraction see “Universal application”
F (Girard — Reynolds system), representable functions 120
F (Girard — Reynolds system), semantics 132
F (Girard — Reynolds system), strong normalisation 42 114
F (Girard — Reynolds system), syntax 82
False denotation $(f,\mathcal{F},F) see “Booleans”
False proposition 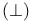 see “Absurdity” see “Absurdity”
feasible see “Complexity algorithmic”
Fields of numbers 134
Filtered colimits 59 137
Finite approximation 57 66 132 134
Finite branching tree 27
Finite normalisation 24
Finite points  57 57
Finite presentability 66
Finite, sense and denotation 2
Finite, very 59 66
Fixed point 72 95
Flat domain 57 60 66 70 140
For all  see “Universal quantifier” see “Universal quantifier”
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



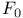 (parallel or)
(parallel or) 

 (left logical rules)
(left logical rules) 
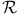 (right logical rules)
(right logical rules) 
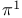 ,
, 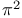 ,
, 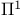 ,
, 
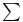 (existential type) in F
(existential type) in F 

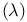 conversion
conversion 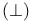
 ”
”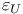 )
) 

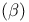 rule
rule 
![$[\Pi X.X\rightarrow X\rightarrow X]$](/math_tex/b2f32ffb73c3783e0426261a9753837f82.gif)
 types
types 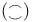
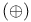
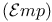
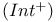
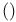

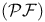
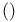
 ,
,  and
and 
 ,
,  and
and 
 and
and 

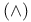



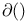 , of formula or type
, of formula or type 
 and
and  )
)  ,
,  and
and 
 and
and 

 and
and 
 and
and 

 and 0)
and 0)  and
and 
 and
and  and
and 

