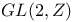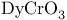|
Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета |
| Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск |
© Электронная библиотека попечительского совета мехмата МГУ, 2004-2025 |
|
О проекте |
|
О проекте
|




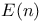
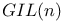
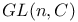
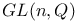
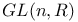
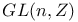
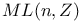
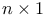 matrix = column matrix consisting of n elements
matrix = column matrix consisting of n elements 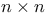 matrix = matrix consisting of n rows and n columns
matrix = matrix consisting of n rows and n columns 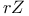 -Bravais class of (3+1)-dimensional point lattices
-Bravais class of (3+1)-dimensional point lattices 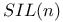
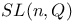
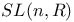
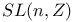

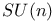
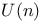

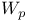 -symmetry groups
-symmetry groups 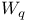 symmetry groups
symmetry groups 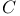 = set of all complex numbers
= set of all complex numbers 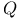 = set of all rational numbers
= set of all rational numbers 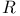 = set of all real numbers
= set of all real numbers 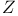 = set of all integers (positive, zero, and negative)
= set of all integers (positive, zero, and negative) 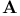 -groups of space-time rotations
-groups of space-time rotations 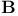 -groups of space-time rotations
-groups of space-time rotations 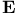 -groups of space-time rotations
-groups of space-time rotations 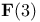 -class of (3+1)-dimensional superspace groups
-class of (3+1)-dimensional superspace groups 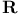 -equivalent matrix groups
-equivalent matrix groups 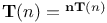
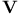
 isomorphism
isomorphism 
 \gamma$
\gamma$ 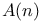

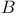 -equivalent groups of isometries where 3 is a subgroup of an affine group
-equivalent groups of isometries where 3 is a subgroup of an affine group 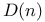


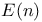


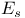


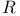


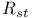
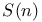
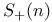
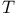
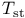
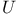 -groups of space-time rotations
-groups of space-time rotations 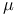 -group of rotations
-group of rotations 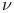 -group of rotations
-group of rotations 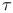 -group of rotations
-group of rotations