|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Opechowski W. — Crystallographic and metacrystallographic groups |
|
|
 |
| Предметный указатель |
Symmetry group of a modulated point lattice 540
Symmetry group of a plane 161
Symmetry group of a point lattice 218
Symmetry group of a point set 191
Symmetry group of a simple crystal 299
Symmetry group of a static homogeneous electromagnetic field T14.2
Symmetry group of an extended modulated point lattice 542 546 548
Symmetry group of the constitutive relations 397
Symmetry groups of vector functions constant in space and time 392 T14.2
Symmetry of electric and magnetic fields N14.2
Symmetry operation N7.3
Symmetry, higher 192
Symmetry, lower 192
Symmetry, opposite 193
Symmetry, some 192
Symmetry, the same 193
Symmorphic line group 325
Symmorphic space group 255 270 N9.3
Syngony Npr
System of Bravais classes of lattice groups 239 240
System of Bravais classes of point lattices 239 240
System of Bravais flocks (= Bravais-flock systems) of arithmetic classes of finite integral matrix groups 239 240
System of geometric classes (= geometric-class system) of crystallographic groups of rotations 262 T6.2 T6.7
System of geometric classes of space groups (= ITC system) 278
System of lattice groups 239
System of point lattices 239
System of proper affine classes of Bravais space groups 239 240
System of proper arithmetic classes of Bravais groups 240
Systems of space groups, Bravais, = Bravais-flock systems of space groups 277
Systems of space groups, ITC, = systems of geometric classes of space groups 277
Systems of space groups, NWB, = systems of the third kind 278 279
t-dimensional lattice group of an n-dimensional Euclidean point space 195
T-subgroup of a space group 260 436 437
T-subgroups of the Bravais space group Cmmm T9.2.1
T-supergroup of a space group 260
Tetragonal Bravais system of point lattices T8.3
Tetragonal Bravais system of space groups T9.2.2
Tetragonal geometric-class system of groups of rotations T6.2 T6.5
Tetragonal group of proper rotations 155 T6.2 T6.5
Tetragonal point lattice, body-centred 244
Tetragonal point lattice, primitive 244
Tetrahedral group of proper rotations 155 T6.2 T6.5
Theorem on invariant vectors of a representation 139
Theorem on the direct product of representations of a group 145
Three-dimensional Euclidean point space (ordinary space) 87 101 148
Three-dimensional line group 315
Time (one-dimensional Euclidean point space) 87 101 165
Time group 165 529
Time inversion 165
Time-independent function 388
Time-inversion group 165
Time-inversion in quantum mechanics 531
Time-inversion operator 532
Time-translation group 165
Trace of a matrix 76
Transform of a permutation by another permutation 31 34
Transform of an element of a group 26
Transform of an element of a group by an automorphism of the group 45
Transformation of a set onto itself = permutation of a set 5 30
Transforming away the translational part of an affine transformation 119 151
Transition probability 521
Transitive group of permutations 39 68
Transitive relation 6
Transitive set 39
Translation component of a rigid motion N4.4
Translation of an affine space 111 113
Translation subgroup of the affine group 111
Translation-equivalent subgroup = T-subgroup 260
Translational part of an affine transformation 113 117 128
Translational part of an isometry 117 128 N4.4
Transpose of a matrix 76
Triclinic Bravais system of point lattices T8.3
Triclinic Bravais system of space groups T9.2.2
Triclinic geometric-class system of groups of rotations T6.2 T6.5
Triclinic groups of rotations T6.2 T6.5
| Triclinic ITC-system of space groups T9.2.2
Triclinic point lattice 244
Trigonal Bravais system (= rhombohedral Bravais system) of point lattices 244 T8.3
Trigonal Bravais system of point lattices T8.3
Trigonal Bravais system of space groups T9.2.3
Trigonal geometric-class system of groups of rotations T6.2 T6.5
Trigonal groups of rotations T6.2 T6.5
Trigonal ITC-system (= rhombohedral ITC-system) of space groups T9.2.3
Trigonal point lattice = rhombohedral point lattice 244
Trivial extension (= split extension) of a group 59
Trivial group 11 15
Trivial magnetic group 402
Trivial metacrystallographic group 352
Trivial representation of a group 24
Trivial spin group 506
Trivial subgroup 15
Two-colour group = black and white group 357 374
Two-colour group corresponding to a magnetic group 375 406
Two-dimensional Euclidean point space 162
Two-sided band group 331
Two-sided line group 331
Two-sided line strip 330
Type of point lattices = Bravais class of point lattices N8.7
Type of space groups = space-group type 264
Unimodular matrix 79 109
Union of sets 4
Unit cell of a point lattice 210 N8.2
Unit cell of a point set generated by a line group 328
Unit cell of a simple crystal 292
Unit element (= identity element) of a group 10
Unit ray 519
Unit vector 520
Unitary group of a complex vector space 526
Unitary matrix 76
Unitary matrix group U(n) 77
Unitary transformations of a vector space 527
Unitary vector space 520
Unitary vector space associated with an atomic system 522
Unitary-antiunitary group of a complex vector space 527
Unprimed elements of a magnetic group 402
Unprimed elements of the Newton group 168
Unprimed subgroup of a magnetic group 405
Unprimed subgroup of a subgroup of the Newton group 168 169
Unprimed subgroup of the Newton group 168
V 88
V(n) 89
Vector 88
Vector addition 88
Vector functions 387 389
Vector group = spin group 354 359 503 504 505
Vector space 8
Vector space over a field 88
Vector space over the field 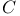 of complex numbers = complex vector space 88 of complex numbers = complex vector space 88
Vector space over the field 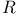 of real numbers = real vector space 88 of real numbers = real vector space 88
Vector space regarded as an Abelian group 88
Vector space, n-diinensional 89
Vector W-group 355
Vector-space component of a Euclidean point space 98
Vector-space component of an affine point space 92
Vector-valued functions: one-, two-, and three-dimensional 354 505 506
Vierergruppe = four-group 11 166
Voronoi domain = Voronoi polyhedron N8.8
Wigner — Seitz cell N8.8
Wigner's Theorem N21.3
Wild automorphism of the field of complex numbers 52 523
Wreath product 57 355 383
Wyckoff 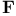 -class 294 N10.2 -class 294 N10.2
Wyckoff class of simple crystals = Wyckoff position for a space group 293 294 295 T10.2
Wyckoff classification of simple crystals 293
Wyckoff letter 293
Wyckoff notation 293
Wyckoff position for a space group = Wyckoff class of simple crystals 295
Zassenhaus' algorithm 275
Zellengleiche Untergruppe = T-subgroup 261
Zero-vector = null-vector 88
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



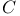 of complex numbers = complex vector space
of complex numbers = complex vector space 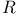 of real numbers = real vector space
of real numbers = real vector space 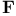 -class
-class